Главная

Лекция 1. Введение в сопротивление материалов

Содержание

Задачи и методы сопротивления материалов

Реальный объект и расчетная схема

Связи и опорные устройства

Внешние и внутренние силы. Метод сечений

Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

Допущения, применяемые в сопротивлении материалов

Напряжения

Перемещения и деформации

Закон Гука и принцип независимости действия сил

Общие принципы расчета конструкции

Вопросы для самопроверки

Тесты для самоконтроля

Задачи и методы сопротивления материалов

Сопротивление материалов - наука об инженерных методах расчета на прочность, жесткость и устойчивость типовых элементов сооружений и деталей машин.

Из большого разнообразия элементов сооружений и машин в данном курсе рассматриваются наиболее простые, часто встречающиеся элементы, которые схематизируются и сводятся к типовым расчетным схемам.

Элементы сооружений отличаются друг от друга формами, размерами, материалом, функциональным назначением, рядом специальных требований. При этом следует отметить, что все без исключения элементы как искусственного, так и естественного происхождения обладают такими свойствами, как прочность и жесткость, то есть способностью, не разрушаясь воспринимать различные нагрузки и сопротивляться изменению своих первоначальных форм и размеров, без чего не может нормально функционировать сооружение. Цель расчетов в сопротивлении материалов – создание прочных, устойчивых, обладающих достаточной жесткостью, долговечностью и вместе с тем экономичных элементов сооружений

Например, конструкции стропильной фермы, междуэтажных перекрытий зданий должны выдерживать нагрузки от атмосферных воздействий, оборудования и людей и обладать достаточной жесткостью, обеспечивающей ограничение прогибов для создания нормальных условий функционирования сооружения.

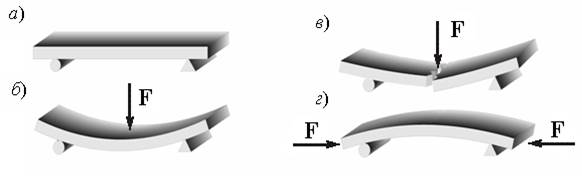
Рис. 1. Характер деформирования и разрушения стержня под нагрузкой:

а) – элемент до нагружения; б) – деформация стержня при изгибе; в) – вид излома элемента при изгибе; г) – изгиб стержня при сжатии

Существуют и другие разделы механики деформированного твердого тела. Теория упругости изучает напряженное и деформированное состояния твердого упругого тела (бруса, конструктивного элемента) вызванные силовыми и температурными воздействиями. Аналогичными вопросами занимается и спопротивление материалов. Однако теория упругости решает свои задачи более общими и точными методами, применяя сравнительно сложный математический аппарат. К теории упругости близко примыкает теория пластичности.

Теория пластичности изучает закономерности образования напряжений и деформаций, возникающих на стадии пластического деформирования тела (бруса, конструктивного элемента).

Теория упругости и пластичности имеют два основных назначения: 1) оценка точности и переделов применимости решений задач, полученныхметодами сопротивления материалов; 2) решение таких задач, которые не могут быть решены методами сопротивления материалов (расчет пластин, оболочек, балок-стенок, массивных тел и др.).

Относительно новой ветвью механики сплошных деформируемых сред является теория ползучести (вязкоупругости). Свойство ползучести материалов состоит в том, что даже при постоянных нагрузках напряжения и деформации в материале (брусе, конструктивном элементе) изеняются во времени. Изменение во времени деформаций нагруженного образца или конструктивного элемента называется ползучестью. Например, вследствие ползучести диска и лопаток газовой турбины могут перекрываться зазоры между лопатками и корпусом, что приведет к разрушению лопаток. Изменение во времени напряжений деформированного образца или элемента конструкции называется релаксацией. Так, за счет релаксации напряжений в болтах фланцевого соединения может нарушаться герметичность паропровода.

Прочностные и жесткостные качества элементов сооружений зависят от многих факторов: материала, размеров, характера возникающих деформаций и др. Металлические конструкции обладают большей прочностью и жесткостью, чем аналогичные деревянные конструкции. Стержень из одного и того же материала, имеющий большие поперечные размеры, более прочный и жесткий, при этом его легче разрушить, изгибая, чем растягивая. Тонкий стержень при его сжатии разрушается в результате выпучивания в поперечном направлении, в то же время это явление отсутствует при продольном растяжении и для разрушения стержня требуется значительно большая нагрузка.

Например, возьмем деревянный брусок (рис.1, а). Начнем сгибать стержень. Чем сильнее мы будем прикладывать усилия, тем больше он изогнется (рис.1 б), и при какой то величине усилий сломается (рис.1, в). Подведя итог можно утверждать, что всякое реальное тело под воздействием сил меняет свою форму и размеры, т. е. деформируется. Деформации обуславливают появление внутри элемента сил сопротивления. Если внешние силы больше сил сопротивления, происходит разрушение элемента сооружения.

При возрастании нагрузки выше определенных значений в теле наряду с упругими будут возникать деформации не исчезающие после снятия нагрузки. Такие деформации называются остаточными. Возникновение остаточных деформаций, наравне с разрушением связано с нарушением нормальной работы конструкции и, как правило, недопустимо.

Способность конструкции воспринимать заданную нагрузку, не разрушаясь и без остаточных деформаций, называют прочностью.

Все элементы сооружения, из каких бы материалов они ни были изготовлены, под нагрузкой деформируются. Однако значительные деформации могут мешать нормальной эксплуатации сооружения.

Способность сооружений и ее частей под нагрузкой сохранять свои размеры и форму в установленных нормами пределах называется жесткостью.

Рассмотрим еще один пример. Будем сжимать тонкий и длинный стержень (тот же деревянный брусок). Уже при незначительной силе стержень изогнется, как показано на рис.1, г. В этом случае первоначальная форма прямолинейная форма равновесия стержня становится неустойчивой.

Способность конструкции, и ее частей, сохранять под нагрузкой первоначальную форму упругого равновесия называется устойчивостью.

Обычно потеря устойчивости сопровождается мгновенным изменением формы элемента и разрушением конструкции.

Методами сопротивления материалов выполняются расчеты, на основании которых определяются необходимые размеры деталей машин и конструкций инженерных сооружений. Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.

Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.

Ресурс – допустимый срок службы изделия. Указывается в виде общего времени наработки или числа циклов нагружения конструкции.

Отказ – нарушение работоспособности конструкции.

Опираясь на вышесказанное, можно дать определение прочностной надежности.

Прочностной надежностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции.

Надежность конструкции обеспечивается, если она сохраняет прочность, жесткость и устойчивость при гарантированной долговечности. Ее экономичность в значительной мере определяется расходом материала, применением менее дефицитных конструкционных материалов, возможностью изготовления деталей по наиболее прогрессивным технологиям. Надежность и экономичность - противоречивые требования.

В сопротивлении материалов широко применяются методы теоретической механики и математического анализа, используются данные из разделов физики, изучающих свойства различных материалов, материаловедения и других наук. К тому же сопротивление материалов является наукой экспериментально-теоретической, так как она широко использует опытные данные и теоретические исследования.

В отличие от теоретической механики сопротивление материалов рассматривает задачи, в которых наиболее существенными являются свойства твердых деформируемых тел, а законами движения тела как жесткого целого здесь пренебрегают. В теоретической механике рассматривают равновесие абсолютно твердого (недеформированного) тела, при составлении уравнений равновесия допустимы замена системы сил статически эквивалентной системой, перенос сил вдоль линии их действия, замена ряда сил их равнодействующей. При решении задач сопротивления материалов, подобные замены или перенос сил недопустимы.

В то же время, вследствие общности основных положений, сопротивление материалов рассматривается как раздел механики твердых деформируемых тел. В состав механики деформируемых тел входят также такие дисциплины, как: теория упругости, теория пластичности, теория ползучести, теория разрушения и др., рассматривающие, по существу, те же вопросы, что и сопротивление материалов. Различие между сопротивлением материалов и другими теориями механики твердого деформируемого тела заключается в подходах к решению задач.

Строгие теории механики деформируемого тела базируются на более точной постановке проблем, в связи с чем, для решения задач приходится применять более сложный математический аппарат и проводить громоздкие вычислительные операции. Вследствие этого возможности применения таких методов в практических задачах ограничены.

В свою очередь, методы сопротивления материалов базируются на упрощенных гипотезах, которые, с одной стороны, позволяют решать широкий круг инженерных задач, а с другой, получать приемлемые по точности результаты расчетов.

При этом главной задачей курса является формирование знаний для применения математического аппарата при решении прикладных задач, осмысления полученных численных результатов и поиска выбора наиболее оптимальных конструктивных решений. Конечная цель науки сопротивления материалов – определение размеров элементов сооружений, обеспечивающих его работоспособность при минимальном расходе материалов. То есть данный предмет является базовым для формирования инженерного мышления и подготовки кадров высшей квалификации по техническим специализациям.

Сопротивление материалов является основой для изучения курса «Детали машин» и различных специальных дисциплин, таких, как «Конструкция и прочность двигателей», «Конструкция и прочность летательных аппаратов» и т.п.

Зарождение науки о сопротивлении материалов относится к XVII в. и связано с работами знаменитого ученого того времени Галилео Галилея. Значительный вклад в ее развитие был сделан выдающимися учеными: Гуком, Бернулли, Сен-Венаном, Коши, Ламе, Эйлером и др. В России в конце XIX-начале XX века важные исследования в области сопротивления материалов провели русские ученые Д.И.Журавский, Ф.С.Ясинский, И.Г.Бубнов, С.П.Тимошенко и др.

Реальный объект и расчетная схема

В сопротивлении материалов, как и во всякой отрасли естествознания, исследование вопроса о прочности или жесткости реального объекта начинается с выбора расчетной схемы. Расчетная схема конструкции - его упрощенная схема, освобожденная от несущественных в данной задаче особенностей. К числу существенных факторов расчетной схемы относят: геометрию объекта, его форму и размеры; физические характеристики материала; нагрузки, прикладываемые к объекту. Например, при расчете на прочность троса, поднимающего груз, можно не учитывать форму груза, сопротивление воздуха, изменение давления и температуры воздуха с высотой, силу тяжести троса и многие другие факторы, учет которых усложняет расчет троса, но практически не влияет на конечный результат. Трос, свитый из большого числа тонких проволочек, в данном примере можно рассматривать как однородный стержень круглого поперечного сечения, нагруженный растягивающей силой, сосредоточенной в месте крепления груза.

При выборе расчетной схемы вводятся упрощения (схематизация) реального объекта, т.е. отбросить все те факторы, которые не могут сколько-нибудь заметным образом повлиять на работу системы в целом.

Рис.2. Приведение реального объекта к расчетной схеме

Такого рода упрощения задачи совершенно необходимы, так как решение с полным учетом всех свойств реального объекта является принципиально невозможным в силу их очевидной неисчерпаемости.

Основным упрощающим приемом в сопротивлении материалов является приведение геометрической формы тела к схемам бруса (стержня), оболочки или пластины. Как известно, любое тело в пространстве характеризуется тремя измерениями.

Под стержнями подразумеваются тела довольно разнообразной и вместе с тем специфической формы. Представим себе некоторую линию, вдоль которой движется плоская фигура так, что её центр тяжести находится на этой линии, а плоскость фигуры нормальна к ней (рис. 3). Если размеры фигуры b, h существенно меньше длины линии l, то описанное указанным образом тело называется стержнем (или брусом); соответственно отмеченная плоская фигура называется поперечным сечением стержня, а отмеченная линия – осью стержня.

Рис. 3. Прямой брус (стержень) постоянного сечения

Если поперечное сечение при движении вдоль оси не изменяется, то тогда имеет место стержень постоянного сечения; в противном случае – стержень переменного сечения. Если ось стержня – прямая линия, то это прямой стержень. Если ось стержня – кривая линия, то его называют кривым стержнем. Если поперечное сечение при движении вдоль оси вращается вокруг касательной к оси, то стержень называют естественно-закрученным. Примером прямого естественно-закрученного стержня постоянного сечения является рабочая часть сверла. Используются также и другие названия. В частности, брус, работающий на растяжение, называют стержнем (рис.4, а), на изгиб, обычно называют балкой, а стержень, передающий вращательное движение, – валом. Стержневые элементы, воспринимающие вертикальные сжимающие силы, называют стойками, а наклонные элементы - раскосами. Конструкцию, состоящую из соединенных изгибаемых стержней, называют рамой. Если же благодаря шарнирному соединению стержней все они работают только на растяжение или сжатие (от нагрузки, приложенной в узлах), то конструкцию называют фермой.

Второй основной геометрической формой, рассматриваемой в сопротивлении материалов, является оболочка, под которой подразумевается тело, у которого одно из измерений (толщина) намного меньше, чем два других (рис.4, в). К оболочкам относятся различного рода резервуары, котлы, купола зданий, корпуса подводных лодок, обшивка фюзеляжа самолета и т.п.

Срединная поверхность – это геометрическое место точек, равноудаленных от внешней и внутренней поверхностей оболочки.

Оболочка, срединная поверхность которой представляет собой плоскость, называется пластиной (рис.4, б). Примером могут служить крыши и днища резервуаров, перекрытия зданий, различные диски и т.п.

Элемент конструкции, размеры которого во всех направлениях мало отличаются друг от друга, называется массивом. К ним относятся фундаменты сооружений, подпорные стенки и т.п.

Методы расчета пластин, оболочек и массивных тел при больших деформациях рассматриваются в курсе «Прикладная теория упругости». Способы расчета стержневых систем изучаются в курсе «Строительная механика».

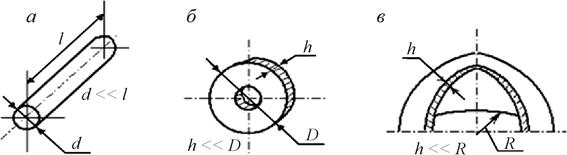
Рис. 4. Основные модели формы в моделях прочностной надежности:
а – стержень; б – пластина; в – оболочка

В заключение отметим, что если для одного объекта может быть предложено несколько расчетных схем, то, с другой стороны, одной расчетной схеме может быть поставлено в соответствие много различных реальных объектов.

Последнее обстоятельство является весьма важным, так как исследуя некоторую схему, можно получить решение целого конкретных задач, сводящихся к данной схеме.

Связи и опорные устройства

Для соединения отдельных частей конструкции между собой и передачи внешней нагрузки на основание на нее накладываются связи, ограничивающие перемещения тех точек сооружения, к которым они приложены. Связи могут ограничивать либо повороты точек сооружения, либо их линейные смещения, либо и то и другое.

Основным видом связей в расчетной схеме является шарнирная связь.

Простой шарнир (рис. 5) накладывает две связи.

Рис. 5

В расчетную схему входит основание, т.е. тело, на котоpое опирается cистема в целом, считающееся неподвижной.

Неподвижность расчетной схемы относительно основания обеспечивается опорными связями (опорами).

Все опорные связи условно делятся на три основных типа:

- Подвижная шарнирная опора (рис.6, а). Такая опора не препятствует вращению конца бруса и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через ось катка (R).

- Неподвижная шарнирная опора (рис.6, б). Такая опора допускает вращение конца бруса, но устраняет поступательное движение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие, одна из которых направлена вдоль оси бруса (Н), другая - перпендикулярно к оси бруса (R).

- Жесткая заделка или защемление (рис.6, в). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре в общем случае может возникать реакция, которую обычно раскладывают на две составляющие (H и R) и момент защемления (М).

При рассмотрении реального объекта в число внешних сил включаются не только заданные нагрузки, но и реакции связей (опор), дополняющие систему сил до равновесного состояния.

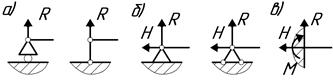
Рис. 6

Внешние и внутренние силы. Метод сечений

Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называются внешними. Внешние силы, действующие на тело, можно разделить на активные (независимые) и реактивные. Реактивные усилия возникают в связях, наложенных на тело, и определяются действующими на тело активными усилиями.

По способу приложения внешние силы делятся на объемные и поверхностные.

Объемные силы распределены по всему объему рассматриваемого тела и приложены к каждой его частице. В частности, к объемным силам относятся собственный вес сооружения, магнитное притяжение, сила тяжести или силы инерции. Единицей измерения объемных сил является сила, отнесенная к единице объема - кН/м³.

Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рассматриваемого объекта с окружающими телами (давление ветра, воды на стенку).

В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки подразделяются на сосредоточенные и распределенные.

Если давление q₁ (Н/м²) передается на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента (a≪l), то его на основании принципа Сен-Венана можно привести к сосредоточенной силе F (рис. 7). Например, воздействие колонн на фундаментную плиту достаточно больших размеров можно рассматривать как действие на нее сосредоточенных усилий.

Сосредоточенная сила F измеряется в ньютонах (Н), килоньютонах (кН). Подобным образом вводятся понятия сосредоточенных изгибающих и крутящих моментов.

Рис. 7

Если давление q₂ (Н/м²) передается на элемент конструкции через площадку, размеры которой сравнимы с размерами всего элемента (c<l), то его представляют в виде распределенной или погонной нагрузки q₃ с размерностью кН/м или кН/м² (рис. 7). Примером может служить собственный вес балки, действие снеговой или ветровой нагрузки на сооружение, давление жидкости в резервуаре. Распределенная нагрузка может действовать и по линии как, например, при соприкасании двух цилиндров при параллельном расположении их осей.

На расчетной схеме вместо бруса изображается его ось. Нагрузки, распределенные по линии и сосредоточенные в точках, реально не существуют. Их можно получить лишь в результате схематизации реальных нагрузок, распределенных по объему (объемных сил) и по поверхности.

По времени действия внешние нагрузки (силы) разделяются на постоянные и временные. Собственный вес зданий – это постоянно действующая нагрузка на протяжении всего периода эксплуатации здания; поезд, идущий через мост, - это нагрузка временная.

По характеру изменения силы во времени различают нагрузки статические и динамические. Статические нагрузки (постоянные) - такие, которые изменяют свою величину или точку приложения (направление) с очень небольшой скоростью, так что возникающими при этом ускорениями (силами инерции) можно пренебречь. Динамические нагрузки - изменяются во времени с большой скоростью, при этом силы инерции должны быть учтены, так как оказывают существенное влияние на конструкцию. Динамические нагрузки подразделяются на внезапно приложенные, повторно-переменные и ударные. Примером внезапно приложенной нагрузки может служить действие веса железнодорожного состава, проходящего через мост; повторно-переменной – нагрузка на шатун в двигателе внутреннего сгорания; ударной – действие силы удара молота на его фундамент или гидравлический удар в гидросистеме. Ударные нагрузки возникают также в случае плохой пригонки или износа сопряженных деталей, когда зазоры превышают величину, допустимую по конструктивным и технологическим условиям. Например, при износе зубьев шестерен или деталей шариковых подшипников в машине возникают характерные стуки, свидетельствующие о возникновении ударных нагрузок, быстро приводящих к выходу конструкции из строя.

Динамические нагрузки также подразделяются на периодические и случайные нагрузки. К случайным нагрузкам относятся нагрузки, действующие на детали автомобилей, тракторов, станков, а также нагрузки, действующие на сооружения (дома, мачты, краны и т.п.) от давления ветра, снега и т.п.

Более глубокое изучение таких нагрузок возможно лишь с помощью методов статистики и теории вероятности, которые применяются при изучении случайных величин.

Временная нагрузка может сохранять более или менее постоянную величину в течение всего периода ее действия, а может непрерывно изменяться по некоторому закону; в последнем случае она называется переменной нагрузкой.

Если переменная нагрузка изменяется по циклическому (повторяющемуся) закону, то она называется циклической.

В машиностроении расчетные нагрузки определяются в зависимости от конкретных условий работы машины: по номинальным значениям мощности, угловой скорости отдельных ее деталей, силы тяжести, сил инерции и т. п. Например, при расчете деталей трехтонного автомобиля учитывают номинальный полезный груз, равный 3 тонны. Возможность же перегрузки автомобиля учитывают тем, что размеры сечения деталей назначают с некоторым запасом прочности.

Скорость роста усилий при динамическом нагружении не обеспечивает равновесности процессов, протекающих в материале, в результате чего возникают многочисленные нарушения внутренней структуры материала. При систематическом чередовании нагружения и разгрузки накопление дефектов структуры ведет к возникновению микроскопических трещин, слияние которых приводит к усталостному разрушению.

По отношению к выбранному материальному телу (элементу конструкции) все действующие силы подразделяются на внешние и внутренние силы. Под внешними силами (нагрузками) понимаются силы взаимодействия данного материального тела со всеми другими окружающими его телами.

Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой. Вообще внутренние силы возникают между всеми смежными частицами тела при нагружении.

Понятно, что деление сил (нагрузок) на внешние и внутренние силы является условным. Одна и та же сила может быть и внутренней и внешней, всё зависит от выбора объекта исследования. В сопротивлении материалов считается, что если нет внешних сил, то отсутствуют и внутренние, то есть, справедлива гипотеза о ненапряженном начальном состоянии тела.

Для выявления внутренних сил и последующего их определения применяют метод сечений, суть которого заключается в следующем. Пусть к элементу сооружения, имеющего форму бруса, приложена система внешних сил, удовлетворяющая условиям равновесия. Под действием этой нагрузки в элементе возникают внутренние силы. В произвольном месте мысленно рассечем брус поперечным сечением на две части (рис. 8, а).

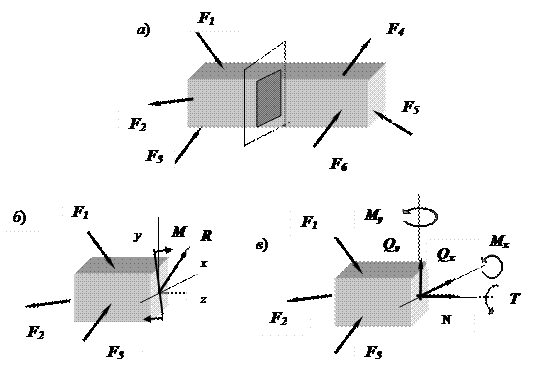
Рис.8. Определение внутренних сил методом сечений: а) – элемент до рассечения поперечным сечением;

б) – приведение системы внутренних сил к центру тяжести сечения; в) – разложение главного вектора и главного момента по осям координат

Так как связи между частями устранены, то необходимо действие правой части на левую, и левой на правую заменить системой сил в этом сечении. Эти силы определяют взаимодействие между частицами тела, расположенными по разные стороны от мысленно проведенного сечения, и поэтому являются внутренними для тела в целом. Согласно закону действия и противодействия система сил, возникающих на поверхности сечения в левой отсеченной части, равна, но обратна по знаку системе сил на поверхности сечения в правой отсеченной части. Согласно допущению о сплошности материала следует считать, что внутренние силы распределены по сечению непрерывно по некоторому не известному нам закону.

Внутренние усилия должны быть так распределены по сечению, чтобы деформированные поверхности сечения при совмещении правой и левой частей тела в точности совпадали. Это требование в механике твердого деформируемого тела носит название условия неразрывности деформаций.

Рассмотрим отдельно какую-либо из отсеченных частей бруса, например левую. Внутренние силы, возникающие в сечении целого бруса по отношению к рассматриваемой отсеченной части бруса, являются внешними и дополняют систему заданных внешних сил до равновесной. Приведем систему внутренних сил к центру тяжести сечения (рис. 8, б). В результате получим главный вектор R и главный момент M.

Выберем систему координат так, чтобы ось z совпала с нормалью к сечению (располагалась вдоль оси элемента), а оси у и x лежали в плоскости нормального сечения. Разложив главный вектор и главный момент по осям координат, получим составляющие: три силы и три момента. Эти составляющие называют внутренними силовыми факторами в сечении бруса, каждая из которых имеет свое наименование: N - нормальная сила; Q_y и Q_z - поперечные силы; Т - крутящий момент; M_z и М_у - изгибающие моменты относительно осей x и y (рис. 8, в).

При известной нагрузке все шесть внутренних силовых факторов могут быть определены из уравнений равновесия составленных для рассматриваемой части бруса. Заметим, что в каждое уравнение войдут проекции на соответствующую ось (или моменты относительно оси) всех внешних сил, приложенных к рассматриваемой части, и только один из внутренних силовых факторов.

ΣZ = ΣF_z^отс + N = 0; Σm_z = ΣM_z^отс + T = 0;

ΣY = ΣF_y^отс + Q_y = 0; Σm_y = ΣM_y^отс + M_y = 0;

ΣX = ΣF_x^отс + Q_x = 0; Σm_x = ΣM_x^отс + M_x = 0.

Уравнения равновесия позволяют сформулировать правило определения каждого из внутренних силовых факторов:

Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на ось z, всех внешних сил, действующих на одну из отсеченных (левую или правую) частей бруса.

N = ΣF_z^отс.

То же для определения поперечных сил Q_y и Q_x,, только проектировать внешние силы необходимо на оси y и x.

Q_y = ΣF_y^отс,

Q_x = ΣF_x^отс.

Изгибающие моменты M_x и M_y и крутящий момент T, численно равны алгебраической сумме моментов всех сил по одну сторону от сечения, относительно соответствующих осей x, y и z.

T = ΣM_z^отс,

M_x = ΣM_x^отс,

M_y = ΣM_y^отс.

Для установления знака внутреннего силового фактора будем придерживаться следующих правил:

Условимся продольную силу считать положительной, если она вызывает растяжение, т.е. направлена от сечения и отрицательной, если она вызывает сжатие, т. е. направлена к сечению.

При решении задач знак N удобнее устанавливать в зависимости от направления внешних сил. Если внешняя сила, направлена в противоположную от сечения сторону, то она вызывает в нем положительную продольную силу (растяжение), и наоборот, если внешняя сила, направлена к сечению, то она вызывает в нем отрицательную продольную силу (сжатие) (рис. 9, а).

Поперечную силу Q будем считать положительной, если она направлена так, что стремиться повернуть отсеченную часть бруса по ходу часовой стрелки (рис. 9, б), и отрицательной, если - против хода часовой стрелки.

Согласно этому правилу внешняя сила, стремящаяся повернуть рассматриваемую часть бруса относительно сечения по ходу часовой стрелки, вызывает в сечении положительную поперечную силу

Крутящий момент Т будем считать положительным, если при взгляде со стороны внешней нормали на рассматриваемое сечение он направлен по ходу часовой стрелки или внешний скручивающий момент направлен против хода часовой стрелки (рис.9, в).

Изгибающий момент Mx считается положительным, если он вызывает растяжение нижних волокон рассматриваемой части бруса. В противном случае изгибающий момент считается отрицательным (рис. 9, г).

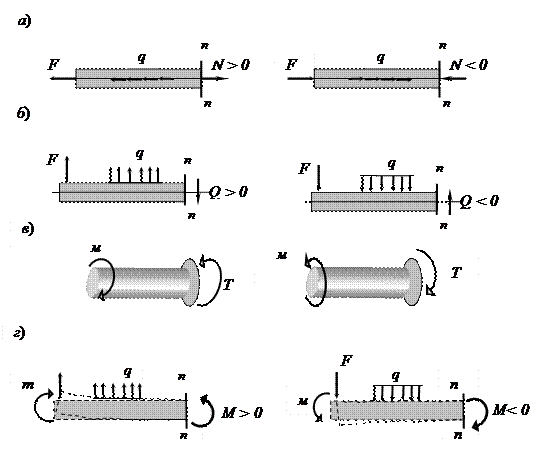
Рис. 9. Виды сопротивлений:

а) растяжение (сжатие); б) сдвиг; в) кручение; г) изгиб

Согласно принятому правилу знаков для изгибающего момента, если внешняя сила, приложенная к рассматриваемой части бруса изгибает участок, расположенный между сечением точкой ее приложения выпуклостью вниз, то изгибающий момент положительный. Отрицательному значению изгибающего момента соответствует противоположное направление выпуклости балки

Таким образом, метод сечений позволяет найти значения внутренних силовых факторов и установить вид нагружения в любом сечении бруса при действии любой нагрузки. Для этого необходимо выполнить следующее:

1. Мысленно рассекаем брус на две части в пределах исследуемого i–го участка.

2. Оставляем ту часть бруса, на которую действует меньше сил.

3. Заменяем действие условно отброшенной части бруса положительными внутренними силовыми факторами, приведенными к центру тяжести исследуемого сечения бруса.

4. Выберем для оставленной части бруса скользящую систему координат (начало координат совмещаем с границей участка, положение исследуемого сечения определяется координатой z_i, где 0≤z_i≤c и c – длина i-го участка).

5. Определяем искомые внутренние силовые факторы из уравнений равновесия ΣZ = 0; ΣY = 0; ΣX = 0; Σm_z = 0; Σm_y = 0; Σm_x = 0, которые составляем для оставленной части бруса.

Проверка правильности определения усилий ведется в двух направлениях: а) выполнение условий равновесия, не использованных при определении внутренних усилий; б) проверка равновесия части тела, которая не рассматривалась при решении задачи.

В зависимости от вида внутренних силовых факторов, возникающих в сечении, различают различные следующие виды нагружения бруса.

- Растяжение или сжатие. Действует только продольная сила N.

- Кручение. Действует только крутящий момент T.

- Сдвиг. Действует только поперечная сила Q_x или Q_y

- Изгиб. Действует только изгибающий момент M_x или M_y (чистый изгиб), при действии изгибающего момента и поперечной силы (поперечный изгиб).

- Сложное сопротивление. Одновременное действие нескольких силовых факторов. Например, M_x и T, M и N.

Итак, внутренние усилия в сечении есть функции параметров, определяющих положение сечения в теле, и нагрузок по одну сторону от сечения. Эти функции могут быть представлены аналитически или графически. График, показывающий изменение внутреннего усилия в зависимости от положения сечения, называется эпюрой. Ординаты усилий в определенном масштабе откладывают от линии, соответствующей оси бруса.

Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими n, q_y, q_z, и интенсивностью моментов с составляющими t, m_y, m_z. Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.10) составим дифференциальные уравнения равновесия.

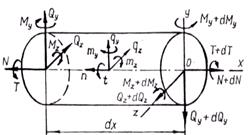
Рис. 10

Из условий ΣX=0, ΣY=0, ΣZ=0, ΣM_x=0, следуют уравнения:

Из условий ΣM_y=0, ΣM_z=0 получаем:

откуда, пренебрегая бесконечно малыми второго порядка, находим

Подставляя выражения Q_y и Q_z в соответствующие дифференциальные уравнения, получаем

Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:

Постоянные интегрирования С_i (i=1,2,...,6) определяются из граничных условий для рассматриваемых внутренних усилий.

Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.

Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре M_z(M_y) определить характер эпюры Q_y(Q_z). В частности, на участках, где m_z=0 (m_y=0), т.е. при соблюдении зависимостей

можно установить, что при М_z = const имеем Q_y = 0 (при М_y = const имеем Q_z = 0). Переменная величина M_z(M_y) достигает экстремальных значений в точках, где Q_y = 0 (Q_z = 0).

При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью.

Допущения, применяемые в сопротивлении материалов

Для построения теории сопротивления материалов принимают некоторые понятия и допущения относительно структуры и свойств материалов, а также о характере деформаций. Приведем основные из них.

1. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры. Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее, указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых существенно превышают не только межатомные расстояния, но и размеры кристаллических зерен.

С понятием однородности тесно связано понятие сплошности среды, под которым подразумевают тот факт, что материал конструкции полностью заполняет весь отведенный ему объем, а значит в теле конструкции нет пустот и не учитывается реальная структура материала (зернистая, кристаллическая и др.). Это допущение позволяет использовать в сопротивлении материалов методы математического анализа (дифференциальное и интегральное исчисления). Для большинства машиностроительных конструкций расчеты, основанные на допущении о сплошности строения дают практически удовлетворительные результаты. Это объясняется тем, что размеры детали во много раз больше межатомных расстояний.

2. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево, ткани (косой и кривой крой), армированная пластмасса, бетон). К анизотропным относятся и материалы с направленной кристаллизацией и с монокристаллической структурой. Отдельно взятый кристалл материала анизотропен, но т.к. в объеме реального тела содержится бесконечно большое количество хаотично расположенных кристаллов, принимается, что материал изотропен.

Металлы и сплавы, как правило, изотропны, так как большинство металлов имеет мелкозернистую структуру. Благодаря большому количеству кристаллов свойства материалов выравниваются в различных направлениях и можно считать эти материалы практически изотропными. В настоящее время широкое распространение получили анизотропные композиционные материалы, состоящие из двух компонентов – наполнителя и связующего. Наполнитель состоит из уложенных в определенном порядке высокопрочных нитей – матрицы, что и определяет значительную анизотропию композита. Композиционные материалы имеют высокую прочность при значительно меньшем, чем металлы весе.

3. Принимается, что до определенной величины деформации материалов подчиняются закону Гука и весьма малы относительно размеров тела, поэтому все расчеты выполняются по исходной, т.е. недеформированной, схеме, к которой применим принцип независимости действия сил (принцип суперпозиции).

Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке (рис. 11). Под словами «результат воздействия» следует понимать – деформации, внутренние силы и перемещения отдельных точек.

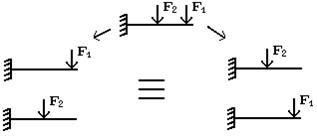
Рис. 11. Использование принципа суперпозиции

Должны соблюдаться два условия:

1. перемещения малы по сравнению с размерами тела,

2. перемещения линейно зависят от силы.

С помощью этого принципа сложный случай приводится к простым.

4. После снятия нагрузки геометрические размеры тела полностью или частично восстанавливаются. Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью. При решении большинства задач в сопротивлении материалов принимается, что материал конструкций абсолютно упругий. Это допущение справедливо, пока нагрузки не превышают определенного значения. При больших нагрузках в элементах конструкций появляются пластические деформации. Пластичностью называется свойство тела сохранять после прекращения действия нагрузки, или частично полученную при нагружении, деформацию.

Ползучестью называется свойство тела увеличивать деформацию при постоянных внешних нагрузках.

5. Перемещения, возникающие под действием внешних сил в упругом теле, малы по сравнению с его размерами. Это допущение называется принципом начальных размеров. В большинстве случаев механические конструкции работают в упругой зоне (в зоне действия закона Гука), а упругие деформации малы по сравнению с геометрическими размерами (рис. 12). Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции.

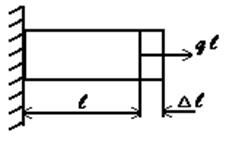
∆l≪l

Рис.12. Принцип неизменности геометрических размеров

6. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения. Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напряженного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня или другое определение: в точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил весьма мало зависит от конкретного способа приложения этих нагрузок, а зависит только от ее статического эквивалента (рис. 13). Этот принцип во многих случаях позволяет производить замену одной системы сил другой системой, статически эквивалентной, что позволяет часто значительно упростить расчет. Принцип Сен-Венана подробно рассмотрен в части 2.

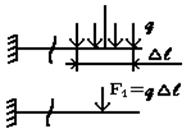
Рис.13. Использование принципа Сен-Венана

7. Принимается гипотеза плоских сечений (гипотеза Бернулли), введенной швейцарским ученым Д. Бернулли, гласящей, что плоские поперечные сечения стержня до деформации остаются плоскими и после деформации (рис.14).

Рис.14. Гипотеза плоских сечений

8. Считается, что ненагруженное тело свободно от каких бы то ни было внутренних сил любой природы. Изменению формы и размеров тела под нагрузкой сопротивляются силы взаимодействия между частицами материала, называемые силами упругости. В дальнейшем, говоря о внутренних силах, будем иметь в виду именно эти силы упругости, не принимая во внимание молекулярные силы, имеющиеся и в ненагруженном теле. Это допущение полностью не выполняется ни для одного материала. Причины возникновения неравномерных внутренних или начальных усилий:

- В стальных деталях из-за неравномерного остывания;

- В дереве из-за неравномерного высыхания;

- В бетоне в процессе твердения.

В тех случаях, когда есть основания предполагать, что эти силы значительны, стараются определить их экспериментально. Однако, часто они достаточно малы, чтобы их учитывать.

Использование этих понятий и допущений существенно упрощает изучение поведения конструкций под нагрузкой, а соответствие условного материала реальным материалам достигается введением в расчет элементов сооружений экспериментально получаемых механических характеристик реальных материалов.

Напряжения

При определении внутренних силовых факторов их считают приложенными в центре тяжести сечения. В действительности внутренние силы, являясь результатом взаимодействия частиц тела, непрерывно распределены по сечению. Интенсивность этих сил в разных точках сечения может быть различной. При увеличении нагрузки на элемент конструкции увеличиваются внутренние силы и соответственно увеличивается их интенсивность во всех точках сечения. Если в некоторой точке интенсивность внутренних сил достигнет определенного для данного материала значения, в этой точке возникает трещина, развитие которой приведет к разрушению элемента, или возникнут недопустимые пластические деформации. Следовательно, о прочности элементов конструкций следует судить не по значению внутренних силовых факторов, а по их интенсивности. Меру интенсивности внутренних сил называют напряжением.

В окрестности произвольной точки, принадлежащей сечению некоторого нагруженного тела, выделим элементарную площадку , в пределах которой действует внутреннее усилие ∆F (рис. 15, а).

Среднее значение интенсивности внутренних усилий на площадке, называемое средним напряжением, определяют по формуле

Уменьшая площадь ∆A, в пределе получаем истинное напряжение в данной точке сечения

Векторная величина p называется полным напряжением в точке. В международной системе единиц (СИ) за единицу напряжения принят паскаль (Па=Н/м²) – это напряжение, при котором на площадке 1 м² действует внутренняя сила 1 Н.

Так как эта единица очень мала, в расчетах используют кратную единицу напряжения – мегапаскаль (1 МПа=10⁶ Па).

Разложим вектор полного напряжения p на две составляющие (рис.15, б).

Проекция вектора полного напряжения p на нормаль к данной площадке обозначается через σ и называется нормальным напряжением.

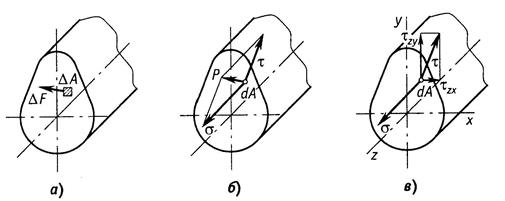
Рис. 15

Составляющую, лежащую в сечении в данной площадке обозначается через τ и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие и (рис.15, в). Первый индекс при τ показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов.

Между полным напряжением и его составляющими существует зависимость

Через точку тела можно провести бесконечное число сечений и для каждого из них напряжения имеют свое значение. Следовательно, при определении напряжений необходимо указывать положение не только точки тела, но и сечения, проведенного через эту точку.

Совокупность напряжений для множества элементарных площадок, проходящих через данную точку, образует напряженное состояние в этой точке.

В дифференциальные уравнения равновесия бесконечно малого прямоугольного параллелепипеда входят шесть независимых скалярных величин, соответствующих составляющим напряжений по его граням. Они определяют тензор напряжений:

При этом учитывается свойство парности касательных напряжений (τ_xy = τ_yx, τ_xz = τ_zx, τ_yz= τ_zy): на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к линии пересечения площадок, равны по величине и взаимно направлены либо к линии пересечения, либо от нее.

Если площадка dA совпадает с поверхностью тела, то составляющие напряжения трансформируются в составляющие внешних сил, действующих на поверхности тела. Соответствующие уравнения выражают условия на поверхности, или статические граничные условия.

Площадка, на которой касательные напряжения равны нулю, называется главной. Через точку проходят три главные площадки. По ним действуют главные напряжения, которые обозначаются σ₁, σ₂, σ₃ (σ_1≥σ₂ ≥σ₃).

Напряжения в поперечных сечениях связаны с внутренними силовыми факторами определенными зависимостями.

Возьмем в сечении бесконечно малую площадку площадью dA. По этой площадке в общем случае действуют бесконечно малые (элементарные) внутренние силы (рис. 16)

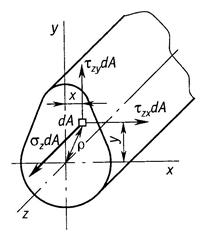
Рис.16

Соответствующие элементарные моменты относительно координатных осей x, y, z имеют вид:

Просуммировав бесконечно малые силы и моменты, действующие в сечении, получим выражения, связывающие внутренние силовые факторы с напряжениями:

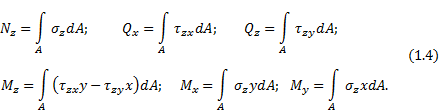
В соответствии с теоремой Вариньона, известной из теоретической механики, и зависимостью между напряжениями τ, и , выражение для можно записать в виде

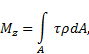
где

Интегральные зависимости (1.4) можно использовать для определения напряжений по найденным методом сечений внутренним силовым факторам при условии, что известны законы распределения напряжений по сечению. Поскольку эти законы зависят от вида деформации, то обратная задача (определение напряжений через внутренние усилия) решается путем совместного использования условий равновесия и условий деформирования тела. Задача становится статически неопределимой.

Перемещения и деформации

Под действием внешних сил твердые тела изменяют свою геометрическую форму, то есть деформируются. Если в теоретической механике тела считаются абсолютно жесткими, то в сопротивлении материалов тела обладают способностью деформироваться, т.е. под действием внешней нагрузки изменять свои начальные размеры и форму. Точки тела при этом неодинаково перемещаются в пространстве. Вектор , имеющий свое начало в точке А недеформированного состояния, а конец в т. деформированного состояния, называется вектором полного перемещения т. А (рис. 17, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформированного состояния, расположенные на расстоянии S друг от друга (рис. 17, б).

Рис. 17

Пусть в результате изменения формы тела эти точки переместились в положение и , соответственно, а расстояние между ними увеличилось на величину DS и составило S + DS. Величина

называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы , , .

Линейные деформации , , характеризуют изменения объема тела в процессе деформирования, а формоизменения тела - угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрезками ОD и ОС (рис. 17, б). При действии внешних сил указанный угол DOC изменится и примет новое значение . Величина

называется угловой деформацией, или сдвигом в точке О в плоскости СОD. Относительно координатных осей деформации сдвига обозначаются , , .

Линейные и угловые деформации – величины безразмерные. Деформацию , , часто называют относительной линейной деформацией, а , , – относительным сдвигом.

Положительными принимают линейную деформацию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первоначального угла пересечения отрезков. Полагая деформации малыми, мы можем в дальнейшем пренебрегать ими по сравнению с единицей, а также их высокими степенями по сравнению с первой степенью.

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформированное состояние в точке. В случае малых деформаций оно полностью определяется линейными деформациями трех взаимно перпендикулярных линейных элементов тела, проходящих через данную точку, и тремя деформациями сдвига этих линейных элементов. Соответствующие шесть независимых скалярных величин определяют тензор деформаций:

Главные оси деформации – три взаимно перпендикулярные прямые, проходящие через данную точку тела и совпадающие по направлениям с такими тремя линейными элементами тела, которые остаются взаимно перпендикулярными и после деформации. Линейные деформации по направлениям этих осей называются главными деформациями и обозначаются ε₁, ε₂, ε₃ (ε₁≥ε₂≥ε₃).

Следует подчеркнуть, что в сопротивлении материалов слово деформация имеет данное выше строгое определение и выступает как количественная мера изменения геометрических размеров в окрестностях точки.

Закон Гука и принцип независимости действия сил

Многочисленные экспериментальные наблюдения за поведением деформируемых тел показывают, что в определенных диапазонах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Р.Гуком в формулировке «ut tensio sic vis» - «какого растяжение - такова и сила» и носит название закона Гука.

В соответствии с этим законом перемещение произвольно взятой точки А (рис. 17, а) нагруженного тела по некоторому направлению, например, по оси x, а может быть выражено следующим образом:

где Р - сила, под действием которой происходит перемещение u; - коэффициент пропорциональности между силой и перемещением.

Очевидно, что коэффициент зависит от физико-механических свойств материала, взаимного расположения точки А и точки приложения и направления силы Р, а также от геометрических особенностей системы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.

В современной трактовке закон Гука определяет линейную зависимость между напряжениями и деформациями, а не между силой и перемещением.

Касательные напряжения τ вызывают угловые деформации γ, причем при малых деформациях они не влияют на изменение линейных размеров и, следовательно, на линейные деформации. Нормальное напряжение σ не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними.

Параметры E и G, входящие в эти формулы, называют модулями упругости материала соответственно первого и второго рода. Они характеризуют его сопротивляемость деформированию, или жесткость в упругой стадии деформации. При одном и том же напряжении деформации больше у того материала, у которого меньше модуль упругости. Численные значения E и G для каждого конструктивного материала определяются экспериментально. Они имеют размерности напряжений. На практике удобно использовать единицы, кратные паскалю: мегапаскаль (1 МПа=10⁶ Па) и гигапаскаль (1 ГПа=10⁹ Па).

При растяжении или сжатии одновременно с продольной деформацией ε =∆l/l (рис. 18, а), в элементе возникает поперечная деформация = -∆а/а.

Отношение

называют коэффициентом Пуассона.

Величины коэффициента Пуассона и модуля упругости для различных материалов определяют опытным путем и их значения приведены в ГОСТ. Между модулем упругости и модулем сдвига существует зависимость

Установим связь между нормальными напряжениями и линейными деформациями, справедливые для любого напряженного состояния. Рассмотрим бесконечно малый элемент, имеющий форму кубика, на гранях которого возникают напряжения растяжения σ_x, σ_y, σ_z. При действии только напряжения σ_x, элемент получает продольную деформацию в направлении оси х, равную, согласно закону Гука, σ_x/Е (рис. 18,б). Одновременно его размеры вдоль осей y и z уменьшатся, при этом соответствующие поперечные деформации будут равны

Аналогичное действие оказывает растягивающие напряжения σ_y и σ_z.. Каждое из них вызывает продольную деформацию в своем направлении σ_у/Е и σ_z/Е и поперечные деформации по двум другим направлениям (рис. 18,в, г).

Суммируя деформации в направлениях каждой оси, получаем

Эти зависимости представляют собой математические выражения обобщенного закона Гука. Напряжения σ_x, σ_y, σ_z следует подставлять в формулы со своим знаком.

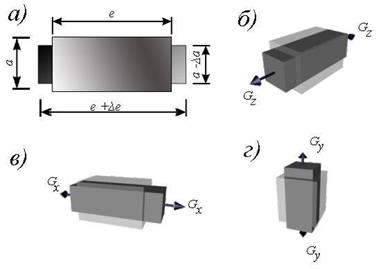
Рис. 18. Деформация элемента при растяжении:

а) общий вид элемента; б) деформации в направлении оси z;

в) то же оси x; г) то же оси у

Системы, для которых соблюдается условие пропорциональности между напряжениями и деформациями, подчиняются принципу суперпозиции, или принципу независимости действия сил.

В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.

Общие принципы расчета конструкции

В результате расчета нужно получить ответ на вопрос, удовлетворяет или нет конструкция тем требованиям прочности и жесткости, которые к ней предъявляются. Для этого необходимо прежде всего сформулировать те принципы, которые должны быть положены в основу оценки условий достаточной прочности и жесткости.

Условие невозникновения предельного состояния (условие прочности) в материале в рассматриваемой точке тела имеет форму неравенства

σ_пред (или σ_red)< σ_max ,

которое отражает сущность так называемого поверочного расчета.

Методы расчета конструкций выбираются в зависимости от условий работы конструкций и требований, которые к ней предъявляются. Так, наиболее распространенным методом расчета деталей машин на прочность является расчет по методу допускаемых напряжений. В основу этого метода положено предположение, что определяющим параметром надежности конструкции является напряжение или, точнее говоря, напряженное состояние в точке. Если предельным состоянием материала в локальной области является хрупкое разрушение, то это может представить опасность для всей конструкции в силу развития области разрушения. В этой ситуации использование метода допускаемых напряжений является вполне обоснованным.

Расчет выполняется в следующем порядке.

На основании анализа напряженного состояния конструкции выявляется та точка сооружения, где возникают наибольшие расчетные (рабочие) напряжения . Расчетная величина напряжений сопоставляется с предельно допустимой величиной напряжений (или σ_red) для данного материала, полученной на основе предварительных лабораторных испытаний. Чтобы не нарушилась прочность элемента, рабочие напряжения в любой его точке должны быть меньше предельных. Для особо ответственных конструкций, для которых требуется не допускать возникновения пластических деформаций, за величину (или σ_red) принимается . В тех случаях, когда допустимо возникновение пластических деформаций, как правило, принимается . Для хрупких материалов, а в некоторых случаях и умеренно пластических материалов, принимается .

Для надежной работы элемента нельзя допустить, чтобы рабочие (расчетные) напряжения в наиболее напряженной точке были близки к предельным, нужно обеспечить запас прочности.

Отношение предельного напряжения для материала, из которого изготовлен элемент конструкции, к максимальному рабочему напряжению называют коэффициентом запаса прочности (или коэффициентом безопасной прочности).

Выбор коэффициента запаса прочности – один из основных и наиболее ответственных этапов расчета на прочность. При заниженном коэффициенте запаса прочности снижается надежность работы детали, повышается опасность ее разрушения при эксплуатации. При завышении запаса прочности увеличивается масса и стоимость детали.

Коэффициент запаса учитывает следующие основные факторы.

1. Погрешности в создании рабочей модели. Т.е. способы определения усилий в элементах конструкций сопряжены с некоторыми условностями.

2. Заданные нагрузки не вполне достоверны. Возможны превышения нагрузки в процессе эксплуатации.

3. Степень ответственности изделия.

4. Размеры сечений имеют некоторые допуски при изготовлении и могут меняться в течение срока службы конструкции (износ, коррозия и т.д.).

5. Несовершенства в определении свойств материала. Величины, характеризующие прочность и пластичность материала, могут быть разными для разных партий материала одной и той же категории.

6. Величины, характеризующие прочность и пластичность материала, могут быть разными для разных партий материала одной и той же категории; д) в некоторых случаях учет концентрации напряжений связан с рядом грубых допущений.

7. Необходимо считаться с особенностями действия динамических нагрузок и некоторыми другими факторами.

8. Вероятность возможных экстремальных ситуаций (землетрясение, случайный удар и т.п.).

При назначении коэффициента запаса прочности учитывают, насколько точно можно для проектируемой детали определить рабочее и предельное напряжения. Рабочие напряжения нельзя определить абсолютно точно, так как фактические, действующие на элемент конструкции нагрузки могут существенно отличаться от используемых в расчете. В процессе эксплуатации конструкции возможно кратковременное увеличение нагрузок (перегрузки), часто нагрузки непрерывно изменяются или носят случайный характер (например, нагрузки на крыло летящего самолета). Формулы сопротивления материалов основаны на определенных допущениях, упрощающих расчеты, и, следовательно, не обеспечивают высокой точности. В деталях сложной формы напряжения, как правило, можно определить только приближенно. Предельные напряжения, характеризующие прочность материала, также нельзя определить абсолютно точно вследствие непостоянства химического состава сплавов в различных плавках, отклонений в режимах технологического процесса изготовления материалов, погрешностей при испытании образцов. При расчете элемента конструкции необходимо учитывать возможные последствия его разрушения.

Так как все факторы, влияющие на прочность элемента конструкции, учесть точно в расчете невозможно, в расчет вводят требуемый (допускаемый) коэффициент запаса прочности , гарантирующий надежную работу элемента конструкции в течение требуемого срока службы (табл.1)

Таблица 1. Ориентировочные значения допускаемого коэффициента

запаса прочности

Вид материала	Характер нагрузки	Коэффициент запаса прочности
Пластичный	Статическая	2,4-2,6
	Ударная	2,8-5,0
	Повторно-переменная	5,0-15,0
Хрупкий	Статическая	3,0-9,0

Часто этот коэффициент представляют в виде произведения частных коэффициентов запаса каждый из которых учитывает влияние на прочность элемента конструкции какого-либо одного ил нескольких факторов.

В каждой отрасли машиностроения существуют нормы на допускаемые запасы прочности, основанные на большом опыте расчета деталей и их эксплуатации. Определяемые по нормам коэффициенты запасы прочности называют нормативными.

Прочность элемента конструкции считают обеспеченной, если расчетный коэффициент запаса не меньше допускаемого

Это равенство называют условием прочности.

Если установлен допускаемый коэффициент запаса прочности и для выбранного материала известно предельное напряжение, определяют максимальное напряжение, которое можно допустить для надежной работы элемента конструкции. Такое напряжение называют допускаемым

Часто величина допускаемого напряжения берется из таблиц, составленных на основе действующих норм (см. «Справочные данные»).

В практических расчетах считают, что прочность элемента конструкции обеспечена, если возникающие в нем максимальные напряжения не превышают допускаемых. Условие прочности имеет вид

Если материал имеет различные предельные напряжения при растяжении и сжатии, то допускаемое напряжение обозначают соответственно и .

Чтобы уточнить, какое напряжение принято в качестве предельного (предел текучести или прочности ), иногда в обозначения расчетных и допускаемых коэффициентов запаса прочности вводят соответствующие индексы: ; ; ; .

Указанный метод является не единственным. Если предельным состоянием материала в локальной области является наступление текучести, то разрастание охваченной ею области возможно лишь при снятии стеснения со стороны материала, находящегося в упругом состоянии. Именно поэтому расчет по допускаемым напряжениям в случае пластического состояния материала не является совершенным, поскольку предельное состояние материала в окрестности точки не представляет опасности для всей конструкции.

В этом случае более совершенным является метод разрушающих нагрузок.

В этом методе путем расчета определяется предельная нагрузка, которую может выдержать конструкция, не разрушаясь и не изменяя существенно свою форму. Предельная (разрушающая) нагрузка сопоставляется с проектной нагрузкой, и на этом основании делается вывод о несущей способности конструкции в эксплуатационных условиях.

Условие прочности можно представить в виде

где n- коэффициент запаса прочности, принимаемый таким же, как и в методе допускаемых напряжений.

При определении разрушающей нагрузки для конструкций из пластичного материала применяется схематизированная диаграмма напряжений - диаграмма Прандтля (рис.19). Схематизация диаграммы заключается в предположении, что материал на начальном этапе деформирования находится в упругой стадии вплоть до предела текучести, а затем материал обладает неограниченной площадкой текучести. Материал, работающий по такой диаграмме, называется идеально упруго-пластическим. Такая схематизированная диаграмма деформирования в большей степени соответствует действительной диаграмме деформирования материала, имеющего ярко выраженную площадку текучести, т.е. пластичным материалам.

Следует заметить, что определение разрушающей нагрузки возможно только для несложных расчетных схем.

Рис.19

Расчет по разрушающим нагрузкам был внедрен в нашей стране в 1938 г. применительно к строительным конструкциям. Это приблизило результаты расчета к фактической несущей способности конструкций, но не дало исчерпывающего представления о степени их надежности.

Естественным завершением инженерного поиска в этом направлении был переход к методу расчета по предельным состояниям, который был осуществлен в нашей стране в 1955 г. по предложению Н.С.Стрелецкого. Этот метод положен в основу отечественных норм проектирования строительных конструкций.

Согласно ему предельным считается состояние, при котором конструкция перестает удовлетворять эксплуатационным требованиям или требованиям, предъявляемым в процессе возведения здания или сооружения. Современные отечественные нормы проектирования отмечают две группы предельных состояний. Первая группа квалифицирует непригодность конструкции к эксплуатации по причине потери несущей способности, вторая − непригодность к эксплуатации в связи с нарушениями требований строительных норм и правил (СниП), таким, как чрезмерные деформации, образование и чрезмерное раскрытие трещин. В правильно запроектированном сооружении не должно возникнуть ни одно из этих предельных состояний, т. е. должна быть обеспечена надежность сооружения.

Надежностью называется способность сооружения сохранять в процессе эксплуатации качества, заложенные при проектировании. Надежность зависит от точно учета многих факторов среди них: нагрузки или другие воздействия, механические свойства материалов, геометрические параметры конструктивных элементов, условия работы сооружения, степень ответственности сооружения и др. Значения перечисленных факторов, при которых обеспечена нормальная эксплуатация сооружения, называются нормативными характеристиками и определяются по СниПу.

Расчет по первой группе предельных состояний обеспечивает надежность конструкции в отношении хрупкого, вязкого и иного вида разрушения, потери устойчивого равновесия.

Расчет по второй группе предельных состояний производится по двум условиям:

1) перемещения элемента конструкции под нагрузкой не должны превышать предельного значения, определяемого нормами;

2) трещиностойкость конструкции должна быть обеспечена на соответствующем уровне в зависимости от условий, в которых она работает; речь идет о недопущении образования трещин или допускаемых ограничениях по ширине их непродолжительного и продолжительного раскрытия.

Поверочный расчет конструкции по предельным состояниям основывается на условии

φ ≤ φ_cal , (1.18)

где φ_cal – расчетный фактор, отклоняющийся от предельного значения φ_b.

Важным преимуществом нового метода является отказ от детерминистического подхода к нагрузкам и механическим свойствам материалов, выявление их вероятностной природы.

Наиболее часто повторяющаяся нагрузка называется нормативной (N_n). Она устанавливается нормами с учетом вероятности превышения ее среднего значения. Наибольшая нагрузка, которая может проявиться за время существования конструкции, называется расчетной (N) и вычисляется по формуле

N = N_n γ_f , (1.19)

где γ_f – коэффициент надежности по нагрузке.

В случае нагрузки от собственной массы γ_f = 1,05...1,3 (в зависимости от вида материала конструкции и условий его изготовления); в случае снеговой нагрузки γ_f = 1,4...1,6. В ряде случаев коэффициент γ_f может быть меньше 1, если это ухудшает условия работы конструкций. Например, в целях предотвращения потери равновесия тела, вызываемой опрокидыванием или скольжением, принимают для собственной массы γ_f = 0,9. Коэффициент надежности по нагрузке при расчете по второй группе предельных состояний принимается, как правило, равным единице.

Нормативное сопротивление R_n материала силовым воздействиям определяется экспериментально путем выборочных испытаний образцов стандартных размеров и отражает по существу браковочный минимум прочностных свойств материала. Вероятность, с которой обеспечивается нормативное сопротивление, должна составлять не менее 95%. В зависимости от механических свойств величина R_n принимается по пределу текучести или по временному сопротивлению.

Наименьшая возможная величина сопротивления материала называется расчетным сопротивлением R, причем

где γ_m – коэффициент надежности по материалу.

Коэффициент γ_m учитывает изменчивость механических свойств материала и минусовые допуски при производстве элементов конструкций. Он лежит в пределах 1,025...1,3.

Назовем остальные коэффициенты метода расчета по предельным состояниям. Коэффициент условий работы γ_c учитывает влияние конкретных условий работы конструкции, например, приближенный характер расчетных схем, условность предпосылок расчета, агрессивность среды и другие факторы.

Коэффициент надежности по назначению γ_n учитывает степень ответственности конструкции и значимость последствий наступления тех или иных предельных состояний.

Как правило, на конструкцию действует несколько нагрузок. Вместе с тем их одновременное действие при наибольших величинах маловероятно. Например, трудно предположить одновременно ураганный ветер, наибольшую снеговую нагрузку и максимальную полезную нагрузку на конструкции здания. С целью приближения вводимых нагрузок к реальности используется коэффициент сочетаний n_c <1.

Надежность и гарантия от возникновения предельных состояний первой группы (по несущей способности) обеспечивается при выполнении следующего условия:

σ_max ≤ R (1.21)

Здесь σ_max – максимальное расчетное напряжение, возникающее в элементе конструкции при самых неблагоприятных нагрузках и воздействиях.

Следовательно, физический смысл формулы (1.21) заключается в том, чтобы максимальное расчетное напряжение в элементе не превышало расчетного сопротивления материала.

Гарантией предотвращения наступления предельного состояния второй группы – по непригодности к нормальной эксплуатации вследствие недопустимых перемещений (прогибов, осадок, углов поворота) является следующее условие

f_мах ≤ f_норм.. (1.22)

Метод расчета по предельным состояниям, основанный на глубоком изучении степени нагружения и экспериментально-теоретическом исследовании действительной несущей способности конструкций, обеспечивает бóльшую степень их надежности, чем метод допускаемых напряжений или метод разрушающих нагрузок. Широкие перспективы для снижения материалоемкости конструкций открывает систематизация статистических данных по вопросам технологии изготовления (возведения) и эксплуатации конструкций (сооружений).

Если необходимо добиться наименьших изменений формы конструкции, то производится расчет по допускаемым перемещениям. Это не исключает и одновременной проверки системы на прочность по напряжениям.

В случае расчета конструкции по допускаемым перемещениям необходимо удовлетворять условию

где и - максимальное и допускаемое значения перемещения.

Вопросы для самопроверки

- В чем заключаются задачи курса «Сопротивление материалов»?

- Назовите выдающихся русских ученых в области прочности материалов?

- Что называют прочностью, жесткостью, устойчивостью детали?

- Что такое расчетная схема объекта?

- Укажите геометрические признаки стержня, оболочки и массивного тела.

- Какой брус называется призматическим?

- Изложите основные требования при проектировании машин и сооружений?

- Какие силы в сопротивлении материалов считают внешними? Какие силы являются внутренними?

- Что называют внутренними усилиями?

- Как определяют внутренние усилия?

- Какие правила знаков приняты для каждого из внутренних усилий?

- Являются ли реакции опор внутренними усилиями?

- Возникают ли внутренние силы в ненагруженном теле? в недеформированном теле?

- В чем суть метода сечений?

- Что мы называем отсеченной частью тела?

- Почему обе отсеченные части, на которые разделено тело некоторым произвольным сечением, равноценны с точки зрения определения внутренних сил, действующих в этом сечении?

- От чего зависят знаки внутренних силовых факторов: от характера их действия на отсеченную часть или от направления координатных осей?

- Какая особая точка в сечении принимается за центр приведения внутренних сил?

- Какую из отсеченных частей более целесообразно рассматривать в равновесии? Почему?

- Какие внутренние усилия возникают в поперечных сечениях бруса в случае действия на него плоской системы сил?

- Как вычисляются продольная и поперечная силы в сечении?

- Как вычисляется изгибающий момент?

- Какие типы опор применяются для закрепления балок к основанию?

- Какие внешние реактивные силы возникают в различных опорах?

- Какие уравнения используют для определения опорных реакций?

- Как проверить правильность определения реакций?

- Какими методами определяют внешние силы? Как называют метод для определения внутренних сил?

- Как классифицируются нагрузки, действующие на части машин и сооружений?

- Что такое сосредоточенная сила, распределенная нагрузка и момент?

- Какие нагрузки принято считать сосредоточенными?

- Какое тело называют брусом? Нарисуйте любой брус и укажите ось бруса и его поперечное сечение?

- Какие усилия включают в себя полная система внешних сил?

- Как в сопротивлении материалов располагают систему координат?

- Что в сопротивлении материалов называют внутренними силовыми факторами?

- Перечислите внутренние силовые факторы.

- Перечислите внутренние силовые факторы сечения бруса для общего случая, плоской задачи, линейной задачи?

- Как определяются внутренние силовые факторы через внешние силы?

- Запишите систему уравнений, используемую при определении внутренних силовых факторов в сечении?

- Как обозначается и как определяется продольная сила в сечении?

- Как обозначаются и как определяются поперечные силы?

- Как обозначаются и определяются изгибающие и крутящие моменты?

- Какие деформации вызываются каждым из внутренних силовых факторов?

- Поясните суть метода сечений.

- Чему равен главный вектор и главный момент внутренних сил?

- Как определяют внутренние силовые факторы?

- Какие основные виды деформаций вызываются внешними силами?

- Типы деформаций.

- Какие возможны виды деформации тела и как они связаны с внутренними силовыми факторами?

- В чём заключается количественная оценка деформаций?

- Перечислите простые виды сопротивление стержня.

- Дайте определение понятия «напряжения» и какие виды напряжения вы знаете?

- В каких единицах измеряются напряжения?

- Чем отличаются нормальные напряжения от касательных?

- Что оценивается величиной напряжений?

- Что такое равнопрочная конструкция?

- Как связаны напряжения в сечении с внутренними силовыми факторами?

- Что называется напряжением? Какая у него размерность?

- Какое напряжение называется нормальным и какое касательным?

- Как связаны напряжения в сечении с внутренними силовыми факторами?

- Как по отношению к площадке направлены нормальные и касательные напряжения? Как они обозначаются?

- Какие напряжения возникают в поперечном сечении при действии продольных сил?

- Какие напряжения возникают при действии поперечных сил?

- Как выражается размерность напряжения в системе СИ и в технической системе?

- Что называется деформацией? Какие деформации называют упругими?

- Какие деформации относятся к простым?

- Какие гипотезы используются при изучении курса «Сопротивление материалов»?

- Что следует понимать под напряженным состоянием в точке?

- Поясните, что такое линейная и угловая деформация.

- Сформулируйте закон Гука и принцип суперпозиции.

- Перечислите основные допущения сопротивления материалов.

- Дайте формулировку принципа Сен-Венана?

- Что называется абсолютным удлинением?

- Что понимается под гипотезой плоских сечений?

- В чем сущность и значение для расчетов принципа малости деформаций?

- В чем заключается принцип независимости действия сил (суперпозиции), при каких условиях этот принцип имеет место, для каких целей применяется?

- Как формулируется закон Гука?

- Что характеризует модуль упругости первого рода? Какова его размерность?

- Что называют абсолютной и относительной линейными деформациями?

- Что такое коэффициент Пуассона?

- Как записывается закон Гука для растяжения (сжатия)?

- В чем различия между деформациями и перемещениями?

- Как определить потенциальную энергию деформации при растяжении (сжатии)?

- Что называют прочностью, пластичностью, упругостью, твердостью материала?

- Что называют пределом пропорциональности, упругости, текучести, прочности (временным сопротивлением) материала?

- Чем характеризуют пластичность материала? По какому признаку материалы делят на хрупкие и пластичные?

- Что такое принцип начальных размеров?

- В чем заключается гипотеза о сплошности и изотропности материалов? Какие тела называются анизотропными?

- Дайте определение нормативного (R_н) и расчетного (R) сопротивления и опишите, как они устанавливаются?

- Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?

- В чем различие между предельным и допускаемым напряжениями?

- Что называется относительной продольной и относительной поперечной деформацией? Для чего они определяются?

- Какие напряжения считают предельными для материалов?

- Что представляет собой коэффициент запаса прочности, с какой целью и как его назначают?

- В чем заключается условие прочности элемента конструкции?

- Как составляют условие жесткости для элементов конструкций?

- В чем основное назначение определения твердости готовых деталей?

- Какие напряжения считают предельными для материалов?

- Что представляет собой коэффициент запаса прочности, с какой целью и как его назначают?

- В чем заключается условие прочности элемента конструкции?

- Что представляет собой допускаемое напряжение? Как его определяют?

- Как составляют условие жесткости для элементов конструкции?

- С какой целью проводятся механические испытания материалов? Какие напряжения являются опасными для пластичных и хрупких материалов?

- Что называется допускаемым напряжением? Как оно выбирается для пластичных и хрупких материалов?

- Что называется коэффициентом запаса прочности и от каких основных факторов зависит его величина?

- Какие три типа расчетов встречаются при расчете прочности конструкций? Напишите условия прочности при растяжении для каждого из этих видов задач?

- Перечислите основные принципы расчета инженерных конструкций.

- Рабочее напряжение, возникающее в детали, равно 160 МПа, а опасное (предельное) напряжение для материала детали σ_пред=320 МПа. Определить коэффициент запаса прочности?

Тесты для самоконтроля

- Сопротивление материалов – это наука о __________ элементов конструкций.

1. прочности, жесткости и устойчивости

2. прочности, жесткости и однородности

3. жесткости, устойчивости и пластичности

4. прочности, устойчивости и сплошности.

- В сопротивлении материалов относительно структуры и свойств материала принимаются гипотезы …

1. изотропности, идеальной упругости и пластичности

2. устойчивости, жесткости и прочности

3. сплошности, однородности и линейности

4. сплошности, однородности, изотропности и идеальной упругости

Решение: Решение задач с учетом всех свойств реального материала невозможно в силу их очевидной неисчерпаемости.
Гипотезы сплошности, однородности, изотропности и идеальной упругости позволяют упростить задачи, решаемые в курсе «Сопротивление материалов», и довести их до числового результата.

- Что мы называем прочностью: способность

1. Сопротивляться внешним нагрузкам, не разрушаясь?

2. Сопротивляться внешним нагрузкам, без видимых деформаций?

3. Сопротивляться большим деформациям при малом изменении нагрузки?

- Что мы называем жесткостью: способность

1. Сопротивляться внешним нагрузкам, не разрушаясь?

2. Сопротивляться внешним нагрузкам, без видимых деформаций?

3. Сопротивляться большим деформациям при малом изменении нагрузки?

- Что мы называем устойчивостью: способность

1. Сопротивляться внешним нагрузкам, не разрушаясь?

2. Сопротивляться внешним нагрузкам, без видимых деформаций?

3. Сопротивляться большим деформациям при малом изменении нагрузки?

- Способность конструкций и деталей машин выдерживать рабочие нагрузки без разрушения и пластических деформаций называется

1. прочностью;

2. жесткостью;

3. устойчивостью.

- Способность конструкций и деталей машин выдерживать рабочие нагрузки без значительных упругих деформаций, которые могут нарушить их нормальную работу, называется

1. прочностью;

2. жесткостью;

3. устойчивостью.

- Способность конструкции и её элементов сохранять определенную начальную форму упругого равновесия под нагрузкой называется

1. прочностью;

2. жесткостью;

3. устойчивостью.

- Способность материальных тел восстанавливать первоначальную форму и размеры после снятия нагрузки называется

1. упругостью;

2. пластичностью;

3. материальной однородностью;

4. изотропностью.

- Способность материальных тел не восстанавливать первоначальную форму и размеры после снятия нагрузки называется

1. упругостью;

2. пластичностью;

3. материальной однородностью;

4. изотропностью.

- Способность материала проявлять одинаковые свойства во всех точках называется

1. упругостью;

2. пластичностью;

3. материальной однородностью;

4. изотропностью.

- Способность материала проявлять одинаковые свойства во всех направлениях называется

1. упругостью;

2. пластичностью;

3. материальной однородностью;

4. изотропностью.

- Какой вид деформации считается упругим? Если образец после удаления нагрузки:

1. Частично восстанавливает размеры и форму.

2. Не восстанавливет размеры и форму.

3. Полностью восстанавливает размеры и форму.

- Какая из составляющих расчетной схемы является необязательной?

1. Геометрия объекта.

2. Характеристики материала.

3. Стоимость.

4. Нагрузки.

- Какая из перечисленных гипотез о физических свойствах конструкционных материалов является лишней?

1. Гипотеза сплошности.

2. Гипотеза однородности.

3. Гипотеза об абсолютной жесткости.

4. Гипотеза об абсолютной упругости.

5. Гипотеза об изотропности.

6. Гипотеза о естественной ненапряженности.

- Какой из методов применяют для определения внутренних силовых факторов?

1. Метод Мора.

2. Метод сечений.

3. Метод перемещений.

4. Метод фокусных отношений.

- Какой из типов изгиба является простым видом деформации?

1. Косой изгиб.

2. Плоский поперечный изгиб.

3. Продольный изгиб.

4. Продольно-поперечный изгиб.

- Какой из приведенных видов деформаций не является простым?

1.Сдвиг.

2. Плоский поперечный изгиб.

3. Осевое растяжение и сжатие.

4. Внецентренное растяжение и сжатие.

5. Кручение.

- Внутренними силами называются …

1. дополнительные силы взаимодействия между частицами материала, возникающие в процессе нагружения тела;

2. силы взаимодействия между частями ненагруженного тела;

3. силы межатомного и межмолекулярного сцепления тела в его естественном состоянии;

4. три силы и три момента в поперечном сечении нагруженного стержня.

- Каким фактором являются поперечная сила, изгибающий момент, продольная сила, крутящий момент?

1. Внешним.

2. Внутренним.

- Какой из внутренних силовых факторов не возникает при изгибе?

1. Поперечная сила.

2. Изгибающий момент.

3. Продольная сила.

- При каком из видов деформации возникает продольная сила?

1. Изгиб.

2. Кручение.

3. Сдвиг.

4. Осевое растяжение и сжатие.

- Что является интенсивностью внутренних усилий?

1. Деформация.

2. Напряжение.

3. Перемещение.

- Чем является напряжение в точке?

1. Вектором.

2. Тензором.

3. Скаляром.

- В каких единицах измеряются механические напряжения?

1. В амперах.

2. В вольтах.

3. В паскалях.

4. В радианах.

- В нагруженном теле внутренняя сила, приходящаяся на единицу площади какого-либо сечения, называется ______________ в данной точке на данной площадке.

1. продольной силой;

2. поперечной силой;

3. напряжением;

4. критической силой;

5. сосредоточенной силой.

- Как называется проекция вектора полного напряжения на плоскость сечения?

1. нормальное напряжение;

2. касательное напряжение;

3. главное напряжение.

- Как называется проекция вектора полного напряжения на нормаль сечения?

1. нормальное напряжение;

2. касательное напряжение;

3. главное напряжение.

- Какой характеристикой функции напряжения являются внутренние силовые факторы?

1. Дифференциальной.

2. Интегральной.

- Интегральной характеристикой каких напряжений является поперечная сила?

1. Нормальных.

2. Касательных.

- При каком виде деформации отсутствуют в поперечных сечениях касательные напряжения?

1. Сдвиг.

2. Кручение.

3. Плоский поперечный изгиб.

4. Осевое растяжение и сжатие.

- При каком виде простой деформации отсутствуют в поперечных сечениях нормальные напряжения?

1. Кручение.

2. Плоский поперечный изгиб.

3. Осевое растяжение и сжатие.

- Какой внутренний силовой фактор является определяющим при плоском поперечном изгибе?

1. Поперечная сила.

2. Крутящий момент.

3. Продольная сила.

4. Изгибающий момент.

- Способность твердого тела сопротивляться внешним нагрузкам, не разрушаясь (способность сопротивляться разрушению), называется…

1. устойчивостью;

2. прочностью;

3. жесткостью;

4. выносливостью.

- Принцип, утверждающий, что результат действия системы сил равен сумме результатов действий каждой силы в отдельности, называется…

1. принципом начальных размеров;

2. принципом Сен-Вена;

3. все утверждения верны;

4. принципом независимости действия сил.

- Принцип, утверждающий, что при упругих деформациях в большинстве случаев перемещения, возникающие в конструкции, малы и форма конструкции при этом изменяется незначительно, называется…

1. принципом независимости действия сил;

2. принципом начальных размеров;

3. принципом суперпозиции;

4. принципом Сен-Вена.

- Если не учитывается конкретная структура материала (зернистая, кристаллическая и др.), и считается, что материал непрерывно заполняет весь объем элемента конструкции, то материал обладает свойством…

1. однородности и изотропности;

2. изотропности;

3. анизотропности;

4. сплошности.

- В модели формы при расчетах прочностной надежности вводят упрощение в геометрию элементов конструкций, приводя их к схеме…

1. кривого стержня или тонкостенной трубы;

2. шарнирно-стержневой системы и ломаного стержня;

3. стержневой системы и статически неопределимой рамы;

4. стержня (бруса), пластинки, оболочки и массива (пространственного тела).

- Тело, длина которого l существенно превышает характерные размеры поперечного сечения (ширины и высоты) b и h, называется…

1. пластинкой;

2. массивом (пространственным телом);

3. стержнем (брусом);

4. оболочкой.

- Величины, служащие мерой механического действия одного материального тела на другое, называются…

1. внутренними силовыми факторами;

2. внутренними силами;

3. напряжениями;

4. внешними силами (нагрузками).

- Компонент вектора полного напряжения р, действующего в некоторой точке сечения тела, определяемый проекцией вектора р на плоскость сечения, называется…

1. напряженным состоянием;

2. нормальным напряжением σ;

3. касательным напряжением τ;

4. поперечной силой.

- Проекция главного вектора R внутренних сил на ось (Х или У), лежащую в плоскости сечения, называется…

1. напряженным состоянием;

2. поперечной силой Q_x (или Q_y);

3. продольной силой N;

4. касательным напряжением.

- Момент внутренних сил, действующих в поперечном сечении стержня относительно оси Х (или У), лежащей в плоскости сечения, называется…

1. изгибающим моментом M_x (или M_y);

2. крутящим моментом M_x;

3. главным моментом;

4. моментом силы относительно оси.

- Какая из интегральных зависимостей используется для вывода формулы для нормальных напряжений?

1.

2.

3.

4.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00