Главная
Лекция 9 (продолжение). Примеры решения по устойчивости сжатых стержней
Определение грузоподъемности центрально-сжатого стержня из
условия устойчивости
Пример 1.
Стержень,
показанный на рис. 1, а,
загружен сжимающей силой F. Поперечное сечение
стержня, состоящее из двух швеллеров № 30 и двух планок, соединенных со
швеллерами четырьмя болтами, изображено на рис. 1, б. Размер планок 400х12 мм, диаметр болтов 20 мм. Материал – сталь
С235 с ![]() .
.
Требуется:
1) найти значение критической нагрузки;
2) определить допускаемую нагрузку так, чтобы выполнялись условия устойчивости и прочности стержня;
3) вычислить нормируемый коэффициент запаса устойчивости.
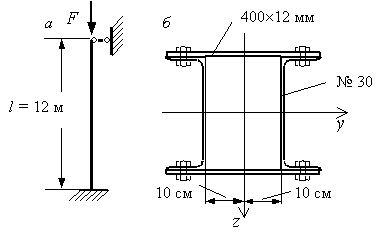
Рис.1
Решение.
Прежде всего,
найдем моменты инерции поперечного сечения относительно главных центральных
осей. Сечение имеет две оси симметрии (оси y и z на
рис. б), поэтому эти оси и будут
главными центральными осями инерции сечения. Моменты инерции относительно этих
осей определяем, используя данные из сортамента прокатной стали и формулы ![]() ,
, ![]() :
:
![]()
![]()
Минимальным оказался момент инерции относительно оси z. Определяем площадь сечения
![]()
и минимальный
радиус инерции по формулам ![]() ,
, ![]() и выбрав минимальный
из двух:
и выбрав минимальный
из двух:
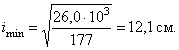
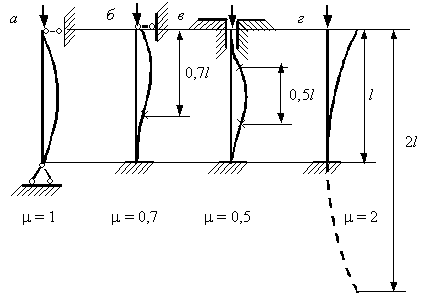
Рис.2
Теперь можно
найти гибкость стержня. Для заданного условия закрепления стержня в
соответствии с рис. 2 коэффициент ![]() . Тогда по формуле
. Тогда по формуле ![]()
![]()
Сравним
величину полученной гибкости стержня с характеристиками ![]() и
и ![]() для материала сталь
С235. Для стали С235
для материала сталь
С235. Для стали С235
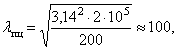
![]() по таблице в (справочные данные). Таким образом,
по таблице в (справочные данные). Таким образом, ![]() и для определения
критической силы следует использовать формулу Ясинского
и для определения
критической силы следует использовать формулу Ясинского ![]() :
:
![]()
Значения коэффициентов a и b в формуле Ясинского взяты из таблицы в (справочные данные) и переведены из МПа в кН/см2.
Найдем
допускаемую нагрузку из условия устойчивости по формуле ![]() . Для определения коэффициента
. Для определения коэффициента ![]() используем таблицу в (справочные данные). Интерполируем значения
используем таблицу в (справочные данные). Интерполируем значения ![]() , заданные в таблице:
, заданные в таблице: ![]() соответствует
соответствует ![]() ,
, ![]() . Тогда
гибкости
. Тогда
гибкости ![]() рассматриваемого
стержня соответствует
рассматриваемого
стержня соответствует ![]() . Значение допускаемой нагрузки
. Значение допускаемой нагрузки
![]()
Проверим,
удовлетворяет ли найденная допускаемая нагрузка условию прочности ![]() . Вычислим площадь нетто, уменьшив полную площадь сечения на
площадь, занимаемую четырьмя отверстиями под болты (при выполнении
расчетно-проектировочной работы студенту предлагается условно принять площадь
ослаблений, составляющую 15% от полной площади):
. Вычислим площадь нетто, уменьшив полную площадь сечения на
площадь, занимаемую четырьмя отверстиями под болты (при выполнении
расчетно-проектировочной работы студенту предлагается условно принять площадь
ослаблений, составляющую 15% от полной площади):
![]()
Тогда условие прочности
![]()
выполняется.
В заключение найдем нормируемый коэффициент запаса устойчивости по формуле:
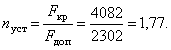
Коэффициент запаса устойчивости
находится в пределах ![]() .
.
Пример 2.
Определить
критическую нагрузку для сжатого стального стержня, имеющего прямоугольное
поперечное сечение 4![]() 6 см. Концы стержня
шарнирно закреплены. Длина стержня l = 0,8
м.
6 см. Концы стержня
шарнирно закреплены. Длина стержня l = 0,8
м.
Решение.
Вычисляем минимальный радиус инерции поперечного сечения стержня:
![]()
Согласно
рисунку принимаем ![]()
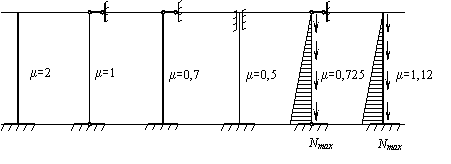
Находим значение гибкости сжатого стержня:
![]()
Так как ![]() , то для вычисления критического напряжения
, то для вычисления критического напряжения ![]() используем формулу
Ясинского
используем формулу
Ясинского ![]() предварительно выписав
из таблицы (справочные данные) коэффициенты а = 310 МПа, в = 1,14 МПа, с = 0:
предварительно выписав
из таблицы (справочные данные) коэффициенты а = 310 МПа, в = 1,14 МПа, с = 0:
![]()
и тогда Fcr =![]()
![]() 0,55 мН = 550 кН.
0,55 мН = 550 кН.
Пример 3.
Определить
величину критической силы, критического напряжения для стойки длиной l = 4 м, один конец которой жестко защемлен, а другой шарнирно оперт.
Материал стойки – сталь с ![]() Поперечное сечение
стойки показано на рисунке.
Поперечное сечение
стойки показано на рисунке.
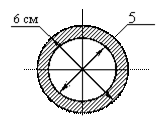
Решение.
Согласно
рисунку, приведенному в предыдущем примере принимаем ![]() Вычисляем осевой
момент инерции кольцевого поперечного сечения:
Вычисляем осевой
момент инерции кольцевого поперечного сечения:
![]()
а затем и радиус инерции поперечного сечения:
![]()
Определяем гибкость сжатого стержня:
![]()
Таким образом,
критическую силу вычисляем по формуле Эйлера ![]() :
:
![]()
а критическое
напряжение по формуле ![]() :
:
![]()
Пример 4.
Определить
критическую силу для деревянной стойки прямоугольного поперечного сечения 10![]() 20 см и длиной 8 м, если оба конца стойки шарнирно
закреплены. Материал стойки – сосна с модулем продольной упругости Е =
20 см и длиной 8 м, если оба конца стойки шарнирно
закреплены. Материал стойки – сосна с модулем продольной упругости Е = ![]() МПа.
МПа.
Решение.
Согласно
рисунку, приведенному в предыдущем примере принимаем ![]()
Определяем
гибкость стойки 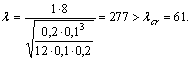
Следовательно,
для определения критической силы будем применять формулу Эйлера ![]() :
:
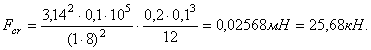
Ответ:
![]() = 25,68 кН.
= 25,68 кН.
Пример 5.
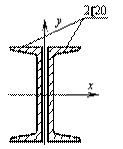
Составной
стальной стержень длиной 5 м состоит из двух швеллеров № 20, соединенных
вплотную (см. рис.). Определить допустимую сжимающую нагрузку, если оба конца
стержня шарнирно закреплены. Материал швеллеров – сталь с ![]()
Решение.
Расчет
составных элементов из уголков, швеллеров и т.п., соединенных вплотную или
через прокладки, следует выполнять как сплошностенчатых. Находим ![]()
![]()
![]()
Определяем
гибкость сжатого составного элемента по формуле ![]() :
:
![]() а из таблицы (справочные данные) находим
а из таблицы (справочные данные) находим ![]() = 0,2284. И, наконец,
из формулы
= 0,2284. И, наконец,
из формулы ![]() определяем при
определяем при ![]() :
:
![]()
Для сравнения
найдем критическую силу для рассматриваемой сжатой стальной стойки (![]() ). Имеем
). Имеем ![]() следовательно,
используем формулу Эйлера
следовательно,
используем формулу Эйлера ![]() :
:
![]()
Пример 6.
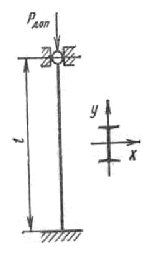
Определить допускаемую нагрузку для стойки (см. рис.), выполненной из двутавра №18, в случаях l=4 м и l=2,5 м, принимая запас устойчивости ny=2,5.
Данные для сечения двутавра № 18: площадь F=30,6 см2, imin=iy=2,0 см, Imin=Iy=122 см4.
Решение.
Для материала
стоек ![]() =100. Гибкость первой стойки
=100. Гибкость первой стойки ![]() .
.
Поэтому для определения критической силы надо воспользоваться формулой Эйлера, а допускаемую нагрузку определить по формуле:
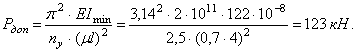
Гибкость
второй стойки ![]()
Следовательно,
выпучивание стойки происходит при ![]() и для определения
допускаемой нагрузки можно воспользоваться формулой
и для определения
допускаемой нагрузки можно воспользоваться формулой
![]()
Отсюда
![]()
Пример 7.
Определить
допускаемое значение силы ![]() из расчета на
устойчивость стержня при заданном коэффициенте запаса устойчивости
из расчета на
устойчивость стержня при заданном коэффициенте запаса устойчивости ![]() . Длина стержня l=1,2 м, материал Ст.
30. Закрепление и размеры
. Длина стержня l=1,2 м, материал Ст.
30. Закрепление и размеры ![]() сечения стержня
показаны на рисунке при
сечения стержня
показаны на рисунке при ![]()
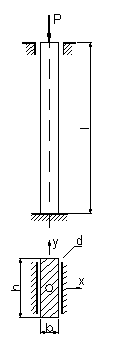
Решение.
Рассмотрим
сначала определение моментов ![]() и радиусов
и радиусов ![]() инерции данной фигуры, которая имеет две оси
симметрии
инерции данной фигуры, которая имеет две оси
симметрии ![]() , которые и являются главными осями инерции. Главные моменты
инерции
, которые и являются главными осями инерции. Главные моменты
инерции ![]() определяются по
формулам
определяются по
формулам
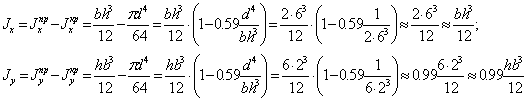
Тогда радиусы инерции определяются так:
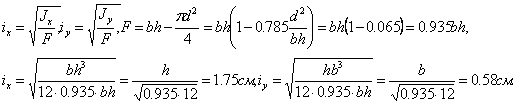
Коэффициенты
приведенной длины ![]()
Гибкость стержня в двух плоскостях находятся (относительно осей x , y соответственно):
![]()
Имеем
![]()
Тогда критическая сила определяется по формуле Эйлера
![]()
Допускаемое значение нагрузки
равно ![]() .
.
Указание. Если заданная фигура сечения имеет одну ось симметрии, то необходимо определить положение центра тяжести и применить формулу параллельного переноса
![]() .
.
Пример 8.
Стальной
стержень длиной ![]() двутаврового сечения
№18, шарнирно закреплённый на одном и жёстко на другом краях, сжимается силами Р. Требуется определить допускаемое и
критическое значения силы Р, если
двутаврового сечения
№18, шарнирно закреплённый на одном и жёстко на другом краях, сжимается силами Р. Требуется определить допускаемое и
критическое значения силы Р, если ![]()
Решение.
Из сортамента
стального проката для двутавра №18 находим F =
23,4 см2, ![]() Коэффициент приведения
длины Ясинского для данного типа закрепления
Коэффициент приведения
длины Ясинского для данного типа закрепления ![]() гибкость стержня
гибкость стержня ![]()
Так как ![]() то критическая сила
может быть определена по формуле Эйлера:
то критическая сила
может быть определена по формуле Эйлера:
![]()
По таблице
коэффициентов ![]() после интерполяции
находим
после интерполяции
находим ![]() Вычисляем допускаемое
значение внешней силы:
Вычисляем допускаемое
значение внешней силы:
![]()
Коэффициент
запаса на устойчивость ![]()
Если принять
длину ![]() , то
, то ![]() В этом случае для
определения критической силы использовать формулу Эйлера нельзя. Воспользуемся
формулой Джонсона:
В этом случае для
определения критической силы использовать формулу Эйлера нельзя. Воспользуемся
формулой Джонсона:
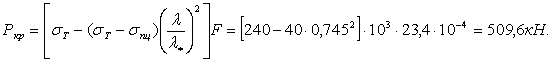
Допустимая нагрузка:
![]()
Коэффициент
запаса ![]()
Если воспользоваться формулой Ясинского, то
![]()
Коэффициент
запаса: ![]()
Пример 9.
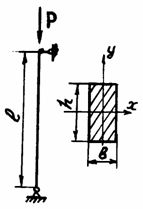
Определить критическую силу для стального стержня
(![]() МПа) прямоугольного сечения (см. рис.), если размеры
сечения: b=0,06 м, h =0,1 м, длина стержня l=3,5
м.
МПа) прямоугольного сечения (см. рис.), если размеры
сечения: b=0,06 м, h =0,1 м, длина стержня l=3,5
м.
Решение.
Определяем гибкость по формуле:
![]() .
.
Вычисляем
![]()
Коэффициент приведения длины ![]() =1.
=1.
Тогда ![]() .
.
Вычисляем предельную гибкость для стали:
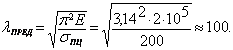
Так как ![]() , то критическую силу надо считать по формуле Эйлера:
, то критическую силу надо считать по формуле Эйлера:
![]()
где ![]()
Расширим эту задачу и определим критическое
напряжение:
![]()
Таким
образом, при гибкости стержня ![]() =202 критическим оказалось напряжение, не только значительно
меньшее предела пропорциональности (
=202 критическим оказалось напряжение, не только значительно
меньшее предела пропорциональности (![]() =200 МПа), но в три с лишним раза меньше допускаемого напряжения
(
=200 МПа), но в три с лишним раза меньше допускаемого напряжения
(![]() =
160 МПа).
=
160 МПа).
Пример 10.
Вертикальный
стальной стержень (марка стали Ст. 3),
поперечное сечение которого показано на рисунке, сжимается с торца
консервативной силой P. Длина стержня ![]() м,
м, ![]() см.
см.
![]()
![]()
![]()
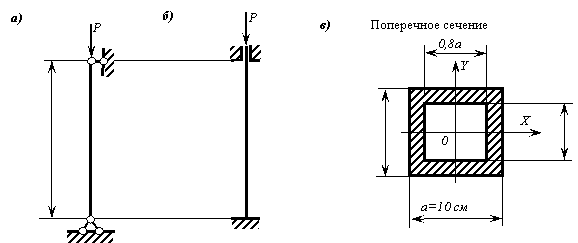
Определить
значение критической и допускаемой нагрузки. Вычислить коэффициент запаса
устойчивости стержня ![]() . Допускаемое
напряжение
. Допускаемое
напряжение ![]() кН/см2,
модуль Юнга
кН/см2,
модуль Юнга ![]() кН/см2.
Решение задачи получить для двух вариантов закрепления концов стержня, когда
оба конца шарнирно оперты (
кН/см2.
Решение задачи получить для двух вариантов закрепления концов стержня, когда
оба конца шарнирно оперты (![]() ) и оба конца жестко защемлены (
) и оба конца жестко защемлены (![]() ).
).
Решение.
1. Определяем
геометрические характеристики поперечного сечения стержня.
Площадь
![]() см2.
см2.
Минимальный
осевой момент инерции
![]() см4.
см4.
Минимальный
радиус инерции поперечного сечения стержня
![]() см.
см.
2. Вычисляем
гибкость стержня ![]() .
.
Для случая,
когда оба конца стержня шарнирно оперты:
![]() .
.
Если оба
конца стержня жестко защемлены, то
![]() .
.
3. Определяем
коэффициент уменьшения основного допускаемого напряжения ![]() .
.
Для случая,
когда оба конца стержня шарнирно оперты, линейной интерполяцией находим, что
при гибкости ![]() коэффициент уменьшения
основного допускаемого напряжения
коэффициент уменьшения
основного допускаемого напряжения ![]() .
.
Если оба
конца стержня жестко защемлены, гибкости ![]() соответствует
соответствует ![]() .
.
4. Определяем
допускаемую нагрузку.
Условие
устойчивости стержня имеет вид:
![]() .
.
Отсюда,
допускаемая нагрузка равна ![]() .
.
Для случая,
когда оба конца стержня шарнирно оперты, имеем
![]() кН.
кН.
Если же оба
конца стержня жестко защемлены, получим
![]() кН.
кН.
5. Вычисляем
критическую нагрузку.
Критическую
нагрузку для шарнирно опертого по концам стержня вычисляем по формуле Эйлера, поскольку гибкость стержня
больше предельного значения: ![]() . Тогда
. Тогда
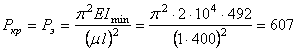 кН.
кН.
Для случая,
когда оба конца стержня жестко защемлены, гибкость ![]() . Поэтому критическую нагрузку определяем по двум формулам:
по формуле Ясинского
. Поэтому критическую нагрузку определяем по двум формулам:
по формуле Ясинского
![]() ,
,
где a и b –
эмпирические коэффициенты, и по формуле
![]() ,
,
где ![]() – предел текучести. В
результате принимаем меньшее из полученных по этим формулам значение
критической нагрузки.
– предел текучести. В
результате принимаем меньшее из полученных по этим формулам значение
критической нагрузки.
Для стали марки Ст. 3 ![]() кН/см2;
кН/см2; ![]() кН/см2;
кН/см2; ![]() кН/см2.
Тогда по первой формуле найдем
кН/см2.
Тогда по первой формуле найдем
![]() кН,
кН,
а по второй –
![]() кН.
кН.
Таким
образом, для стержня, концы которого жестко защемлены, ![]() кН.
кН.
6. По формуле
![]() вычисляем коэффициент
запаса устойчивости стержня.
вычисляем коэффициент
запаса устойчивости стержня.
Для случая,
когда оба конца стержня шарнирно оперты, имеем
![]() .
.
Если же оба
конца стержня жестко защемлены, получим
![]() .
.
Рекомендуемые значения коэффициента
запаса устойчивости для стальных стержней следующие ![]() .
.
Таким
образом, оба найденных нами значения коэффициента запаса устойчивости находятся
в рекомендуемых пределах.
Пример 11.
Для составной
центрально сжатой стальной стойки (см. рис.), состоящей из двух неравнобоких
уголков 75x50x6 мм, требуется:
1. Определить
критическую и допускаемую нагрузки (сталь Ст. 3).
2. Вычислить коэффициент запаса устойчивости.
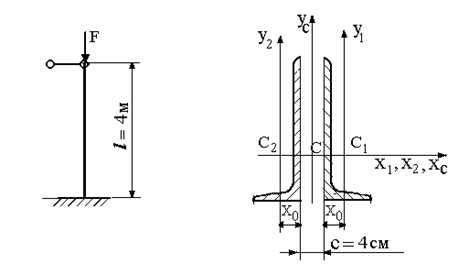
а)
б)
Решение.
Из сортамента
ГОСТ 8510 – 89 для одного уголка выписываем:
Jx=40,9 см4; Jy = 14,6 см4; А = 7,25 см; Х0
= 1,21 см; ix = 2,38 см; iy = 1,42 см.
Определяем
главные центральные моменты инерции и радиусы инерции (рис. б):
![]() ;
; 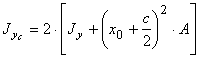 ;
;
![]() ,(где ix –
из сортамента), т.е. ix = 2,38 см = 2,38×10-2
м;
,(где ix –
из сортамента), т.е. ix = 2,38 см = 2,38×10-2
м;
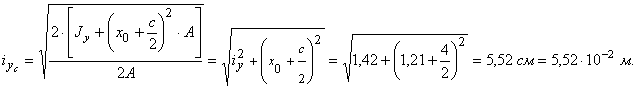
Сравнивая
значения ix и iy видим что imin = ix = 2,38×10-2 м.
Вычисляем
гибкость стойки: ![]()
Так как гибкость
стойки ![]() больше предельной
гибкости для стали (
больше предельной
гибкости для стали (![]() =100), то определяем критическую силу по формуле Эйлера:
=100), то определяем критическую силу по формуле Эйлера:
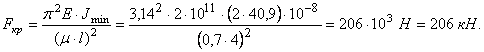
Из таблицы
значений коэффициента понижения основного допускаемого напряжения для
стали Ст 3 при
расчетной гибкости![]() = 118 имеем:
= 118 имеем:
при ![]() = 110
= 110 ![]() = 0,52;
= 0,52;
при ![]() =120
=120 ![]() = 0,45.
= 0,45.
Используя формулу
линейной интерполяции для
гибкости
![]() = 118 получим:
= 118 получим: 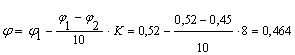 ,
,
где K = 8 - число единиц в
значении гибкости ![]() = 118.
= 118.
Вычисляем
допускаемую нагрузку, принимая ![]() = 160 МПа:
= 160 МПа:
![]()
Для
вычисления коэффициента запаса устойчивости используем формулу: ![]() .
.
Расчет на устойчивость систем с одной или двумя степенями свободы при
помощи уравнений равновесия
Пример 12.
Два бесконечно жестких стержня связаны между собой шарниром (см. рис.) и оперты на упругие пружины, жесткость которых равна k. Определить критическое значение сжимающей силы.
![]()
![]()
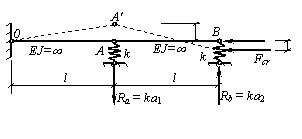
Решение.
Решим поставленную задачу статическим методом при помощи уравнений равновесия для отклоненного состояния. Для этого рассмотрим систему, показанную на рисунке в отклоненном состоянии, т.е. после потери устойчивости. В отклоненном состоянии на упругих опорах возникнут опорные реакции Ra = ka1 и Rb = ka2, где k – жесткость упругих связей (пружин), равная силе, вызывающей единицу деформации упругой связи (пружины). Будем считать, что k – известная величина. Составим условие равновесия моментов относительно точки О:
![]() ,
,
а после подстановки в полученное выражение значений опорных реакций Ra и Rb получим
![]() .
(1)
.
(1)
Составим также
условие равенства момента нулю в шарнире А/
в отклоненном состоянии:![]() , а после подстановки в полученное выражение значения опорной
реакции Rb получим
, а после подстановки в полученное выражение значения опорной
реакции Rb получим
![]() .
(2)
.
(2)
Таким образом, имеем систему двух уравнений (1), (2) с двумя неизвестными геометрическими параметрами а1 и а2. Полученная система содержит два однородных уравнения и, следовательно, определитель, составленный из коэффициентов при неизвестных а1 и а2, должен быть равен нулю:
![]()
Раскрывая определитель, получим уравнение второй степени
![]()
решения
которого имеют вид: ![]() откуда находим два
значения критической силы: Fcr,1
= 0,38kl и Fcr,2
= 2,63kl. Окончательно принимаем Fcr = 0,38kl как наименьшую
критическую силу, вызывающую потерю устойчивости.
откуда находим два
значения критической силы: Fcr,1
= 0,38kl и Fcr,2
= 2,63kl. Окончательно принимаем Fcr = 0,38kl как наименьшую
критическую силу, вызывающую потерю устойчивости.
Определение критических сил при помощи энергетического
метода
Энергетический метод основан на использовании теоремы Лагранжа – Дирихле о полной потенциальной энергии.
Рассмотрим порядок расчета для энергетического метода:
1. Задаются уравнением новой формы равновесия в виде одного или нескольких членов ряда, удовлетворяющих краевым условиям:
![]()
При выборе функции у кинематические граничные условия (прогибы, углы поворота) должны быть удовлетворены обязательно. Статическим граничным условиям (изгибающим моментам, поперечным силам) удовлетворять не обязательно, однако для получения более точных результатов – крайне желательно. Имеются специальные таблицы для выбора уравнений криволинейной формы равновесия стержня, потерявшего устойчивость. Например, в таблице 2 приведены данные для трех видов стержней.
Таблица 2
|
Схема стойки |
Нижний (левый) конец |
Верхний (правый) конец |
Уравнение криволинейной формы равновесия прямых стержней |
||||
|
y(0) |
y/(0) |
y(l) |
y/(l) |
||||
|
|
0 |
0 |
- |
- |
|
||
|
|
0 |
- |
0 |
- |
|
||
|
|
0 |
- |
0 |
- |
|
||
2. Вычисляем полную потенциальную энергию П системы при переходе из новой формы равновесия в первоначальную:
![]() (1)
(1)
где rii – жесткость упругой
связи, Н/м; ai –
линейная деформация (удлинение или укорочение) упругой связи, Fcr,k –
неизвестное значение критической силы и ![]() – перемещение, на котором критическая сила Fcr,k совершает работу.
– перемещение, на котором критическая сила Fcr,k совершает работу.
Принимая во
внимание дифференциальное уравнение упругой оси балки ![]() и выражение
и выражение ![]() , формулу (1) можно представить в виде:
, формулу (1) можно представить в виде:
![]() (2)
(2)
3. Определяем экстремальное значение потенциальной энергии из уравнений:
![]()
4. Приравнивая детерминант из коэффициентов при параметрах an нулю, определяем критические силы, число которых равно числу параметров an. Если используется точное выражение ординаты у искривленной оси, то получим точное значение критической силы. В основном критические силы получаются несколько завышенными.
Пример 13.
Определить критическую силу для прямого стержня, находящегося в упругой среде с коэффициентом податливости, равным k (см. рис.).
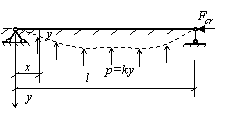
Решение.
Уравнение криволинейной формы равновесия прямого стержня берем из табл. 2 в виде:
![]() .
.
Для вычисления
полной потенциальной энергии по формуле (2) предварительно необходимо вычислить
![]() и
и ![]()
![]()
а затем
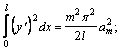
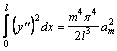 и
и 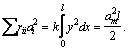
Подставляя полученные значения в формулу (2), находим
![]()
Из последнего выражения определяем
![]() ,
,
где m – число полуволн при потере устойчивости. Значение m, при котором Fcr равна минимальному значению, зависит от коэффициента податливости k упругого основания (Н/м2). При малом k можно принять m = 1.
Продолжим
исследование и предположим, что ![]() тогда
тогда
![]() откуда
откуда![]()
Таким образом,
если ![]() то необходимо
принимать m = 1,
то необходимо
принимать m = 1,
если ![]() , то m > 1.
, то m > 1.
Пример 14.
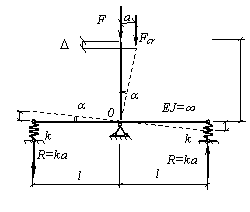
Определить значение критической силы при помощи энергетического метода для абсолютно жесткой системы, изображенной на рисунке. Жесткость двух упругих связей – одинакова и обозначена через k.
![]()
![]()
![]()
Решение.
Пусть система потеряла устойчивость и заняла новое положение. Так как стержни – абсолютно жесткие, то они не будут изгибаться, а останутся прямыми. В результате потери устойчивости на упругих опорах возникнут опорные реакции R = ka, где а – вертикальное отклонение концов горизонтального участка системы. На такое же расстояние а переместится в горизонтальном направлении верхний конец системы вместе с критической силой Fcr, а в вертикальном направлении перемещение верхнего конца системы составит
![]()
Кроме того,
имеем, что ![]() откуда
откуда ![]() Тогда формула (1)
примет вид:
Тогда формула (1)
примет вид:
![]()
![]()
Из последнего
выражения определяем ![]()
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов