Главная
Тестовые
вопросы по теме «Определение перемещений в балках»
- Какое из перемещений поперечных сечений не возникает при плоском изгибе балки?
1. Прогиб.
2. Угол поворота.
3. Угол закручивания.
4. Продольное перемещение.
- Первая производная от прогиба по продольной координате есть:
1. Синус угла поворота сечения?
2. Тангенс угла поворота сечения?
3.Косинус угла поворота сечения?
2. Котангенс угла поворота сечения?
- Каким из уравнений описывается изогнутая ось балки при плоском поперечном изгибе?
1. Алгебраическим.
2. Интегральным.
3. Дифференциальным.
4. Тригонометрическим.
- Какое из уравнений является приближенным (основным) уравнением упругой линии балки?
1) ![]()
2) ![]()
3) ![]()
4) ![]()
- При определении перемещений при плоском изгибе как поступают с основным дифференциальным уравнением упругой линии?
1. Дифференцируют.
2. Раскладывают в ряд.
3. Интегрируют.
4. Потенцируют.
- Сколько раз нужно проинтегрировать основное дифференциальное уравнение упругой линии, чтобы получить выражение для прогиба?
1. Два раза.
2. Три раза.
3. Один раз.
4. Четыре раза.
- Сколько раз нужно проинтегрировать основное дифференциальное уравнение упругой линии, чтобы получить выражение для угла поворота?
1. Два раза.
2. Три раза.
3. Один раз.
4. Четыре раза.
- Что из себя представляет уравнение ![]()
1. Выражение для изгибающего момента M(x).
2. Выражение для поперечной силы Q(x).
3. Выражение для угла поворота 𝜃(x).
4. Выражение для интенсивности распределенной нагрузки q(x).
5. Выражение для прогиба w(x).
- Что из себя представляет уравнение ![]()
1. Выражение для изгибающего момента M(x).
2. Выражение для поперечной силы Q(x).
3. Выражение для угла поворота 𝜃(x).
4. Выражение для интенсивности распределенной нагрузки q(x).
5. Выражение для прогиба v(x).
- Что из себя представляет уравнение ![]()
1. Выражение для изгибающего момента M(x).
2. Выражение для поперечной силы Q(x).
3. Выражение для угла поворота 𝜃(x).
4. Выражение для интенсивности распределенной нагрузки q(x).
5. Выражение для прогиба v(x).
- Что можно определить с помощью выражения ![]()
1. Поперечную силу Q(x).
2. Прогиб v(x).
3. Интенсивность распределенной нагрузки q(x)
4. Угол поворота 𝜃(x).
5. Изгибающий момент M(x).
- Что можно определить с помощью выражения ![]()
1. Поперечную силу Q(x).
2. Прогиб v(x).
3. Интенсивность распределенной нагрузки q(x)
4. Угол поворота 𝜃(x).
5. Изгибающий момент M(x).
- Для определения перемещений при растяжении (сжатии) применяется интеграл…
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- При интегрировании основного дифференциального уравнения упругой линии используют граничные условия. С какой целью?
1. Для определения границ изменения величины изгибающего момента M(x).
2. Для определения границ изменения величины поперечной силы Q(x).
3. Для определения границ изменения величины угла поворота θ(x).
4. Для определения границ изменения величины прогиба v(x).
5. Для определения значений постоянных интегрирования C, D.
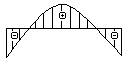
- Какая из эпюр углов поворота
соответствует представленной
на рисунке эпюре изменения прогибов?
![]()
1. 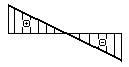
2. 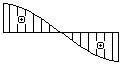
3. 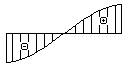
4. 
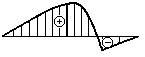
- Какая из эпюр прогибов соответствует
представленной на рисунке эпюре изгибающих моментов?
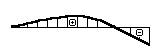
1. 
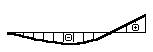
2. 
3. ![]()
4. ![]()
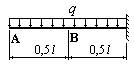
- В сколько раз прогиб в сечении А на конце изображенной на рисунке балки, больше, чем прогиб в сечении В посредине балки?
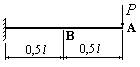
1. В 3 раза.
2. В 3,5 раза.
3. В 2,8 раза.
4. В 3,2 раза.
- В сколько раз угол поворота
сечения А на конце изображенной на рисунке балки больше, чем угол поворота
сечения В посредине балки?
1. В 1,225 раза.
2. В 1,143 раза.
3. В 1,159 раза.
4. В 1,137 раза.
- На каких двух фундаментальных принципах механики
основан общий метод определения перемещений?
1. Принцип Сен-Венана и закон Гука.
2. Принцип суперпозиции и закон всемирного тяготения.
3. Принцип возможных перемещений и закон сохранения энергии.
4. Принцип Даламбера и третий закон Ньютона.
- Как называются группы постоянных сил и соответствующих перемещений, на которых эти силы совершают работу?
1. Сосредоточенные силы и линейные перемещения.
2. Сосредоточенные моменты и угловые перемещения.
3. Крутящие моменты и углы закручивания.
4. Обобщенные силы и обобщенные координаты.
- Какой вид имеет теорема о работе внешних сил (теорема Бетти)?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
- Что из себя представляет выражение:
![]()
1. Работа внешних сил.
2. Потенциальная энергия деформации.
3. Работа внутренних
сил.
4. Полная работа.
- В каком случае сумма работ внешних и внутренних сил на возможных бесконечно малых перемещениях точек системы равна нулю?
1. Если система состоит из независимых тел, свободно перемещающихся одно по отношению к другому.
2. Если система находится под действием неуравновешенных сил.
3. Если система тел находится в равновесии.
4. Если система дел испытывает динамическое
деформирование.
- Что выражает теорема Бетти?
1. Равенство взаимных деформаций.
2. Равенство взаимных напряжений.
3. Равенство взаимных работ.
4. Равенство взаимных перемещений.
- Что выражает теорема Максвелла?
1. Равенство взаимных деформаций.
2. Равенство взаимных напряжений.
3. Равенство взаимных работ.
4. Равенство взаимных перемещений.
- Какой из
общих методов определения перемещений при плоском изгибе представлен формулой:![]()
1. Метод Максвелла.
2. Метод Лагранжа.
3. Метод Кастильяно.
4. Метод Мора.
- Какой из
методов определения перемещений при расчете шарнирных ферм представлен
формулой:![]()
1. Метод Мора.
2. Метод Кастильяно.
3. Метод Лагранжа.
4. Метод Максвелла.
- Содержание какой из теорем
выражает уравнение:![]()
где U – потенциальная энергия деформации, P – обобщенная сила.
1. Теорема Максвелла.
2. Теорема Кастильяно.
3. Теорема Бетти.
4. Теорема Лагранжа.
- Содержание какой из теорем выражает уравнение:
![]()
где U – потенциальная энергия деформации, ∆i – обобщенная координата.
1. Теорема Максвелла.
2. Теорема Кастильяно.
3. Теорема Бетти.
4. Теорема Лагранжа.
- Какой должна быть потенциальная энергия деформаций конструкции в соответствии с теоремой Менабреа?
1. Принимает максимальное значение.
2. Принимает минимальное значение.
3. Равняется нулю.
4. Принимает отрицательное значение.
- Как называется графоаналитический метод определения
перемещений, представленный формулой:
![]()
1. Метод Мора.
2. Метод Кастильяно.
3. Метод Мора-Симпсона.
4. Метод Лагранжа.
- Какое из единичных состояний балки следует принять при определении угла поворота в сечении А по методу Мора-Симпсона для балки, изображенной на рисунке?
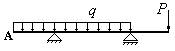
1. ![]()
2. 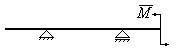
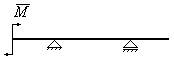
3. 
4. ![]()
-
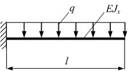
Консольная балка длиной l нагружена равномерно распределенной нагрузкой интенсивности q. Жесткость
поперечного сечения на изгиб EJx по всей длине постоянна. Прогиб свободного конца балки
по абсолютной величине равен …
1) ![]()
2) ![]()
3) ![]()
4) ![]()
- φ – угол поворота, v – прогиб. Сечение 1-1 имеет перемещения…
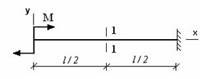
1. v;
2. φ и v;
3. нет перемещений;
4. φ.
- К балке постоянной жёсткости ЕJz в точке С приложена сила F. Величина прогиба в этом сечении Vc ,будет равна:
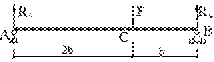
1) ![]()
2) ![]()
3) ![]()
4) ![]()
- Как изменится прогиб балки, если изгибающий момент уменьшить в три раза?
1. уменьшится в три раза;
2. уменьшится в шесть раз;
3. уменьшится в девять раз.
- Балки, изготовленные из стали и чугуна, имеющие одинаковые размеры и устройства опор, подвергаются действию одинаковых сил. Сравните величину максимальных прогибов этих балок?
1. у стальной балки прогиб больше;
2. у чугунной балки прогиб больше;
3. прогиб балок одинаковый.
- Какие перемещения получают поперечные сечения балок при изгибе?
1. линейные;
2. угловые;
3. линейные и угловые.
- Проинтегрировав уравнение EJy’’=M дважды, получим:
1. уравнение углов поворота;
2. кривизну балки;
3. уравнение прогибов;
4. нет правильного ответа.
- Указать выражение, соответствующее жесткости сечения при изгибе.
1. EJ;
2. GА;
3. GJp;
4. ЕА.
- По какой из формул определяется кривизна изогнутой оси
бруса, характеризующая деформацию изгиба.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Приближенное дифференциальное уравнение упругой линии балки имеет вид:
1. ![]() ;
;
2. ![]() ;
;
3. ![]()
4. нет правильного ответа.
- Какая связь между линейными и угловыми перемещениями при изгибе?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Формула максимального прогиба для консольной балки длиной l, нагруженной на конце
силой F:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Формула максимального прогиба для шарнирно опёртой балки длиной l, нагруженной посредине силой F:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Что такое упругая линия балки?
1. кривизна нейтрального слоя;
2. нейтральная линия сечения;
3. изогнутая ось балки;
4. ось балки.
- Условие жёсткости при изгибе:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Формула определения максимального прогиба для шарнирно опёртой балки длиной l, нагруженной равномерно распределённой нагрузкой q:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Балки, изготовленные из стали и чугуна, имеющие одинаковые размеры и устройство опор, подвергаются действию одинаковых сил. Сравните величину максимальных прогибов этих балок.
1. у стальной балки прогиб больше;
2. у чугунной балки прогиб больше;
3. прогиб балок одинаковый.
- Чему равен угол поворота балки в сечении «С»?
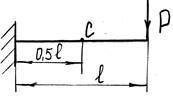
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
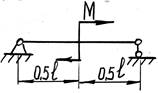
- Чему равен угол поворота в среднем сечении балки?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
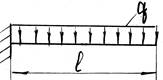
- Чему равен угол поворота свободного конца балки?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
- Чему равен прогиб свободного конца балки?
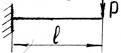
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
- Чему равен прогиб балки в сечении «С»?
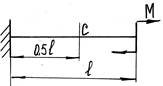
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
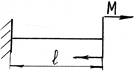
- Чему равен прогиб свободного конца балки?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
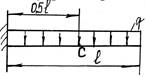
- Чему равен угол поворота балки в сечении «С»?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
4. верный ответ не приведен
- Чему равен угол поворота балки в сечении «С»?

1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
4. верный ответ не приведен
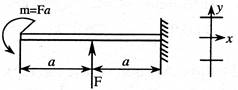
- К балке приложены сила F и момент m.
Подобрать поперечное сечение балки в форме прокатного двутавра из условия
жесткости ![]() ,
если [f] =0,5 см, a= 1 м, E=2∙1011 МПа и F=6 кН.
,
если [f] =0,5 см, a= 1 м, E=2∙1011 МПа и F=6 кН.
1. I
N14; Jx=572 см4;
2. I
N16; Jx=873 см4;
3. I
N18; Jx=1290 см4;
4. I
N20; Jx=1430 см4.
- Определить наибольший прогиб в шарнирно опертой балке пролетом l=2 м, нагруженной посередине силой F=15 кН. Балка имеет квадратное сечение со стороной а=10 см. Модуль упругости материала балки Е=2∙105 МПа.
1. f =
2. f =
3. f =
4. f =
- Определить наибольший прогиб в шарнирно опертой балке пролетом l=2 м, нагруженной посередине силой F=15 кН. Балка имеет круглое сечение D=10 см. Модуль упругости материала балки Е=2∙105 МПа.
1. f =
2. f =
3. f =
4. f =
- Определить наибольший прогиб в шарнирно опертой балке пролетом l=2 м, нагруженной посередине силой F=15 кН. Сечение балки – двутавр №12. Модуль упругости материала балки Е=2∙105 МПа.
1. f =
2. f =
3. f =
4. f =
- Определить максимальный прогиб консоли длиной l = 1 м, нагруженной на свободном конце силой F= 2 кН. Сечение консоли – квадрат со стороной а =15 см. Модуль упругости материала балки Е=104 МПа.
1. f =
2. f =
3. f =
4. f =
- Определить максимальный прогиб консоли длиной l = 1 м, нагруженной на свободном конце силой F =2 кН. Сечение консоли – круг, D =10 см. Модуль упругости материала балки Е=104 МПа.
1. f =
2. f =
3. f =
4. f =
1,6 см.
- Определить прогиб посередине
шарнирно опёртой балки, нагруженной равномерно распределённой нагрузкой q=4 кН/м. Сечение балки прямоугольник b=10 см, h=20 см, l=3 м, Е=104
МПа.
1. f =
0,63 см;
2. f =
3. f =
4. Верны ответы 2 и 3.
- Определить прогиб посередине шарнирно опёртой балки, нагруженной равномерно распределённой нагрузкой q=4 кН/м. Сечение балки – круг D=10 см, l =3 м, Е=104 МПа.
1. f =
2. f =
3. f =
4. Верны ответы 1 и 2.
- Определить прогиб посередине
шарнирно опёртой балки, нагруженной равномерно распределённой нагрузкой q=4 кН/м. Сечение балки – кольцо dхD, α= 0,8,
Е=104 МПа, D=20 cм,
l=3 м.
1. f =
2. f =
3. f =
4. Верны ответы 1 и 3.
- Определить максимальный прогиб консоли длиной l=1 м, нагруженной на конце силой F =2 кН. Сечение консоли – двутавр №10. Модуль упругости материала Е=2∙105 МПа.
1. f =
2. f =
3. f =
4. f =
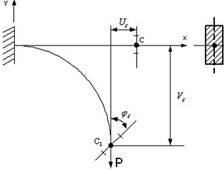
- Балка деформируется под действием силы Р. Сечение С балки имеет линейные Uc, Vc и угловое φС перемещения. Из-за малости можно пренебречь перемещением...
1. Uc и φС
2. φС
3. Uc
4. Vc
- На рисунке показана схема нагружения балки. Форма деформированной оси балки имеет вид...
![]()
1. ![]()
2. ![]()
3. ![]()
4. ![]()
- φ - угол поворота, v - прогиб. Сечение 1-1 имеет перемещения...
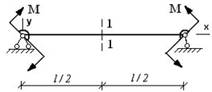
1. v;
2. φ;
3. φ и v.
4. нет перемещений
- φ - угол поворота, v - прогиб. Сечение 1-1 имеет перемещения...
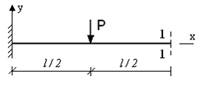
1. v
2. φ
3. φ и v
4. нет перемещений
- φ - угол поворота, v - прогиб. Сечение 1-1 имеет перемещения...
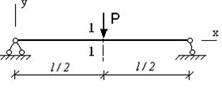
1. v
2. φ
3. φ и v
4. нет перемещений
- Прогиб среднего сечения шарнирно опертой балки (P, l, EIx – известны) равен...
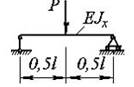
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Максимальный прогиб возникает в сечении...

1. 2-2
2. 1-1
3. 3-3
4. 4-4
- Максимальный прогиб возникает в сечении...
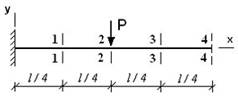
1. 2-2
2. 1-1
3. 3-3
4. 4-4
- Максимальный угол поворота возникает в сечении...
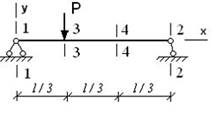
1. 2-2
2. 1-1
3. 3-3
4. 4-4
- Максимальный угол поворота возникает в сечении...
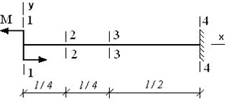
1. 2-2
2. 1-1
3. 3-3
4. 4-4
- Если к однопролетной балке приложить силу F, то при EIx=const угол поворота сечения над левой опорой по модулю |φA| равен:
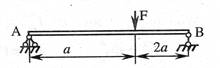
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Однопролетная балка нагружена силой F. Если EIx=const, то угол поворота сечения, в котором приложена эта, равен:
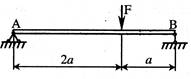
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]()
- Если балка нагружена силой F, то прогиб сечения С (vc) при EIx=const равен:
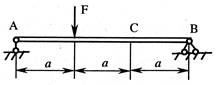
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4.
![]() .
.
- Стальная балка (модуль продольной упругости Е=2∙1011 Па) имеет длину l = 0,6 м и круговое поперечное сечение с диаметром d=60 мм. Если стрела прогиба f (наибольший прогиб) равна 2 мм, то интенсивность равномерно распределенной нагрузки q в кН/м равна:
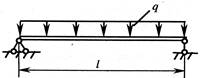
1. 150;
2. 200;
3. 250;
4. 300.
- Если на правой части консольной балки находится равномерно распределенная нагрузка интенсивности q, то угол поворота сечения В (φВ) по модулю при EIx=const равен:
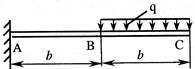
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Если балка, имеющая промежуточный шарнир С, находится под воздействием силы F, то вертикальное перемещение этого шарнира равно:
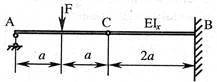
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]()
- Если однопролетная балка длиной l=2 м имеет поперечное сечение в виде двутавра (Ix=1290 см4), то под действием силы F = 50 кН угол поворота сечения над левой опорой (φА) при модуле продольной упругости E=2∙1011 Па по абсолютной величине равен:
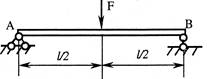
1. 0,35º;
2. 0,32º;
3. 0,28º;
4. 0,25º.
- К балке приложены два момента m. Их допускаемое значение [m] из условия жесткости [f/l]=1/400 где f – наибольший прогиб, длина l=2 м, диаметр поперечного сечения d=0,1 м и модуль продольной упругости E=2∙1011 Па, равно в кНм:
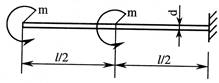
1. 21;
2. 28;
3. 35;
4. 42.
- Если половина балки находится под действием равномерно распределенной нагрузки интенсивностью q, то модуль угла поворота сечения, расположенного над левой опорой, равен:
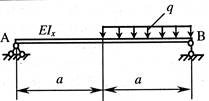
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Если сила F и прогиб под силой (vc) известны, а также заданы размер b и модуль продольной упругости Е, то осевой момент инерции поперечного сечения Ix должен быть равен:
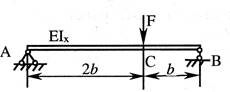
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
- Если к средней части балки приложена равномерно распределенная нагрузка интенсивности q, то максимальный прогиб f (стрела прогиба) равен:
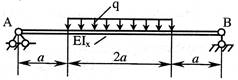
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]()
- Посередине балки приложен момент m=70кНм. Поперечное сечение – двутавр N22 (Ix=2550см4; Wx=232см3). Если модуль продольной упругости Е = 2 ∙1011Па, то абсолютная величина угла поворота сечения, расположенного над опорой (левой или правой), равна в градусах?
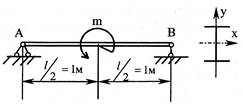
1. 0,050;
2. 0,066;
3. 0,082;
4. 0,100.
email:
KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа,
почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов