Сложное сопротивление

При простых видах деформации (осевое растяжение или сжатие, сдвиг, кручение, плоский изгиб) в поперечных сечениях возникает только одно внутреннее усилие (продольная или поперечная сила, крутящий или изгибающий момент), за исключением плоского поперечного изгиба. На практике же большинство элементов конструкций и машин подвергается действиям сил, вызывающих одновременно не одну из указанных деформаций, а две и более. Различные комбинации простых деформаций называются сложным сопротивлением.

В общем случае нагружения бруса в его поперечных сечениях действуют шесть компонентов внутренних усилий (N, Q_x, Q_y, M_x, M_y, M_кр).

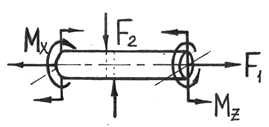
Рис.7.1

Сложный вид деформации можно рассматривать как сумму простых видов, изученных ранее (растяжение, изгиб, кручение), при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор (рис.7.2): нормальная сила N - при растяжении, изгибающий момент М_z - при чистом изгибе, крутящий момент М_x - при кручении. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми.

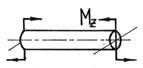
Рис.7.2

Основные соотношения, полученные для них, приведены в таблице 7.1

Таблица 7.1

Виды нагружения

Напряжения

Деформации

Растяжение

Условие прочности:

Изгиб

Условие прочности:

Кручение

Условие прочности:

Но при сложном сопротивлении должен быть применим принцип независимости действия сил (частный случай принципа суперпозиции или наложения, применяемый в механике деформируемого твердого тела).

Напомним формулировку принципа независимости действия сил: напряжение (деформация) от группы сил равно сумме напряжений (деформаций) от каждой силы в отдельности. Он справедлив, если функция и аргумент связаны линейной зависимостью. В задачах механики материалов и конструкций становится неприменимым, если:

- напряжения в какой-либо части конструкции от одной из сил или группы сил превышают предел пропорциональности ;

- деформации или перемещения становятся настолько большими, что нарушается линейная зависимость между ними и нагрузкой.

Например, дифференциальное уравнение изгиба стержня является нелинейным и вытекающая из него зависимость прогиба f от нагрузки Р для консольной балки, изображенной на рис.7.3, а, также является нелинейной (рис.7.3, б). Однако, если прогибы балки невелики (f<<l) настолько, что (так как ), то дифференциальное уравнение изгиба становится линейным (как видно из рис.7.3, б, начальный участок зависимости Р от f, описываемый этим уравнением, также является линейным).

image002-25
Рис.7.3. Модели изгиба балки: а) расчетная схема

б) линейное и нелинейное сопротивления

Задачи на сложное сопротивление решаются следующим образом. Определяются напряжения и деформации при действии простейших видов деформации, составляющих сложное сопротивление, а затем полученные результаты суммируют, используя при необходимости теории прочности.

На практике одновременное действие всех силовых факторов встречается крайне редко. Чаще приходится иметь дело с более простыми комбинациями нагружений – косой или пространственный изгиб, внецентренное растяжение или сжатие и изгиб с кручением.

Расчет балки, подверженной косому или пространственному изгибу

Косым называют изгиб, при котором плоскость действия изгибающего момента, возникающего в сечении, не совпадает ни с одной из главных плоскостей бруса (при этом плоскость действия изгибающего момента обязательно должна проходить через центр тяжести сечения) (рис.7.4).

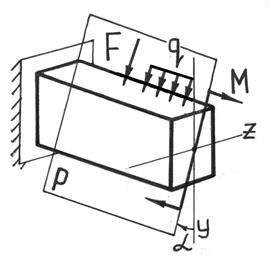
Рис.7.4

При косом изгибе изогнутая ось представляет собой плоскую кривую, и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки. При пространственном изгибе нагрузка приложена в разных плоскостях, деформированная ось является пространственной кривой.

Определение внутренних усилий при косом изгибе

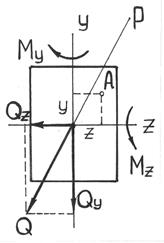
Рис.7.5

При косом изгибе в поперечных сечениях бруса действуют следующие внутренние усилия: M_z, M_y – изгибающие моменты и Q_y, Q_z –поперечные (перерезывающие) силы. Это легко показать мысленно рассекая стержень и определяя внутренние усилия при косом изгибе консольной балки под действием сосредоточенной силы F на свободном конце (см. рис.7.5):

Правило знаков для внутренних усилий: изгибающие моменты – положительны, если вызывают растяжение в положительном квадранте координатной системы zOy; поперечные силы – положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.

Таким образом, косой изгиб может быть представлен как совместное действие двух плоских изгибов в двух взаимно перпендикулярных плоскостях инерции.

Для определения полного изгибающего момента M и полной поперечной силы Q при косом изгибе достаточно определить внутренние усилия для каждого из плоских изгибов в отдельности (то есть Q_y, M_z и Q_z, M_y), а затем найти их векторную сумму:

Определение напряжений при косом изгибе

Если разложить внешние силы по главным осям инерции Ох и Оу, то получим две системы сил P_1x, P_2x, …, P_nx и P_1y, P_2y,..., P_ny, каждая из.которых вызывает прямой изгиб с изгибающими моментами соответственно M_y и М_x (рис.7.6). Применяя принцип независимости действия сил, нормальные напряжения (рис.7.7) определим как алгебраическую сумму напряжений от M_x и М_y:

Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу.

Таким образом, расчет на косой изгиб с применением принципа независимости действия сил сводится к расчету на два прямых изгиба с последующим алгебраическим суммированием напряжений.

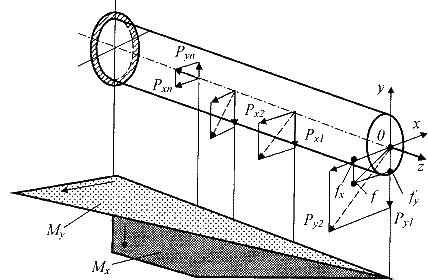
Рис.7.6. Расчетная модель косого изгиба бруса

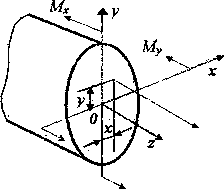
image007-24
Рис.7.7. Связь нормального напряжения с внутренними

изгибающими моментами

В случае поперечных сечений, имеющих две оси симметрии и выступающие угловые точки (рис.7.8) с равными по модулю и максимальными одноименными координатами и напряжения в этих точках будут равны

Слагаемые в этом выражении рекомендуется определять по модулю, а знаки ставить по смыслу. Например, на рис.7.9 верхний ряд знаков «+» и «—» соответствует напряжениям от М_x, а нижний ряд — от M_y, и напряжения в этих точках будут равны

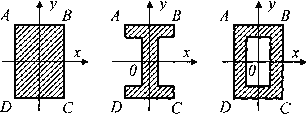
Рис.7.8. Симметричные варианты сечений

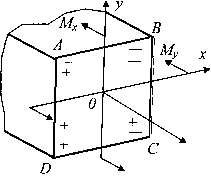
image013-24
Рис.7.9. Расстановка знаков от действия моментов

Условие прочности для балок из пластичного материала с указанным типом сечений запишется в виде

Касательные напряжения от поперечных сил, если нельзя воспользоваться формулой Журавского, допустимо не учитывать.

При проведении расчетов на прочность условие прочности составляется для опасной точки поперечного сечения, т.е. для точки, в которой нормальные напряжения достигают максимальных значений. Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии, разделяющей растянутую и сжатую зоны сечения.

В связи с этим, большое значение приобретают вопросы, связанные с определением положения нейтральной линии.

Положив , получим уравнение нейтральной линии.

Так как напряжения в точках поперечного сечения будут пропорциональными расстояниям от нейтральной линии, то будут возникать в наиболее удаленных от нее точках.

Силовая плоскость – это плоскость действия результирующего момента М_рез (рис.7.10), φ - угол наклона силовой плоскости к вертикали.

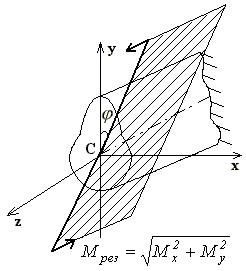
Рис.7.10

Свойства нейтральной линии

1. Если , то , то есть силовая плоскость и нейтральная линия не являются перпендикулярными.

2. Если , то из (1) следует, что , то есть нейтральная линия и силовая плоскость перпендикулярны. В этом случае стержень испытывает плоский изгиб (примерами таких стержней являются стержни с сечением – круг, кольцо, квадрат).

3. Знак «минус» в формуле (1) указывает, что силовая плоскость и нейтральная линия при косом изгибе проходят через противоположные квадранты.

Для определения опасных точек сечения следует построить касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться опасными (точки A и B на рис.7.11).

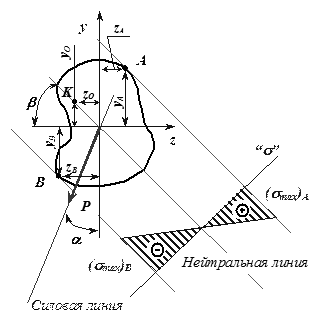
Рис.7.11. Положение нейтральной линии при косом изгибе

Для некоторых сечений (прямоугольник, двутавр, швеллер и т.п.) наиболее напряженные точки расположены в углах этих сечений, т.е. их можно найти без определения положения нейтральной линии (рис.7.12).

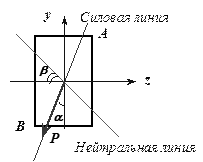
Рис.7.12. Положение нейтральной линии и опасных точек

сечения при косом изгибе для прямоугольника

Условия прочности составляют в зависимости от свойств того материала, из которого изготовлен элемент конструкции (брус).

Для хрупкого материала используют два условия прочности - для опасной точки, где имеет место растяжение (для нашего случая т.A на рис.7.11), и для точки, где имеет место сжатие (т.B)

Необходимость использования двух условий прочности для хрупкого материала объясняется разными механическими свойствами материала при растяжении и сжатии. Хрупкий материал плохо сопротивляется растяжению и хорошо - сжатию.

Для пластичного материала, который одинаково сопротивляется и растяжению и сжатию, используют одно условие прочности для точки поперечного сечения, где имеют место максимальные по абсолютной величине нормальные напряжения

где z и y - координаты данной точки.

При расчетах на прочность касательными напряжениями от поперечных сил пренебрегают, т.к. их влияние незначительно.

Определение перемещений при косом изгибе

Перемещения при косом изгибе определяют по принципу независимости действия сил, т.е. рассчитывают прогибы и в направлении главных осей, а величину полного прогиба в любом сечении балки получают геометрическим суммированием: .

Например, для балки, изображенной на рис.7.13, прогиб конца консоли определится следующим образом:

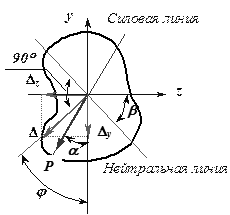
Рис.7.13. Перемещение при косом изгибе

Направление полного перемещения () определится величиной отношения (рис.7.13)

Направление полного прогиба при косом изгибе перпендикулярно нейтральной линии и не совпадает с направлением внешней силы (рис.7.13).

При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность:

1) проверка прочности;

2) подбор сечения [определить W_z (размеры сечения), при заданном отношении W_z/W_y];

3) проверка по несущей способности (определить M).

Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что и для балки, работающей при плоском поперечном изгибе. Для этого необходимо:

- построить эпюры внутренних усилий (изгибающих моментов). Для построения эпюр внутренних усилий раскладываем нагрузки на вертикальную и горизонтальную составляющие. Вертикальная составляющая вызывает изгиб относительно горизонтальной оси y, горизонтальная – относительно оси z;

- выбрать опасные сечения – это сечения, где имеет место наиболее неблагоприятное сочетание изгибающих моментов;

- в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;

- записать условие прочности в этих точках. Из условия прочности либо подобрать размеры поперечного сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной эксплуатации конструкции.

Рассмотрим примеры расчета балок на косой изгиб.

Пример 1.

Подобрать прямоугольное сечение балки (рис.7.14) при условии, что .

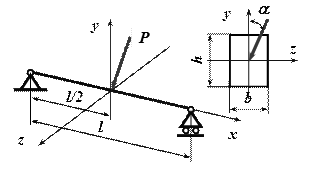
Рис.7.14

Решение:

Разложив силу P на две составляющие, действующие по направлению главных осей поперечного сечения балки, определяем опорные реакции и строим эпюры изгибающих моментов M_zи M_y (рис.7.15). Наибольшие моменты действуют в среднем сечении, где

следовательно, это сечение является опасным.

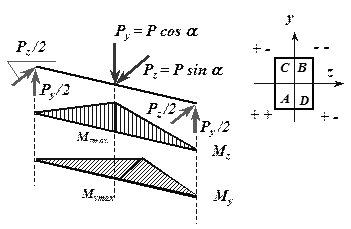
Рис.7.15. Эпюры изгибающих моментов к примеру 1

Для определения положения опасной точки расставим знаки от и в угловых точках поперечного сечения балки (рис.7.15).При действии момента в точках A и D будут иметь место положительные (растягивающие) напряжения, а в точках C и B - отрицательные (сжимающие) напряжения. При действии момента в точках A и C будут иметь место положительные , а в точках B и D - отрицательные. Точки поперечного сечения A и B, в которых действуют нормальные напряжения одного знака, являются опасными; для них и должны составляться условия прочности.

Судя по условию задачи, материал, из которого изготовлена балка, является пластичным ( =160 МПа) и, следовательно, одинаково сопротивляется деформации растяжения и деформации сжатия. Таким образом, точки A и B являются равноопасными, и для них используется одно условие прочности

Вычислим моменты сопротивления сечения при заданном соотношении высоты и ширины

Подставляя в условие прочности выражения для изгибающих моментов и моментов сопротивления, получим:

тогда h=2b=18,04 см.

Пример 2.

При установке на опоры двутавровой балки (№ 60: =182 см³, =2560 см³), предназначенной для работы на изгиб в вертикальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка и стенка двутавра отклонилась от вертикали на угол . Определить связанное с этим увеличение наибольших нормальных напряжений.

Рис.7.16. Появление внутренних изгибающих моментов

при косом изгибе к примеру 2

Решение:

Отклонение оси двутавра (ось y) от вертикали привело к возникновению косого изгиба (рис.7.16) и появлению изгибающих моментов и .

Максимальные напряжения при косом изгибе

так как , то

В случае правильной установки балки, сила P совпадала бы с вертикальной осью балки y, и имел бы место прямой изгиб, изгибающий момент был бы равен M (см. рис.7.16), а напряжения

Таким образом, максимальные напряжения при косом изгибе за счет такого незначительного отклонения от вертикали возрастут на 24,6 %.

Изгиб с растяжением (сжатием)

Если нагрузить брус в главной плоскости силой F (рис. 7.16.1,а) под углом α к оси, то в поперечном сечении 1-1 (рис. 7.16.1,б) возникнут два внутренних силовых фактора: нормальная сила N =F∙cosα и изгибающий момент M_z = F∙xsinα. Следовательно, такое нагружение бруса вызывает сочетание изгиба с растяжением (сжатием).

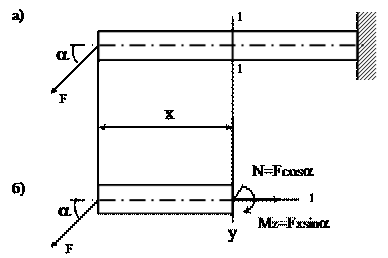
Рис.7.16.1

Считая, что брус обладает большой жесткостью при изгибе (малые величины прогиба бруса), согласно принципу независимости действия сил, можно утверждать, что в любом сечении возникают напряжения растяжения (сжатия):

и напряжения изгиба

Таким образом, суммарные напряжения в любом сечении бруса находят алгебраическим сложением напряжений σ_N и σ_MZ:

При расчетах на прочность исходят из наибольших напряжений, возникающих в любом сечении. В частности, если сечение бруса симметрично относительно нейтральной оси, то

Необходимо учитывать, что в последних двух формулах значения напряжений берутся со своими знаками плюс или минус.

Сложный изгиб (одновременный изгиб призматической балки в главных ее плоскостях)

Пример 3.

Деревянная балка прямоугольного поперечного сечения t×h (рис. 7.16.2) подвергается сложному изгибу. Требуется подобрать размеры сечения из условия прочности по нормальным напряжениям. Допускаемое напряжение [σ] = 12 МПа = 1,2 кН/см². Отношение поперечных размеров h / t = 1,5. Линейные размеры балки и нагрузка даны на рис. 7.16.3.

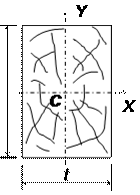
Рис.7.16.2. Поперечное сечение

Рис. 7.16.3. Исходные данные: а – заданная балка; б – расчетная схема

Решение.

1. Построение эпюр изгибающих моментов выполняется обычным образом в плоскостях X0Z и Y0Z (рис. 7.16.4).

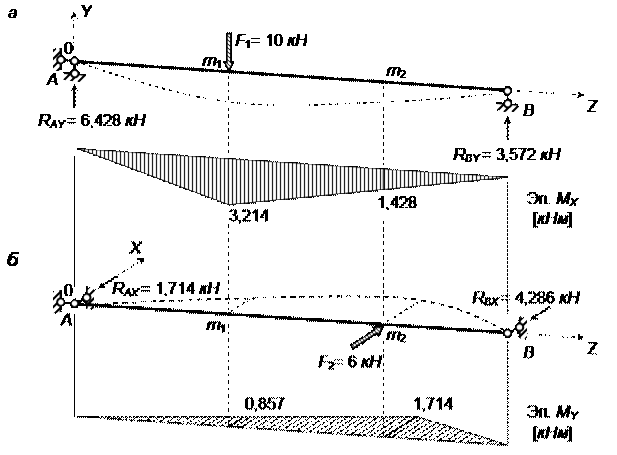
Рис. 7.16.4. Эпюры изгибающих моментов:

а – в плоскости Y0Z; б – в плоскости X0Z

2. В рассматриваемом случае условие прочности имеет вид:

где , – абсолютные величины изгибающих моментов в опасных сечениях балки; W_x, W_y – моменты сопротивления относительно главных центральных осей сечения.

Условие прочности преобразуем к виду, удобному для расчета. Моменты сопротивления вычисляются по формулам:

Вынося за скобку слагаемое и учитывая, что , получим,

откуда размер h выражается как

Опасным является сечение m₁или m₂ (рис. 7.16.4, а, б). По сечению m₁ получим

В свою очередь по сечению m₂

Имеем два результата: сечение m₁: h₁ = 15 см; t₁ = 15/1,5 = 10 см; сечение m₂: h₂ = 14,4 см; t₂ = 14,4/1,5 = 9,6 см.

Естественно принимаем больший из размеров t × h = 10 × 15 см.

Заметим, что для элементов конструкций из древесины вычисляемые размеры принято, по технологическим соображениям округлять до целых сантиметров в большую сторону. Например, пусть расчетом получены размеры h = 21,3 см, t = 12,6 см. Следует принять h = 22 см, t = 13 см.

3. Построение эпюры нормальных напряжений в опасном сечении m₁. Предварительно подсчитаем отношение осевых моментов инерции

Тогда положение нулевой линии в сечении определится как

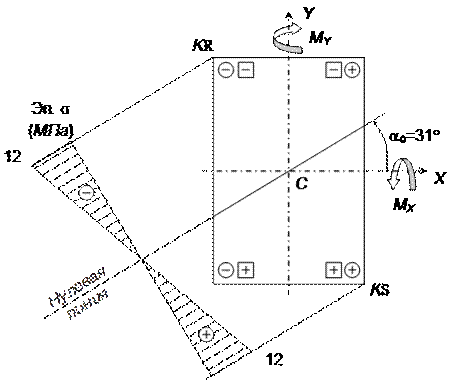
Угол наклона нулевой линии α₀≅31°. Эпюра σ дана на рис. 7.16.5.

Напряжения в опасных точках сечения

Рис. 7.16.5. Эпюра нормальных напряжений σ

и положение нулевой линии

Внецентренное сжатие или растяжение

Вторым практически важным случаем сложения деформаций от изгиба и от продольных сил является так называемое внецентренное сжатие или растяжение, вызываемое одними продольными силами. Этот вид нагружения довольно распространен в технике, так как в реальной ситуации почти невозможно приложить растягивающую нагрузку точно в центре тяжести.

Внецентренным растяжением-сжатием называется случай, когда равнодействующая сил, приложенных к отброшенной части стержня, направлена параллельно оси стержня, но не совпадает с этой осью (рис.7.17).

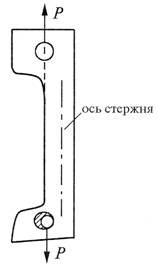
Рис.7.17

Внецентренное растяжение (сжатие) испытывают короткие стержни. Все сечения являются равноопасными, поэтому нет необходимости в построении эпюр внутренних силовых факторов.

Представим, что после проведения разреза равнодействующая Р сил действующих на отброшенную часть и приложенная к оставшейся проходит через точку с координатами (x_p; y_p) в главных центральных осях поперечного сечения (рис. 7.18).

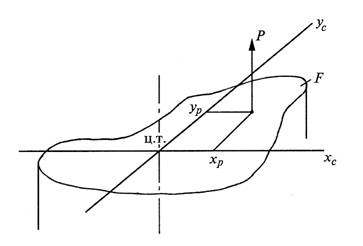
Рис.7.18

Приведем силу Р в центр тяжести сечения, т.е. направим вдоль оси стержня (сила N). При этом появятся две пары сил относительно главных центральных осей (рис.7.19).

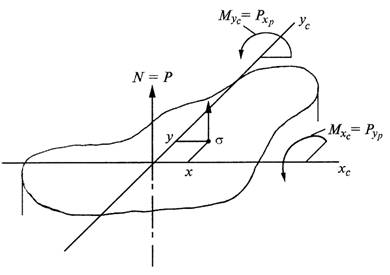
Рис.7.19

Таким образом, в поперечном сечении стержня при внецентренном растяжении и сжатии возникают три внутренних силовых фактора: нормальная сила N и два изгибающих момента относительно главных центральных осей поперечного сечения.

Для вычисления нормального напряжения в поперечном сечении в окрестности точки с произвольными координатами x,y воспользуемся принципом независимости действия сил. Будем вычислять нормальное напряжение от каждого внутреннего силового фактора в отдельности и результат сложим.

По этой формуле можно вычислять нормальные напряжения в точках поперечного сечения стержня при совместном действии осевой силы и двух изгибающих моментов. В нашем случае все три внутренних силовых фактора зависят от внецентренно приложенной силы Р (рис.7.19). Подставив соответствующие выражения в (2), получим

Вынесем величину нормального напряжения при осевом растяжении за скобки

Введем понятие о радиусе инерции относительно оси U

это такое расстояние от оси U до условной точки, где сосредоточена вся площадь сечения. Тогда момент инерции можно найти по формуле

Применив (3) в выражении , получим

Мы получили формулу нормальных напряжений в поперечном сечении при внецентренном растяжении или сжатии. Если сила растягивающая, то перед скобкой ставится знак плюс, если сила сжимающая, то ставится – минус.

В этой формуле координаты точки, где определяются напряжения входят в первой степени. Следовательно, если величины напряжений откладывать в масштабе в виде аппликат перпендикулярно плоскости поперечного сечения, то концы этих отрезков будут лежать на плоскости, наклоненной к плоскости поперечного сечения. Будем называть эту плоскость плоскостью напряжений. Известно, что две наклоненные плоскости пересекаются по линии. В нашем случае в точках этой линии - это нулевая линия, которая описывается уравнением

Анализируя (5) можно сделать вывод, что нейтральная линия при внецентренном растяжении и сжатии не проходит через центр тяжести, а отсекает на главных центральных осях отрезки и . Полагая последовательно в (5) x=0 и y=0, получим

Из формул (6) следуют некоторые закономерности, связывающие положения полюса (т. е. точки приложения силы) и нейтральной линии, которые удобно использовать для анализа решения задачи. Перечислим самые важные из этих закономерностей:

- нейтральная линия всегда расположена в квадранте, противоположном тому, в котором находится полюс (см. рис. 7.20);

- если полюс находится на одной из главных осей, то нейтральная линия перпендикулярна этой оси;

- если полюс приближается к центру тяжести сечения, то нейтральная линия удаляется от него.

- если полюс движется по прямой линии, то нейтральная линия поворачивается вокруг неподвижной точки.

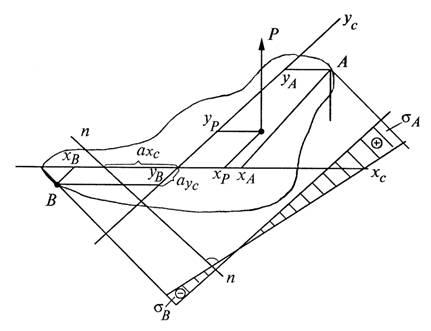
Рис.7.20

Для сечений со сложным контуром знание положения нулевой линии очень важно. Вспоминая про понятие плоскость напряжений, можно утверждать, что наибольшие по величине нормальные напряжения возникают в точках поперечного сечения наиболее удаленных от нулевой линии. Если взглянуть на плоскость напряжений вдоль нулевой линии, то она будет видна в виде линии соединяющей аппликаты напряжений, то есть в виде эпюры напряжений, отложенной от линии перпендикулярной нулевой линии (рис.7.20).

Наибольшее растягивающее нормальное напряжение возникает в точке А

а наибольшее сжимающее нормальное напряжение возникает в точке В

Таким образом, при внецентренном растяжении кроме растягивающих нормальных напряжений в поперечном сечении могут возникнуть и сжимающие. При внецентренном сжатии – наоборот.

Если материал стержня одинаково сопротивляется растяжению и сжатию, то условие прочности получает такой вид:

Хрупкий материал обладает различными свойствами в условиях растяжения и сжатия – плохо сопротивляется растяжению и хорошо сжатию, условия прочности составляют для двух точек: где действуют максимальные растягивающие (т. A) и максимальные сжимающие (т. B) напряжения

Для поперечных сечений с выступающими углами, у которых обе главные оси инерции являются осями симметрии (прямоугольник, двутавр и др.) и . Поэтому формула упрощается, и мы имеем

Если же материал стержня неодинаково сопротивляется растяжению и сжатию, то необходимо проверить прочность стержня как в растянутой, так и в сжатой зонах.

Пример 4.

Чугунный короткий стержень, поперечное сечение которого изображено на рис. 7.21, а = 3 cм, b = 2 см, сжимается продольной силой Р, приложенной в точке А. Допускаемые нормальные напряжения: на сжатие ; на растяжение МПа.

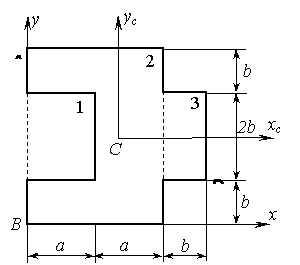
Рис.7.21

Требуется:

1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив величины этих напряжений через Р и размеры сечения;

2) найти допускаемую нагрузку (Р) при заданных размерах сечения и допускаемых напряжениях чугуна на сжатие и на растяжение .

Решение.

Нормальное напряжение в произвольной точке сечения стержня, определяемой координатами х и у, запишется в виде

где х_р, у_р - координаты точки приложения силы Р (точки A); F -площадь поперечного сечения стержня; J_xc, J_yc - главные моменты инерции сечения.

1. Определим координаты центра тяжести сечения х_с и у_с. Для этого выведем вспомогательную систему координат хоу. Тогда , где - статический момент сечения: . Индексы 1, 2, 3 относятся соответственно к элементарным фигурам, на которые разбито заданное составное сечение (см. рис. 7.22). Отметим также, что площадь первой фигуры следует брать со знаком минус.

Рис. 7.22

Подставляя исходные данные, получим:

Тогда

Ввиду симметрии сечения у = 2b = 4 см. Через найденный центр тяжести проводим главные центральные оси х_с и у_с.

2. Вычислим главные моменты инерции.

Ввиду совпадения осей х_с и х_с₁, х_с₂, х_с₃:

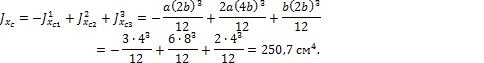
Для вычисления момента инерции относительно оси у_с используем формулу изменения момента инерции при параллельном переносе осей:

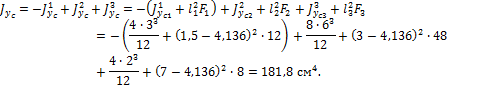
Здесь через l₁, l₂, l₃ обозначены^: соответственно расстояния между осью у_с и осями у_с₁, у_с₂, у_с₃.

3. Нахождение наибольших напряжений и допускаемых нагрузок.

Подставляя в формулу (10) вычисленные значения моментов инерции, а также координаты точки приложения нагрузки и точек, где возникают наибольшие растягивающие и сжимающие напряжения, получим:

В точке А(-4,136; 4) - напряжение сжатия

Из условия прочности при сжатии

множитель 10⁴ здесь переводит квадратные, сантиметры в метры. Допускаемая нагрузка

В точке D (3,864;-2) возникает максимальное напряжение растяжения

Из условия прочности при растяжении

Допускаемая нагрузка

Выбирая меньшую из двух нагрузок, окончательно принимаем

В ходе решения этой задачи можно также порекомендовать построение нейтральной оси в случаях, когда трудно сразу определить координаты опасных точек. Для определения положения опасных точек в сечении следует параллельно нейтральной оси провести линии, касающиеся контура сечения. Таким образом, будут найдены точки сечения, расположенные по oбe стороны от нейтральной оси и наиболее удаленные от нeё, которые и являются опасными.

Пример 5.

Стальная полоса шириной H=10 см и толщиной t=1 см, центрально растянутая силами P=70 кН, имеет прорезь шириной h=3 см (рис. 7.23). Определить наибольшие нормальные напряжения в сечении AB, не учитывая концентрации напряжений. Какой ширины h могла бы быть прорезь при той же величине растягивающего усилия, если бы она была расположена посередине ширины полосы?

Рис.7.23

Решение.

При несимметричной прорези центр тяжести ослабленного сечения смещается от линии действия силы вправо и возникает внецентренное растяжение. Для определения положения центра тяжести () ослабленное сечение представим как большой прямоугольник размерами (фигура I) из которого удален малый прямоугольник с размерами (фигура II). За исходную ось примем ось x.

В этом случае в поперечном сечении AB возникает два внутренних силовых фактора: продольная сила N=P и изгибающий момент

С целью определения опасной точки расставим знаки напряжений по боковым сторонам поперечного сечения (рис. 7.23). От продольной силы во всех точках сечения имеют место положительные (растягивающие) напряжения. От изгибающего момента слева от оси имеют место растягивающие напряжения (знак плюс), справа – сжимающие (знак минус).

Таким образом, максимальные нормальные напряжения возникают в т.A

где - площадь ослабленного сечения, равная 7 см²;

- момент инерции ослабленного сечения относительно главной центральной оси .

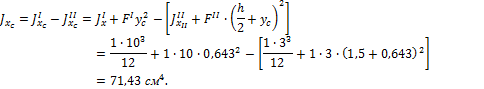
- расстояние от нейтральной линии () до наиболее удаленной точки (т. A)

см.

В результате максимальные нормальные напряжения будут равны

При симметричной прорези шириной h₁ возникает только растяжение

тогда

Ядро сечения при внецентренном сжатии

При конструировании стержней из материалов, плохо сопротивляющихся растяжению (бетон), весьма желательно добиться того, чтобы все сечение работало лишь на сжатие. Этого можно достигнуть, не давая точке приложения силы Р слишком далеко отходить от центра тяжести сечения, ограничивая величину эксцентриситета.

Конструктору желательно заранее знать, какой эксцентриситет при выбранном типе сечения можно допустить, не рискуя вызвать в сечениях стержня напряжений разных знаков. Здесь вводится понятие о так называемом ядре сечения. Этим термином обозначается некоторая область вокруг центра тяжести сечения, внутри которой можно располагать точку приложения силы Р, не вызывая в сечении напряжений разного знака.

Рис. 7.24 поясняет данное определение ядра сечения.

Рис.7.24

При приложении силы Р в точке на границе ядра сечения с координатами (x_я; y_я) нулевая линия будет касательной к контуру поперечного сечения в точке В (рис.7.25) и отсекать на главных центральных осях отрезки и .

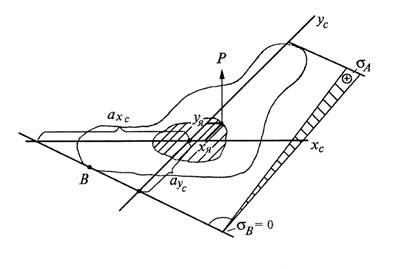
Рис. 7.25

Применяя (6), получим

Формулы (11) описывают алгоритм вычисления координат точек границы ядра сечения:

1) Проводится касательная к контуру поперечного сечения и определяются отрезки и .

2) По формуле (11) определяются координаты x_я и y_я.

Такая процедура проводится со всеми касательными. Для сложного криволинейного контура, чем больше будет проведено касательных, тем точнее будет найден контур ядра сечения.

Можно доказать, что если касательная будет вращаться вокруг угла контура сечения, если он есть, то соответствующая точка на контуре ядра будет перемещаться по прямой линии, соединяющей точки ядра соответствующие крайним положениям касательных.

Таким образом, если контур поперечного сечения представляет собой многоугольник, что контур ядра сечения тоже будет иметь форму многоугольника, но необязательно с тем же количеством углов (их может быть меньше).

Для прямоугольного сечения ядро будет ромбом с диагоналями, равными одной трети соответствующей стороны сечения. Поэтому прямоугольное сечение при расположении силы по главной оси работает на напряжения одного знака, если точка приложения силы не выходит за пределы средней трети стороны сечения.

Для круглого сечения радиуса r очертание ядра будет по симметрии кругом радиуса . Возьмем какое-либо положение нейтральной оси, касательное к контуру. Ось Оу расположим перпендикулярно к этой касательной. Тогда

Таким образом, ядро представляет собой круг с радиусом, вчетверо меньшим, чем радиус сечения.

Для двутавра нейтральная ось при обходе контура не будет пересекать площади поперечного сечения, если будет касаться прямоугольного контура ABCD, описанного около двутавра (рис.7.26, а). Следовательно, очертание ядра для двутавра имеет форму ромба, как и для прямоугольника, но с другими размерами.

Для швеллера, как и для двутавра, точки 1, 2, 3, 4 контура ядра (рис.7.26, б) соответствуют совпадению нейтральной оси со сторонами прямоугольника ABCD.

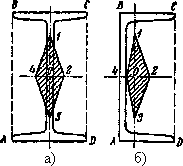
image037-17
Рис.7.26. Ядро сечения для двутавра — а) и швеллера — б)

Пример 6.

Для бруса определить грузоподъемность [F] при К₁= 0,5; К₂= 2; [σ]= 20 МПа = 2 кН/см² из условия прочности по нормальным напряжениям. Схема поперечного сечения показана на рис. 7.26.1. Схема бруса и нагрузки дана на рис.7.26.2.

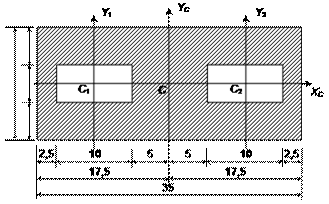
Рис.7.26.1. Поперечное сечение (размеры указаны в сантиметрах)

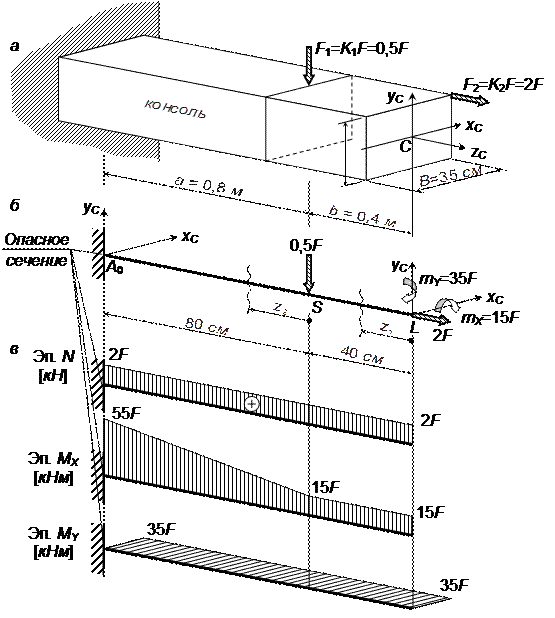
Рис. 7.26.2. Сложное сопротивление жесткого бруса:

а – заданная система; б – приведение сил к главным осям;

в – эпюры внутренних усилий

Решение.

1. Геометрические характеристики сечения.

В силу симметрии сечения оси x_CСy_C – главные.

Площадь A=35∙15 - 2∙10∙5=425 см².

Главные центральные моменты инерции:

Моменты сопротивления:

Радиусы инерции:

Квадраты радиусов инерции:

2. Приведение внешних сил к главным осям торцового сечения консоли (рис.7.26.3).

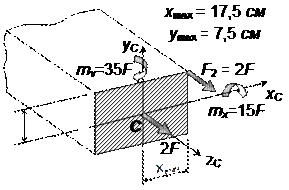
Рис.7.26.3. Приведение нагрузки к главным осям торцевого сечения

Перенося силу F₂=2F к центру С сечения, получаем эквивалентную систему нагрузок на торце консоли, включающую силу 2F и моменты относительно осей x_C и y_C:

3. Построение эпюр усилий (рис. 7.26.2, в).

Участок SL.

N=2F=const – растяжение;

M_x=m_x=15F кНсм=const – растянуты верхние волокна;

M_y=m_y=35F кНсм=const – растянуты правые волокна.

Участок А₀S.

N=2F=const – растяжение;

M_x=m_x+F₁z₂=15F +0,5F∙z₂ – растянуты верхние волокна;

M_x(0)=15F кНсм;

M_x(80)=15F +0,5F∙80 =55F кНсм;

M_y=m_y=35F кНсм=const – растянуты правые волокна.

4. Условие прочности для опасной точки опасного сечения A₀.

В угловых точках показаны знаки нормальных напряжений от N (£), MX (), MY (r). Опасной является точка f (рис. 7.26.4).

Рис.7.26.4. Определение опасной точки в опасном сечении

Условие прочности для опасной точки f имеет вид

При подстановке в условие прочности внутренних усилий в опасном сечении N = 2F, M_x = 55F, M_y = 35F получим

Итак, допускаемая грузоподъемность соответствует нагрузке F₁ = 0,5F = 16,15 кН, F₂ = 2F = 64,6 кН.

5. Построение ядра сечения (рис. 7.26.5).

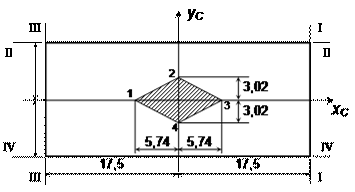
Рис.7.26.5. Ядро сечения (размеры указаны в сантиметрах)

Координаты угловых точек ядра в осях x_CСy_C вычисляются по формулам:

где a_X, a_Y – отрезки, отсекаемые на главных осях касательными к контуру сечения нулевыми линиями I, II, III, IV, откуда получим координаты точек 1, 2, 3, 4. Например, задав нулевую линию I–I, имеем a_X = +17,5 см, a_Y = ∞, так что координаты точки 1 и т. д.

Координаты точек:

т.2 (x₂ = 0; y₂ = +3,02 см);

т.3 (x₃ = +5,74 см; y₃ = 0);

т.4 (x₄ = 0; y₄ = –3,02 см).

Критерии предельного состояния материала при сложном напряженном состоянии. Теории прочности

Для определения напряженного состояния в какой-нибудь точке тела, нужно вокруг этой точки выделить элементарный параллелепипед. По граням этого параллелепипеда, в общем случае, будут действовать нормальные и касательные, напряжения. Зная эти напряжения, всегда можно найти главные напряжения и главные площадки. Следовательно, напряженное состояние в каждой точке тела, в конечном счете, будет определяться тремя главными напряжениями σ₁, σ₂, σ₃. Если из трех главных напряжений два равны нулю, то будет иметь место линейное напряженное состояние в данной точке тела. Если из трех главных напряжений только одно равно нулю, то будет иметь место плоское напряженное состояние в данной точке тела. Если ни одно из главных напряжений не равно нулю, то будет иметь место объемное напряженное состояние в данной точке тела. Если во всех точках тела будет один и тот же тип напряженного состояния, то будет иметь место однородное напряженное состояние тела. Линейное напряженное состояние называют простым напряженным состоянием, плоское и объемное напряженное состояние - сложным. Тип напряженного состояния нельзя отождествлять с одноименным видом деформации; так при линейном напряженном состоянии могут происходить объемные деформации и т. д.

Гипотезы (теории) прочности

Установлено, что в каждой точке нагруженного тела, в общем случае действует три главных напряжения.

Опыт показывает, что поведение материалов, т.е. начало стадии пластических деформаций и характер разрушения (хрупкий, вязкий), зависят от величины, знака и соотношения главных напряжений.

Поэтому, чтобы судить о прочности материала при сложном напряженном состоянии, нужно предварительно знать - в какой момент при той или иной комбинации главных напряжений наступает опасное состояние материала.

При простом напряженном состоянии ответ на этот вопрос дают диаграммы растяжения или сжатия. Предельными напряжениями считаются такие, при которых хрупкий материал разрушается, а пластичный материал получает недопустимо большие пластические деформации.

При сложном напряженном состоянии решение этой задачи значительно сложнее, т. к. число различных сочетаний из главных напряжений неограниченно велико, а опыт технически очень сложен.

Вследствие этого при составлении условий прочности материала при сложном напряженном состоянии мы можем располагать только допускаемыми напряжениями, установленными по результатам испытаний на простое растяжение или сжатие.

В связи с этим возникает задача: зная максимально допустимые безопасные напряжения при простом растяжении, найти эквивалентную, т. е. равно безопасную комбинацию из главных напряжений при сложном напряженном состоянии.

Единственным практическим путем решения этой задачи является установление общих критериев разрушения, которые позволили бы оценить опасность перехода материала в предельное состояние при сложном напряженном состоянии, используя лишь данные опытов на растяжение.

Критерии разрушения или гипотезы прочности представляют собой предположения о преимущественном влиянии на прочность материалов того или иного фактора, сопутствующего процессу деформации и разрушения материалов.

Наиболее важными факторами, связанными с возникновением опасного состояния материала, являются: нормальные и касательные напряжения, линейные деформации и потенциальная энергия деформации.

Который из этих факторов является главной причиной разрушения установить не удается, т.к. невозможно наблюдать действие какого-нибудь одного фактора изолированно от остальных.

При сложном напряженном состоянии следует говорить не о предельном напряжении, а о предельном напряженном состоянии. В качестве предельного состояния в опасной точке детали принимается переход материала в окрестности данной точки из упругого состояния в пластическое или разрушение детали, выражающееся в образовании трещин.

Условимся рассматривать такие случаи напряженного состояния, когда все нагрузки возрастают пропорционально некоторому параметру, вплоть до наступления предельного напряженного состояния. При этом главные напряжения также возрастают пропорционально.

Коэффициентом запаса прочности при сложном напряженном состоянии называется число, на которое следует умножить все компоненты тензора напряжений (или s₁, s₂, s₃), чтобы данное напряженное состояние стало предельным.

Равноопасными называются такие напряженные состояния, для которых коэффициенты запаса прочности равны.

Это дает возможность сравнивать все напряженные состояния между собой, заменяя их равноопасным одноосным напряженным состоянием (растяжением).

Эквивалентным напряжением называется напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние стало равноопасным заданному напряженному состоянию (рис.7.27).

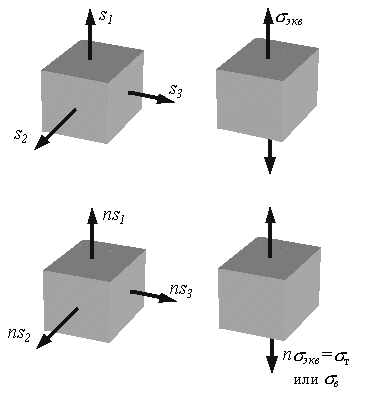
Рис. 7.27

Заменяя сложное напряженное состояние эквивалентным растяжением, получаем возможность использовать при сложном напряженном состоянии условие прочности при простом растяжении:

Условие наступления предельного состояния имеет следующий вид:

или

Теория наибольших нормальных напряжений (I теория прочности, Галилей, 1638 г.)

В основу теории наибольших нормальных напряжений положена гипотеза о преимущественном влиянии наибольших по абсолютной величине нормальных напряжений.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из главных напряжений достигает величины, соответствующей пределу прочности при простом растяжении.

В этом случае условие прочности должно иметь вид:

- при растяжении, (14)

- при сжатии. (15)

Данная гипотеза удовлетворительно согласуется с результатами испытания деталей из хрупких материалов, таких как камень, кирпич, чугун. Для расчета деталей из пластичных материалов данная гипотеза непригодна.

Теория наибольших линейных деформаций (II теория прочности, Мариотт, 1682 г.)

В основу теории наибольших линейных деформаций положена гипотеза о преимущественном влиянии наибольших по абсолютной величине линейных деформаций.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из относительных удлинений достигает опасной величины, соответствующей пределу прочности при простом растяжении.

Максимальные относительные деформации в соответствии с обобщенным законом Гука.

- при растяжении, (16)

- при сжатии. (17)

При простом растяжении

Предельное значение относительной деформации при растяжении

На основании сформулированной гипотезы, имеем

или с учетом (16), (19)

Сравнивая с условием наступления предельного состояния (13), получим эквивалентное напряжение по II теории прочности:

Условие прочности в соответствии с (12) имеет следующий вид:

- при растяжении, (23)

- при сжатии. (24)

Из (19), (20) вытекает, что простое растяжение более опасно нежели сложное. Опыты этого не подтверждают. В связи с этим данная теория для расчета деталей не используется.

Теория наибольших касательных напряжений (III теория прочности; Кулон, 1773 год)

В основу теории наибольших касательных напряжений положена гипотеза о преимущественном влиянии наибольших по абсолютной величине касательных напряжений.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из касательных напряжений достигает величины, соответствующей пределу текучести при простом растяжении.

При объемном напряженном состоянии:

При простом растяжении (s₂=s₃=0)

Предельное значение максимальных касательных напряжений при растяжении

На основании сформулированной гипотезы, имеем

или с учетом (25), (26)

Сравнивая с условием наступления предельного состояния (13), получим эквивалентное напряжение по III теории прочности:

Условие прочности в соответствии с (12) имеет следующий вид:

Для плоского напряженного состояния условие (31) примет вид

На практике встречаются случаи, когда σ_y =0, тогда

Условие прочности (31) хорошо согласуется с результатами испытания изотропных материалов, поэтому данная теория широко применяется для расчета деталей из металлических материалов.

Теория наибольшей удельной потенциальной энергии формоизменения (IV теория прочности; Бельтрами - 1885 г.; Губер - 1904 г.)

В основу энергетической теории прочности положена гипотеза о преимущественном влиянии удельной потенциальной энергии изменения формы.

Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда удельная потенциальная энергия изменения формы достигает величины, соответствующей пределу текучести при простом растяжении.

При объемном напряженном состоянии удельная потенциальная энергия изменения формы, выраженная через главные напряжения, определяется следующим уравнением:

При простом растяжении (s₂=s₃=0)

Предельное значение удельной потенциальной энергии изменения формы при растяжении

На основании сформулированной гипотезы, имеем

или с учетом (32) и (34)

Сравнивая с условием наступления предельного состояния (13), получим эквивалентное напряжение по IV теории прочности:

Условие прочности в соответствии с (12) имеет следующий вид:

Для плоского напряженного состояния соотношение (37) принимает вид

В частном случае, когда σ_y = 0, то, приняв σ_x = σ и τ_xy = τ, найдем

Рассмотренная теория хорошо согласуется с экспериментами для пластичных материалов и широко применяется на практике.

Теория прочности Мора (V теория прочности)

Теория прочности Мора позволяет учесть различие в свойствах материалов при растяжении и сжатии. Ее можно получить путем модификации теории наибольших касательных напряжений в соответствии с уравнением:

При одноосном сжатии в предельном случае s₁=0,

откуда определяется коэффициент k

для пластичных материалов, или

для хрупких материалов.

Условие прочности по теории Мора имеет следующий вид:

Замечания о выборе теории прочности

Обзор многочисленных теорий предельных состояний показывает, что совершенных теорий еще нет. Каждая из существующих теорий справедлива только в определенных условиях и для определенных материалов. Рассмотренными выше теориями можно пользоваться только при напряженных состояниях с главными напряжениями разных знаков. Возможность применения этих теорий в случаях трехосного растяжения или сжатия требует дополнительной экспериментальной проверки.

При выборе теории прочности в случае плоского напряженного состояния и объемного напряженного состояния с главными напряжениями разных знаков надо учитывать свойства материала. Если материал пластичен и одинаково работает на растяжение и сжатие, то следует пользоваться теорией наибольшей энергии формоизменения или теорией максимальных касательных напряжений. Если пластичный материал неодинаково сопротивляется растяжению и сжатию, то следует применить теорию Мора. Расчет хрупких материалов при указанных напряженных состояниях следует производить по теории Мора.

Пример 7.

Определить допускаемое касательное напряжение, используя III и IV теории прочности.

Как известно при чистом сдвиге s₁=, s₃=, s₂=0.

Эквивалентное напряжение по теории максимальных касательных напряжений при чистом сдвиге имеет следующий вид:

откуда получаем

Эквивалентное напряжение по теории удельной потенциальной энергии формоизменения при чистом сдвиге имеет следующий вид:

откуда получаем

Оба результата неплохо согласуются с опытными данными

Пример 8.

Проверить прочность вала, передающего крутящий момент 1000 Нм по теории максимальных касательных напряжений, если диаметр вала d=4 см, основное допускаемое напряжение =160 МПа.

Максимальное касательное напряжение при кручении круглого вала

При кручении в поперечных сечениях имеет место напряженное состояние чистого сдвига s₁=, s₃=, s₂=0. Условие прочности по теории максимальных касательных напряжений имеет следующий вид:

Условие прочности удовлетворяется.

Пример 9.

Подобрать диаметр вала, передающего крутящий момент 1000 Нм на основании теории прочности Мора, если =400 МПа, =1600 МПа, коэффициент запаса прочности при растяжении n=4.

Коэффициент k условия прочности Мора (43) определяется по уравнению (42)

Допускаемое напряжение на растяжение определяется из следующего уравнения

Условие прочности по теории Мора при чистом сдвиге, имеющем место при кручении, имеет следующий вид:

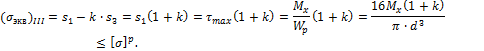
Откуда определяется потребный диаметр вала

Пример 10.

Определить аналитические выражения эквивалентных напряжений по III и IV теориям прочности для напряженного состояния, имеющего место в промежуточных точках поперечного сечения при плоском прямом поперечном изгибе бруса.

Главные напряжения в промежуточных точках поперечного сечения при плоском прямом поперечном изгибе бруса определяются уравнением

Следовательно, эквивалентное напряжение по III теории прочности в этом случае имеет следующий вид:

Эквивалентное напряжение по IV теории прочности имеет следующий вид:

С помощью данных уравнений можно проводить полную проверку прочности балок с учетом как нормальных, так и касательных напряжений, действующих в поперечных сечениях.

Пример 11.

Определим запас прочности по пластическим деформациям болта соединения (рис.7.27.1) с резьбой М24x1,5, если в результате затяжки в нем создано усилие F₀ = 45 кН, а момент сопротивления резьбе (крутящий момент) составлял Т_з = 200 Н∙м. Материал болта – углеродистая сталь (σ_Т = 650 МПа).

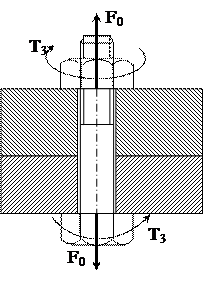
Рис.7.27.1

Решение.

Оценим сначала прочность болта в сечении минимального диаметра по впадинам резьбы. По стандарту находим, что внутренний диаметр резьбы d₁ = 22,38 мм.

Определим напряжение растяжения в болте от усилия затяжки:

Вычисляем теперь касательные напряжения от момента в резьбе (обусловлен трением витков и подъемом витков).

Теперь находим эквивалентное напряжение по IV теории прочности

Определяем запас прочности

Совместные действия изгиба и кручения стержня

На практике деформации кручения часто сопутствует изгиб. Как правило, при работе вал изгибается собственным весом, весом шкивов, давлением на зубья шестерен, натяжением ремней и т.д. Сочетание изгиба с кручением имеет место в пространственных рамах, коленчатых валах и других элементах конструкций.

В предыдущих разделах рассматривались такие частные случаи сложного сопротивления (косой изгиб, внецентренное растяжение или сжатие), при которых в поперечных сечениях бруса возникали только нормальные напряжения, и, следовательно, имело место одноосное напряженное состояние. Это позволило при выводе расчетных формул использовать сечения произвольной формы.

В случае изгиба с кручением от крутящего момента в поперечных сечениях бруса возникают касательные напряжения, которые рассчитываются по разному для круглых и прямоугольных брусьев. Вследствие этого, рассматривать расчет сечений произвольной формы не представляется возможным.

Кручение с изгибом – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.

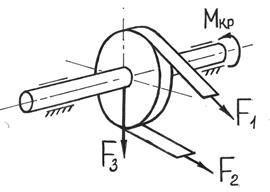
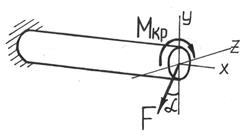
Рис.7.28

Определение внутренних усилий и напряжений при кручении с изгибом

Для определения внутренних усилий воспользуемся методом сечений:

Обычно две составляющие поперечной силы (Q_y, Q_z) и изгибающего момента (M_y, M_z) приводят к их полным результирующим

Заметим, что часто поперечной силой пренебрегают (для достаточно длинных валов) и рассматривают кручение с изгибом как совместное действие крутящего (M_x, M_кр, T) и изгибающего (M_и) моментов.

Расчет валов круглого (кольцевого) поперечного сечения на кручение с изгибом

Исследуем этот вид деформации стержня на примере расчета вала кругового (кольцевого) поперечного сечения на совместное действие изгиба и кручения (рис. 7.29).

Рис.7.29

Примем следующий порядок расчета.

1. Разлагаем все внешние силы на составляющие P_1x, P_2x,..., P_nx и P_1y, P_2y,..., P_ny.

2. Строим эпюры изгибающих моментов M_ч и M_y. от этих групп сил.

У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента M_x, и M_y, а целесообразно их заменить результирующим (суммарным) изгибающим моментом (рис.7.30)

который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси п—п, перпендикулярной вектору М_изг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру М_изг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.

image003-27
Рис.7.30

3. Строится эпюра крутящего момента М_z.. Эпюра крутящих моментов строится так же, как и при чистом кручении.

4. Находится опасное сечение вала.

Опасное сечение вала будем искать, как и прежде, по эпюрам внутренних усилий. При построении эпюр внутренних усилий при кручении с изгибом необходимо иметь ввиду следующие правила:

- эпюры крутящего момента M_x, а также эпюры составляющих поперечной силы Q_y, Q_z и изгибающего момента M_y, M_z строятся по той же процедуре, что и ранее;

- результирующая поперечная сила Q может не лежать в плоскости действия результирующего изгибающего момента M_и, а потому между ними уже не будет соблюдаться зависимость Журавского (dM/dx=Q), а, следовательно, и правила проверки эпюр, введенные для плоского изгиба;

- эпюра полного изгибающего момента будет прямой только на тех участках, где M_y и M_z ограничены прямыми с общей нулевой точкой, на участках, где такая общая точка отсутствует эпюра M_и будет описываться вогнутой кривой и строится по точкам (связано с тем, что вектор M_и в разных сечениях имеет различное направление).

Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего M_x и полного изгибающего M_и моментов. Если в сечении вала постоянного диаметра с наибольшим изгибающим моментом М действует наибольший крутящий момент М_кр, то это сечение является опасным.

Если же такого явного совпадения нет, то опасным может оказаться сечение, в котором ни М ни М_кр не являются наибольшими. Еще больше осложняется задача при валах переменного диаметра; у таких валов наиболее опасным может оказаться такое сечение, в котором действуют значительно меньшие изгибающие и крутящие моменты, чем в других сечениях.

В случаях, когда опасное сечение не может быть установлено непосредственно по эпюрам М и М_кр , необходимо проверить прочность вала в нескольких предположительно опасных сечениях.

5. После установления опасного сечения вала в нем находят опасные точки. В сечении возникают одновременно нормальные напряжения от изгибающего момента и касательные напряжения от крутящего момента и поперечной силы. В валах круглого сечения, длина которых во много раз больше диаметра, величины наибольших касательных напряжений от поперечной силы относительно невелики и при расчете прочности валов на совместное действие изгиба и кручения не учитываются.

Наибольшие напряжения изгиба возникают в точках k и k^/, наиболее удаленных от нейтральной оси (рис. 7.31),

где W_изг — момент сопротивления при изгибе.

В этих же точках имеют место и наибольшие касательные напряжения кручения

где W_р— момент сопротивления при кручении.

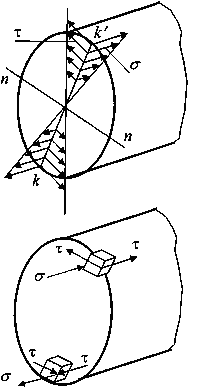
Рис.7.31

Как видно из рис. 7.31, в данном случае имеет место плоское напряженное состояние и расчет на прочность должен вестись по одной из гипотез прочности. Для пластичных материалов применяют гипотезу наибольших касательных напряжений (III) или энергетическую гипотезу (IV).

Условие прочности по III гипотезе записывается в виде

В рассматриваемом случае

или

где - эквивалентный момент по третьей гипотезе прочности.

Условие прочности по IV гипотезе прочности записывается в виде

В рассматриваемом случае

или

где - эквивалентный момент по четвертой гипотезе прочности.

Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к третьей гипотезе, а для очень хрупких – к первой гипотезе

Аналогичный расчет проводится и для кольцевого сечения.

Пример 12.

Стальной вал круглого поперечного сечения передает мощность N=14,7 кВт при угловой скорости =10,5 рад/с. Величина наибольшего изгибающего момента, действующего на вал M_и=1,5 кНм. Исходя из условий прочности по III и IV теориям прочности, определить необходимый диаметр вала, если =80 МПа.

Решение.

Условие прочности при одновременном действии изгиба и кручения по III гипотезе прочности

Находим величину передаваемого валом крутящего момента

Эквивалентный момент по третьей гипотезе прочности равен

а диаметр вала

или =63,5 мм.

Условие прочности при одновременном действии изгиба и кручения по IV гипотезе прочности

Эквивалентный момент по четвертой гипотезе прочности равен

а диаметр вала

или =62,3 мм.

Таким образом, расчет по энергетической теории прочности дал более экономичный размер сечения, чем по критерию наибольших касательных напряжений.

Пример 13.

Рассмотрим вал, нагруженный так, как это показано на рис. 7.31.1,а. Вал передает от левого конца к зубчатому колесу, диаметром d = 1/3 м, мощность P = 15 кВт при частоте вращения n = 382 об/мин. Следует из условия прочности рассчитать необходимый диаметр вала. Принять [σ] = 80 МПа.

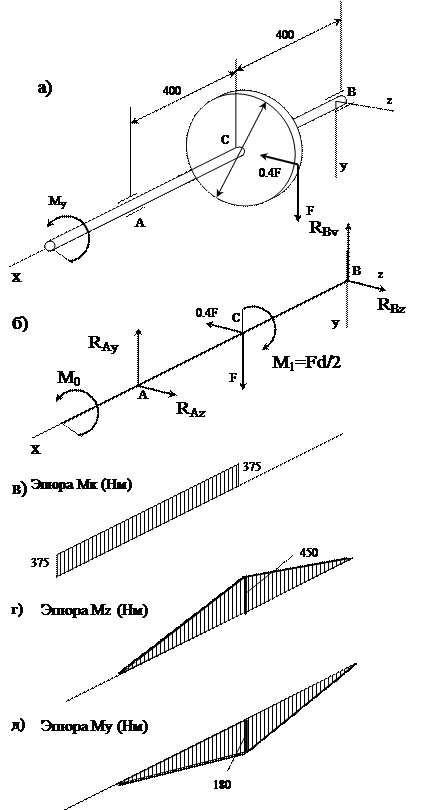
Рис.7.31.1

Решение.

1. Для решения этой задачи необходимо в первую очередь составить расчетную схему вала. Приведем силу F к точке С на оси вала. Для этого заменим силу F системой сил ей эквивалентной: силой F, приложенной к оси вала, и парой сил с моментом M₁ = F(d/2), действующим в плоскости зубчатого колеса. Далее освободим вал в точках А и В от опор (подшипников), заменив их реакциями в горизонтальной () и вертикальной () плоскостях. В результате получаем расчетную схему вала (рис. 7.31.1, б).

2. Исходя из того, что вал передает мощность P = 15 кВт при частоте вращения n соответствующей угловой скорости ω = πn/30, находим вращательный момент M₀, приложенный к левому концу вала:

Из равенства M₀ = M₁ = Fd/2 находим касательную силу F:

Следовательно, радиальная сила 0,4F = 900 H.

3. Находим реакции опор, воспользовавшись симметричным их расположением относительно зубчатого колеса

4. Осуществляем построение эпюр моментов в трех взаимно перпендикулярных плоскостях: YOZ, XOY, XOZ. На участке от левого конца до зубчатого колеса вал скручивается моментами M₀ и M₁. Следовательно, в любом сечении на этом участке крутящий момент M_к= |M₀| = |M₁| = 375 H∙м. Следовательно, эпюра M_к имеет вид прямой (const), показанной на рис. 7.31.1,в.

В плоскости XOY под действием сил вал изгибается на участке между опорами А и В. В сечениях, проходящих через эти точки, изгибающие моменты равны нулю, а наибольшего значения изгибающий момент M_z (вращение момент осуществляет относительно оси OZ) достигает в сечении, совпадающим со средней плоскостью зубчатого колеса

Эпюра M_z изображена на рис. 7.31.1,г.

В плоскости XOZ вал изгибается на том же участке под действием сил .

Наибольший изгибающий момент (рис. 7.31.1,д) имеет место в том же сечении, что и M_z_max:

5. Рассчитываем эквивалентный момент, используя третью гипотезу прочности, в опасном сечении вала, проходящего через точку С:

6. Из условия прочности (45), полагая σ_э = [σ], находим требуемый момент сопротивления сечения вала:

По значению W_и определяем диаметр вала по формуле:

Пример 14.

Для конструкции (рис. 7.31.2), у которой участок A₀–B круглого сечения, проверить прочность в опасной точке участка A₀–B при [σ]= 160 МПа = 16 кН/см².

Рис.7.31.2. К примеру 12: а – заданная схема, б –расчетная схема,

в – эпюры внутренних усилий

Решение.

1. Построение эпюр усилий на участке A₀–B. По рис. 7.31.1, б имеем следующее.

Участок S–B: 0≤ z₁ ≤0,5 м;

Участок A₀–S: 0≤ z₂ ≤0,3 м;

В рассматриваемом случае влиянием поперечных сил Q_x и Q_y пренебрегаем из-за их малой величины, поэтому эпюры Q_x и Q_y не приводятся.

2. Установление опасной точки в опасном сечении.

Опасным сечением участка A₀–B является сечение A₀ (защемление), так как в этом сечении все усилия имеют наибольшее значение.

В сечении действуют два изгибающих момента M_x= 9,6 кНм и M_y = 5,7 кНм, векторная диаграмма которых показана на рис. 7.31.3.

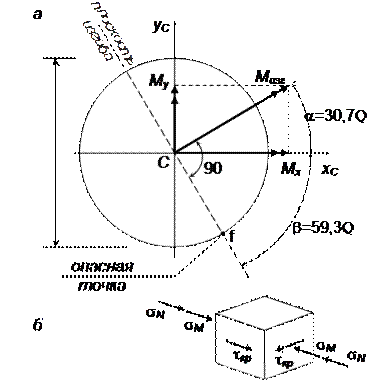
Рис. 7.31.3. Опасное сечение A₀: а – к определению положения опасной точки;

б – напряженное состояние в опасной точке

Результирующий изгибающий момент для круглого сечения

и в точке f вызывает нормальное напряжение

Плоскость изгиба проходит через центр тяжести сечения и ее положение определяется углом

3. Проверка прочности по теории наибольших касательных напряжений (третья теория прочности).

В опасной точке f, помимо напряжения σ_M, возникает нормальное напряжение от продольной силы N = –418 кН и от крутящего момента M_кр = 4,8 кНм, касательное напряжение

Полное нормальное напряжение в точке f составит

где – осевой момент сопротивления круглого поперечного сечения; – площадь поперечного сечения.

Касательное напряжение в точке f составит

где – полярный момент сопротивления.

Эквивалентное напряжение по третьей теории прочности

Прочность обеспечена с большим запасом.

Расчет брусьев прямоугольного сечения на кручение с изгибом

Рассмотрим брус прямоугольного сечения, нагруженный таким образом, что в его поперечных сечениях действуют изгибающие моменты M_z и M_y, а также крутящий момент M_x (рис. 7.32).

Рис. 7.32

Чтобы проверить прочность бруса, нужно в опасном сечении найти опасную точку, вычислить для нее эквивалентное напряжение (по одной из теорий прочности) и сопоставить его с допускаемым напряжением.

Для нахождения опасной точки сечения построим эпюры напряжений от всех силовых факторов (рис. 7.33).

Эпюры нормальных и касательных напряжений наглядно показывают, что, в отличие от круглого сечения, точки, в которых имеют место максимальные нормальные и максимальные касательные напряжения, не совпадают. В следствие этого, условие прочности составляют, как минимум для трех наиболее опасных точек поперечного сечения.

Опасной точкой по нормальным напряжениям является точка С, в которой от M_y и от M_z положительны, или точка A, в которой от M_y и от M_z также одного знака, но отрицательны. Касательные напряжения от крутящего момента в этих точках равны нулю. Таким образом, в этих точках имеет место линейное напряженное состояние.

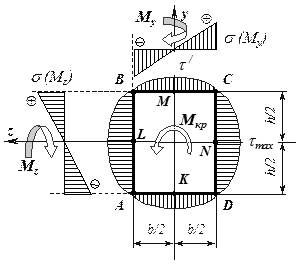
Рис.7.33

Опасной точкой по касательным напряжениям является точка N (или L), лежащая в середине длинной стороны прямоугольника. Кроме того, в этой точке действуют максимальные нормальные напряжения от изгибающего момента M_y.

Следует отметить, что в точке M (или K), расположенной в середине короткой стороны также действуют касательные напряжения (несколько меньшие ) и максимальные нормальные напряжения от M_z.

Таким образом, в точках поперечного сечения N, M, (L, K) имеет место плоское напряженное состояние, которое обуславливает использование гипотез прочности при расчетах на прочность. Для пластичных материалов применяют III (наибольших касательных напряжений) и IV (энергетическую) гипотезы прочности.

Составим условия прочности для трех предположительно опасных точек поперечного сечения

т. C:

т. N:

т. M:

Расчетная формула по четвертой гипотезе прочности

Расчет балок переменного сечения

Подбор сечений балок равного сопротивления

Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко.

Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля.

Так как изгибающие моменты обычно меняются по длине балки то, подбирая ее сечение по наибольшему изгибающему моменту, мы получаем излишний запас материала во всех сечениях балки, кроме того, которому соответствует . Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.

Условие, определяющее форму такой балки, имеет вид

Здесь М(х) и W(x) — изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту.

Эти условия справедливы и для сечения с наибольшим изгибающим моментом; если обозначить W₀ — момент сопротивления балки в сечении с наибольшим изгибающим моментом , то можно написать:

Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (рис.7.27). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.

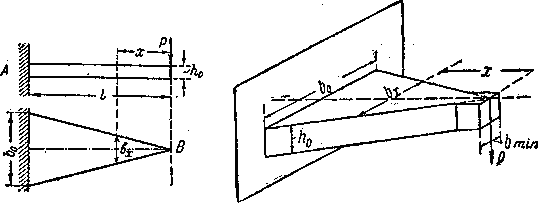
image007-28
Рис.7.34

Пусть высота балки будет постоянной , а ширина переменной b(x). Момент сопротивления в сечении на расстоянии х от свободного конца будет , а изгибающий момент M= -Px; момент сопротивления опорного сечения , a наибольший изгибающий момент в опорном сечении . В расчете имеют значения лишь абсолютные величины М(х) и

По формуле (7.40) получаем:

откуда

т. е. ширина меняется по линейному закону в зависимости от х. При x=l ширина равна .

Вид балки в фасаде и плане показан на рис.7.34. Такое очертание балки получается, если учитывать ее прочность только по отношению к нормальным напряжениям; ширина b(x) в сечении В обращается в нуль.

Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения

или, так как

Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.

Определение деформаций балок переменного сечения

При определении прогибов и углов поворота для балок с переменным сечением надлежит иметь в виду, что жесткость такой балки является функцией от х. Поэтому дифференциальное уравнение изогнутой оси принимает вид

где J(x) — переменный момент инерции сечений балки.

До интегрирования этого уравнения можно выразить J(x) надлежащей подстановкой через J, т. е. через момент инерции того; сечения, где действует ; после этого вычисления производятся так же, как и.для балок постоянного сечения.

Покажем это на примере, разобранном выше. Определим прогиб балки равного сопротивления, защемленной одним концом, нагруженной на другом конце силой Р и имеющей постоянную высоту. Начало координат выберем на свободном конце балки.

Тогда

Дифференциальное уравнение принимает вид:

Интегрируем два раза:

Для определения постоянных интегрирования имеем условия: точке А при x=l прогиб y=0 и угол поворота или

отсюда

Выражения для y и принимают вид;

Наибольший прогиб на свободном конце балки В получится при x=0: он равен

Если бы мы всю балку сделали постоянного сечения с моментом инерции J, то наибольший прогиб был бы

т. е. в 1,5 раза меньше.

Таким образом, балки переменного сечения обладают большей гибкостью по сравнению с балками постоянной жесткости при одинаковой с ними прочности. Именно поэтому, а не только ради экономии материала, они и применяются в таких конструкциях, как рессоры.

Вопросы для самопроверки

- Что такое сложное сопротивление стержней?

- Какие виды деформации бруса называют сложным сопротивлением?

- Сформулируйте принципы, на которых строится расчет брусьев при сложном сопротивлении?

- В чем заключается принцип независимости действия сил (принцип суперпозиции)?

- Как формулируется принцип Сен-Венана?

- Опишите методику определения компонентов внутренних сил при сложном сопротивлении?

- Получите формулу нормальных напряжений при сложном сопротивлении?

- Дайте определение нулевой линии и опишите способы ее построения и эпюры нормальных напряжений при сложном сопротивлении?

- Какие внутренние усилия возникают в стержне в наиболее общем случае сложного сопротивления?

- В каком случае изгиб называют плоским, в каком пространственным?

- Может ли пространственный изгиб быть прямым?

- Какой изгиб называется косым?

- Может ли балка с сечением правильной формы испытывать косой изгиб?

- Может ли косой изгиб быть плоским?

- Когда возникает косой изгиб? Опишите порядок расчета брусьев при косом изгибе?

- Сочетанием каких видов изгиба является косой изгиб?

- Применимо ли определение “косой изгиб” для балки круглого поперечного сечения? Обоснуйте.

- Как определяется положение нейтральной оси при косом изгибе?

- Проходит ли нейтральная ось при косом изгибе через центр тяжести сечения? Обоснуйте.

- Какие точки сечения будут опасными при косом изгибе?

- Как определяют перемещения при косом изгибе?

- К каким равнодействующим приводятся внутренние силы при косом изгибе?

- Для каких форм поперечных сечений балок косой изгиб невозможен?

- Как записывают условия прочности при косом изгибе для балки из пластичного материала?

- При каких формах поперечных сечений опасную точку можно определить без построения нейтральной линии при косом изгибе?

- По каким формулам определяются нормальные напряжения в поперечных сечениях балки при косом изгибе?

- Как находится положение нейтральной оси при косом изгибе?

- Как определяются опасные точки в сечении при косом изгибе?

- Как определяются перемещения точек оси балки при косом изгибе?

- Как определяется величина прогиба балки при косом изгибе?

- Как определить положение наиболее напряженной (опасной) точки бруса при косом изгибе?

- Как составить условие прочности при косом изгибе для бруса, имеющего точки сечения, максимально удаленные от обеих главных осей?

- Как определить перемещение сечения бруса при косом изгибе?

- Как определяются прогибы бруса при косом изгибе?

- Докажите ортогональность вектора прогиба и нулевой линии?

- Какой вид сложного сопротивления называется внецентренным растяжением (или сжатием)?

- В каких случаях внецентренно сжатые стержни считают жесткими, в каких гибкими?

- К каким равнодействующим приводятся внутренние силы при внецентренном растяжении (или сжатии)?

- Какие виды напряжений испытывает сжимаемый стержень при внецентренном приложении сжимаемой или растягиваемой нагрузки?

- По каким формулам определяются нормальные напряжения в поперечных сечениях стержня при внецентренном растяжении и сжатии? Какой вид имеет эпюра этих напряжений?

- Получите формулу нормальных напряжений при внецентренном действии продольной силы?

- Как определяется положение нейтральной оси при внецентренном растяжении и сжатии? Запишите соответствующие формулы.

- Какова зависимость положения нейтральной линии при внецентренном сжатии от места приложения силы?

- Проходит ли нейтральная ось при внецентренном растяжении через центр тяжести сечения? Обоснуйте.

- Чему равно нормальное напряжение в центре тяжести сечения при внецентренном растяжении?

- Могут ли при внецентренном растяжении возникать сжимающие напряжения в точках поперечного сечения?

- Как определить положение наиболее напряженной (опасной) точки сечения бруса при внецентренном растяжении (сжатии)?

- Как составить условие прочности бруса при внецентренном растяжении (сжатии)?

- В каких точках поперечного сечения внецентренно сжатого (растянутого) стержня могут возникнуть наибольшие растягивающие или сжимающие нормальные напряжения?

- Докажите свойства нулевой линии и опишите ее построение при внецентренном действии продольной силы?

- Какое положение занимает нулевая линия, когда центр давления лежит на контуре ядра сечения, на контуре сечения?

- Что такое ядро сечения?

- Какими будут напряжения во всех точках сечения если известно, что след растягивающей силы находится внутри ядра сечения?

- Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?

- Как находятся опасные сечения бруса круглого сечения при изгибе с кручением?

- Какие напряжения испытывают вал и ось? Чем они принципиально отличаются?

- Какое напряженное состояние возникает в поперечном сечении вала при совместном действии изгиба и кручения?

- Какие напряжения возникают в поперечном сечении бруса при одновременном кручении и изгибе?

- Какие точки круглого бруса являются опасными и какое напряженное состояние в этих точках при кручении с изгибом?

- Как выполняют проверку безопасной прочности при кручении с изгибом круглого бруса?

- Запишите выражения для эквивалентных моментов по различным гипотезам прочности, используемые при расчете бруса круглого сечения на прочность при одновременном изгибе и кручении?

- Напишите условие прочности для расчета вала?

- Как выбирается опасное сечение при расчете вала?

- Почему при изгибе с кручением и сочетании продольной силы с кручением расчет производится с использованием теорий прочности?

- В каких местах находятся опасные точки в брусе кругового сечения при сочетании продольной силы с кручением и изгиба с кручением?

- Получите выражения для главных напряжений в опасных точках при сочетаниях продольной силы с кручением и изгиба с кручением?

- Почему обычно не учитывают касательные напряжения от изгиба при расчете стержней на изгиб с кручением?

- Какие напряжения возникают в сечении вала в нагруженном состоянии?

- Какие теории прочности используются при расчете валов?

- Напишите расчетную формулу для определения диаметра вала?

- Почему согласно ГОСТу диаметр вала принимается кратным пяти?

- Какие точки круглого поперечного сечения являются опасными при изгибе с кручением? Какое напряженное состояние возникает в этих точках?

- Какие напряженные состояния в точке называют равноопасными?

- Какую точку принимают за опасную в прямоугольном сечении в общем случае сложного сопротивления?

- Что представляет собой эквивалентное напряжение?

- Какое напряженное состояние принимают за предельное?

- Какое напряжение принимают за предельное для пластичных материалов?

- Какое напряжение принимают за предельное для хрупких материалов?

- Что такое теории прочности и для какой цели они применяются?

- Чем отличаются между собой различные теории прочности?

- Какое назначение имеют теории предельных напряженных состояний (гипотезы прочности)?

- В чем заключается сущность теории прочности максимальных касательных напряжений и энергетической теории прочности?

- Напишите формулы для расчета эквивалентных напряжений при расчетах по теории максимальных касательных напряжений и теории энергии формоизменения? Поясните, как ими пользоваться?

- Как формулируется теория прочности наибольших касательных напряжений и условие прочности по ней?

- Как формулируется теория прочности удельной потенциальной энергии, идущей на изменение формы и условие прочности по ней?

- Напишите формулы для расчета эквивалентного момента при расчете по гипотезе максимальных касательных напряжений и гипотез энергии формоизменения?

- В чем состоит теория прочности Мора?

- В чем преимущество гипотезы прочности Мора?

- Для каких материалов и напряженных состояний можно использовать теорию прочности Мора?

- Понятие о теориях (гипотезах) прочности.

- Какие теории (гипотезы) прочности применяются наиболее часто?

- Что представляют собой теории прочности?

- Для чего служат теории прочности?

- Сформулируйте первую и вторую теории прочности. Укажите область применения.

- Сформулируйте третью и четвертую теории прочности? Укажите область применения этих теорий.

- Какие теории прочности считаются классическими?

- На каких предположениях основаны первая, вторая, третья, четвертая и пятая теории прочности? Кто является их основоположниками?

- Что положено в основу сравнения двух напряженных состояний в гипотезах прочности? Почему сложное напряженное состояние обычно сравнивается с одноосным?

- Какие теории прочности считаются рабочими?

- Какая из теорий используется при расчете конструкций из анизотропных материалов?

- Какой критерий равноопасности положен в основу теории максимальных нормальных напряжений? В каких случаях находит применение эта теория?

- Какой критерий равноопасности устанавливается в теории наибольших деформаций? В каких случаях она даст удовлетворительные результаты?

- На основе какого критерия строитеся теория максимальных касательных напряжений? Для каких материалов она нашла широкое применение в расчетах?

- Какой критерий равноопасности положен в основу энергетической теории прочности? Для каких материалов она используется?

- Какой подход положен в основу теории предельных состояний? Как для заданного напряженного состояния здесь определяется предельное состояние? Для каких материалов и напряженных состояний эта теория дает наилучшие результаты?

- Вычислите эквивалентный момент по третьей теории прочности? Изгибающий момент в поперечном сечении вала М_и=4000 Нм. Крутящий момент в том же сечении М_к=3000 Нм. Определите диаметр вала, приняв допускаемое напряжение =100 МПа?

- Как составить условие прочности для бруса круглого поперечного сечения в общем случае деформации?

- Определить внутренние усилия и перемещения прямого бруса, нагруженного вертикальной и горизонтальной силами одинаковой величины P, перпендикулярными оси бруса. Поперечное сечение бруса – квадрат со стороной b, модуль Юнга – E.

- Определить внутренние усилия и перемещения бруса прямоугольного сечения, нагруженного по верхней грани касательной нагрузкой τ_П, Па. Длина бруса l, модуль Юнга E.

- Определить внутренние усилия и перемещения консольного бруса AB прямоугольного сечения, нагруженного растягивающей силой P с эксцентриситетом e. Длина бруса l, модуль Юнга E.

- Найти внутренние усилия и перемещения горизонтальной балки круглого сечения, имеющей удельный вес γ и нагруженной на свободном конце крутящим моментом L. Модуль Юнга и модуль сдвига равны E, G. Размеры указаны на рисунке.

- Найти внутренние усилия и перемещения вертикальной балки круглого сечения, имеющей удельный вес γ и нагруженной на свободном конце крутящим моментом L. Модули Юнга и сдвига равны E и G, размеры указаны на рисунке.

- На круглый вал диаметром d насажены два колеса диаметром D₁ и D₂, на которые действуют вес груза P₁ и уравновешивающая сила P₂, как показано на рисунке. Определить величину силы P₂, внутренние усилия и перемещения вала, полагая известными вес P₁, модуль Юнга E, модуль сдвига G и длину l.

- Два шкива одинакового диаметра D насажены на круглый вал диаметром d и передают мощность W при постоянной скорости вращения ω. Натяжение ведущего ремня вдвое больше натяжения ведомого ремня: T₁=2T₂. Определить силы натяжения, внутренние усилия и перемещения вала, полагая известными модуль Юнга E, модуль сдвига G и длину l.

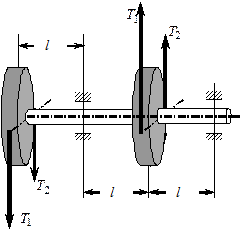
- Жесткий брус нагружен силами F₁и F₂. Построить эпюры нормальных напряжений по подошве бруса от действия каждой силы отдельно.

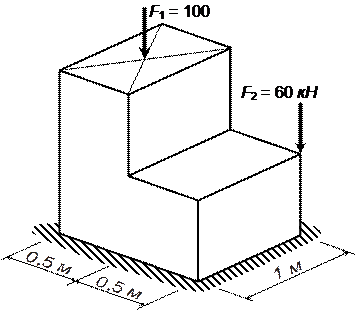
- Сравнить наибольшие нормальные напряжения в стержне AB по сечениям I-I и II-II.

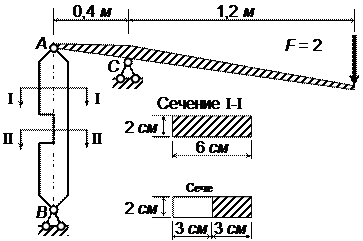
- Для двутавровой консоли №20:

1) построить эпюру нормальных напряжений в опасном сечении;

2) определить величину и направление полного прогиба конца балки.

- Вал трубчатого сечения имеет два шкива диаметрами D₁= 0,3 м, D₂= 0,5 м и передает мощность W = 200 кВт при n = 300 об/мин. Считая, что натяжение ветвей ременных передач T_i = 2t_i, по третьей теории прочности подобрать размеры сечения при [σ] = 120 МПа.

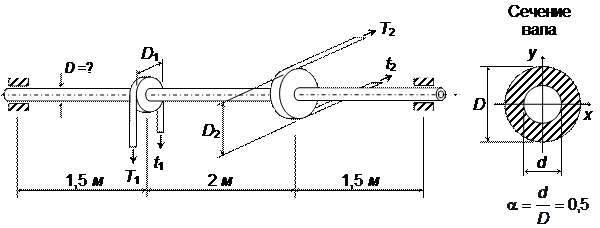
email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00