Главная

Лекция 14 (продолжение). Метод перемещений при расчете статически неопределимых систем

Содержание

Неизвестные метода перемещений

Выбор основной системы

Сущность метода перемещений

Элементарные состояния основной системы

Определение коэффициентов канонических уравнений

Определение усилий и построение эпюр

Алгоритм метода перемещений

Примеры расчета рам методом перемещений

Вопросы для самопроверки

Принципиальная схожесть метода сил и метода перемещений состоит в том, что в обоих случаях выбирается основная система и в процессе устранений противоречий между основной системой и рамой, которую нужно рассчитать, решают задачу о нахождении расчетных усилий М, Q и N.

Как уже знаем, при расчете статически неопределимых систем методом сил исключаются лишние связи, а за неизвестные принимаются силы (усилия) в этих связях. После их вычисления из канонических уравнений можно определять все остальные усилия, а также перемещения, напряжения и деформации системы.

Можно решить задачу раскрытия статической неопределимости иначе: сначала найти перемещения характерных точек упругой системы, а затем внутренние силовые факторы. Метод перемещений отличается от метода сил тем, что за основные неизвестные принимаются перемещения узлов стержневой системы (углы поворота и линейные перемещения). Поэтому особенно просто раскрывается статическая неопределимость системы с малым числом узлов.

Неизвестные метода перемещений

Установим минимальное число узловых перемещений, необходимых для определения напряженно-деформированного состояния статически неопределимой стержневой системы.

С этой целью определим простейшие деформации некоторого стержня АВ стержневой системы, которые он получает при переходе в новое положение под воздействием внешней нагрузки (рис. 1,а). Данная задача упрощается, если стержень закрепить по обоим концам и, задавая его концам некоторые независимые перемещения, привести стержень к окончательному деформированному состоянию .

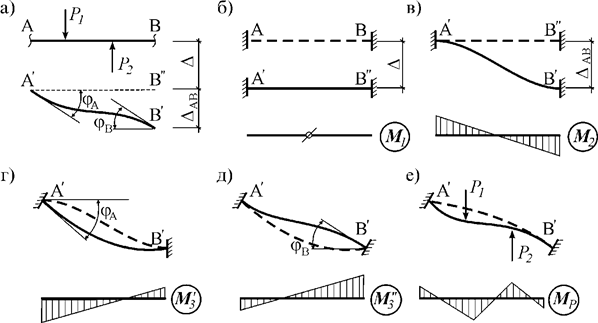
Рис. 1

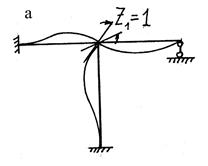
Как следует из рисунков, для этого концам закрепленного стержня АВ необходимо последовательно задавать поступательные (линейные) перемещения и (рис. 1,б, в), угловые перемещения и (рис. 1,г, д), а внутри стержня приложить внешнюю нагрузку (рис. 1,е).

При этом от поступательного перемещения ∆ всего стержня внутренние усилия и деформации не возникают (на рис. 1,б ). Внутренние усилия и деформации от местной нагрузки, действующей в пределах закрепленного стержня АВ, можно найти отдельно. Значит, для определения НДС всего стержня достаточно знать три неизвестных перемещения – два угловых перемещения его концов и и одно поступательное перемещение – взаимное смещение концов стержня . Поэтому степень кинематической неопределимости такого стержня равняется трем.

Выбор основной системы

Основная система метода перемещений должна быть кинематически определимой. Значит, для ее получения в заданную систему следует ввести столько дополнительных связей, чтобы концы всех стержней были закреплены и исключены их перемещения. Поэтому общее число вводимых связей будет равно числу неизвестных метода перемещений.

Однако число вводимых связей (а значит и число неизвестных метода перемещений) может быть весьма большим. Например, рама на рис.2,а состоит из пяти стержней. По результатам проведенного выше анализа, степень ее кинематической неопределимости (или число неизвестных метода перемещений) будет 53=15.

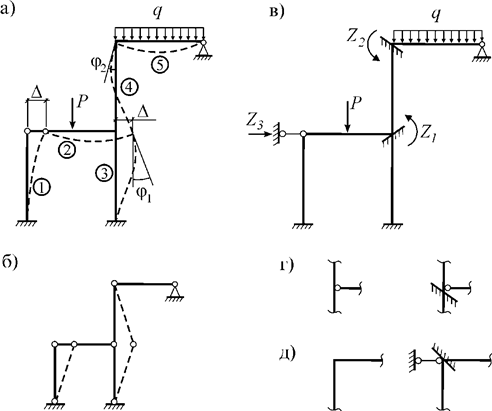
Рис. 2

Это число можно уменьшить, если принять следующие гипотезы:

1) поперечные и продольные деформации стержней малы;

2) длина хорды, соединяющей концы изогнутого стержня, равна первоначальной длине стержня;

3) влиянием поперечных и продольных сил на величину перемещений пренебрегают;

4) в рамах с несмещающимися узлами рассматривают только угловые перемещения; в рамах со смещающимися узлами – угловые и линейные;

5) полагают, что концы стержней, сходящихся в одном узле, поворачиваются на один и тот же угол;

6) углы поворота, в силу их малости, принимают равными их тангенсам.

Действительно, в этом случае в данной раме достаточно будет знать только три перемещения – поступательное перемещение и два угловых перемещения и (рис. 2,а). Таким образом, число неизвестных уменьшилось намного – с пятнадцати до трех.

Из третьей гипотезы следует, что число неизвестных угловых перемещений будет определяться по формуле

= числу упругих рамных узлов.

Для определения числа неизвестных поступательных перемещений (в дальнейшем их будем называть линейными перемещениями) во все узлы рамы, включая и опоры, нужно ввести шарниры (рис. 2,б). Тогда число линейных перемещений будет легко определяться по известной формуле кинематического анализа для фермы

В рассматриваемой раме имеем

Или для рамы

n_лин=3D - 2Ш - С₀.

Можно определить n_лин и без формулы. Для этого нужно “подергать” каждый узел вдоль примыкающего к нему стержня и в поперечном направлении. Нетрудно увидеть, в каком направлении перемещение возможно за счет возникающего при этом изгиба элементов рамы. При этом нужно иметь ввиду, что введенные заделки запрещают только поворот, но не препятствуют линейным перемещениям узлов. Поэтому заделки называют “плавающими”. Подсчитывая число возможных перемещений, определяют n_{л .}

Общее число всех неизвестных перемещений определяется по формуле

и называется степенью кинематической неопределимости. Сами неизвестные перемещения обозначаются однотипно:

После определения числа неизвестных в ЗС следует вводить столько же связей для исключения перемещений концов ее стержней. Например, в рассмотренную раму введем две заделки и одну опорную связь. Полученная схема (рис. 2,в) будет основной системой (ОС) метода перемещений.

Таким образом, для получения ОС метода перемещений необходимо:

– в упругие рамные узлы заданной системы ввести заделок;

– в направлении поступательных перемещений узлов заданной системы ввести опорных связей (они вводятся так, чтобы система с введенными шарнирами стала геометрически неизменяемой).

То есть в раме с несмещающимися узлами основную систему получают наложением на жесткие узлы дополнительных закреплений, препятствующих только повороту узлов. В раме же со смещающимися узлами, кроме наложения закреплений на жесткие узлы, требуется установка и дополнительных стержней, закрепляющих раму от возможных линейных перемещений. Основная схема метода перемещений – единственная.

Введенные связи, хотя внешне и похожи на обычные опорные связи, от них принципиально отличаются, потому что: 1) введенная заделка исключает лишь угловое перемещение узла, оставляя возможность линейного смещения; 2) введенная опорная связь исключает только линейное перемещение узла, оставляя возможность поворота (рис. 2,г, д).

При соблюдении этих требований ОС метода перемещений будет единственной.

Пусть необходимо выбрать ОС метода перемещений для рамы (рис.3,а). Она имеет четыре жестких узла. Значит, число угловых неизвестных . Для определения числа линейных неизвестных во все узлы и опоры рамы введем шарниры (рис.3,б). Тогда имеем: Поэтому общее число неизвестных будет Вводя в жесткие узлы ЗС четыре заделки и две опоры, исключающие линейные перемещения узлов рамы (последние вводятся так, чтобы механизм на рис. 3,б стал геометрически неизменяемым), получаем требуемую ОС (рис.3,в).

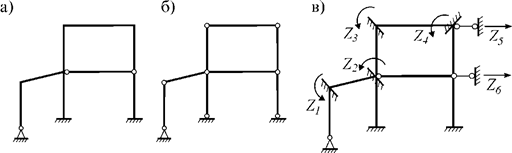
Рис. 3

Для другой приведенной рамы (рис. 3.1,а) основная система показана на рис. 3.2. Для данной рамы n_угл. всегда равно количеству жестких узлов конструкции (на рисунке 3.1,а один жесткий узел 1), то n_лин. равно степени свободы шарнирной схемы конструкции (рамы). Для получения шарнирной схемы рамы вводятся шарниры во все жесткие узлы рамы, включая и жесткие заделки (опоры) (рис. 3.1,б). Для полученной рамы подсчитываем степень свободы:

Результат еще не означает, что n_лин. = 0. Необходимо провести анализ полученной конструкции. Заметим, что шарниры 0, 1, 4 лежат на одной прямой, что означает – система мгновенно изменяемая, узел 2 при этом не ликвидирует этого дефекта. Нам необходимо поставить опорный стержень по горизонтали в узел 1 или в узел 2 и тогда:

Общее число неизвестных n будет равно 2 – по количеству введенных связей.

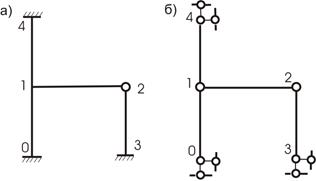
Рис.3.1

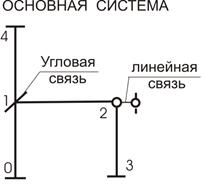
Рис.3.2

Для рамы (рис. 3.3) основная система приведена на рис.3.4. Здесь установлено три жесткие связи и две линейные в виде опорных стержней. И мы получили:

Количество введенных связей в конструкцию (раму) определяет и степень кинематической неопределимости рамы. В первом примере она равна 2, во втором – 5. В каждой введенной связи возникают реактивные усилия: в заделке - только момент (заделка не препятствует линейному смещению!), а в линейных связях - только реакция (усилие) по направлению этой связи.

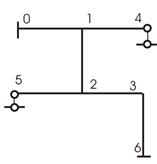
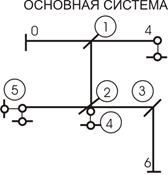
Рис.3.3 Рис.3.4

Рассмотрим еще примеры расчета неизвестных перемещений и определения основных систем приведенных рам (рис.3.5,а,б).

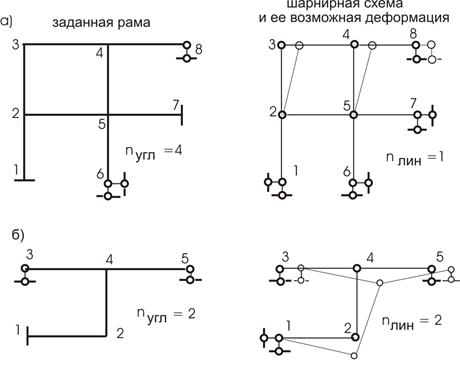
Рис.3.5

Итак, для рамы (рис. 3.5,а) имеем 4 жестких узла (2, 3, 4, 5), что дает

Шарнирная схема дает

Одно линейное смещение и возможная при этом деформация рамы приведены на схеме (рис. 3.5,а). Для рамы (рис. 3.5,б) имеем 2 жестких узла (2, 4), что определяет , а шарнирная схема дает две степени свободы, что определяет .

N = 10 – 4 – 4 = 2

Нужно отметить, что если n=0 и система полностью или ее участок мгновенно-изменяем, что требует постановки связи, то будет равно количеству линейных связей, устанавливаемых в шарнирную схему конструкции для обеспечения ее неизменяемости и неподвижности (рис. 3.6).

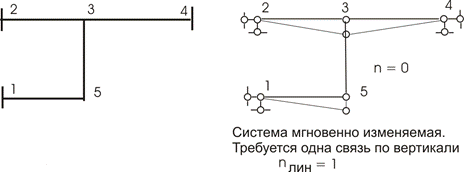
Рис.3.6

Основные системы для рам (рис.3.5, а,б), показаны на рисунке 3.7. Нумерация связей обозначена в кружочках.

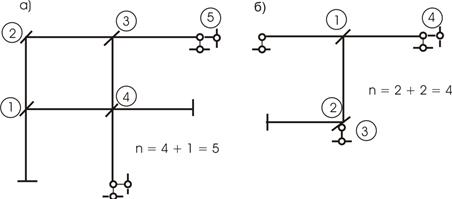
Рис.3.7

Определим, например, степень кинематической неопределимости рамы, изображенной на рис.3.8,а. В раме четыре жестких узла: n_y = 4. На рис.3.8,b показана шарнирная система. Определяем число ее степеней свободы:

Следовательно , степень кинематической неопределимости рамы равна

n = 4+2 = 6.

На рис. 3.8,с показана основная система метода перемещений.

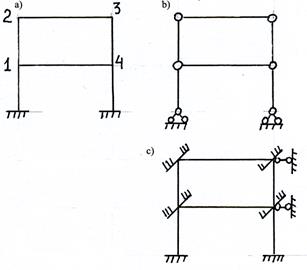
Рис.3.8

Рассмотрим портальную раму на рис.4.

а) б) в)

Рис. 4

Внешние моменты в узлах считаем положительными при их вращении по часовой стрелке. Это же правило принимаем для углов поворота узлов. Рама три раза статически неопределима. Число жёстких узлов . Чтобы найти , заменим все жёсткие узлы и жёсткие защемления шарнирами и превратим систему в геометрически изменяемую, т.е. механизм (рис.4,б). Число независимых линейных перемещений определится как число простых связей, которые необходимо наложить на шарнирную схему конструкции, чтобы сделать её геометрически неизменяемой. В данном примере (рис.4, б). Таким образом, число неизвестных перемещений n = 2+1 = 3, т.е. столько же, сколько и по методу сил.

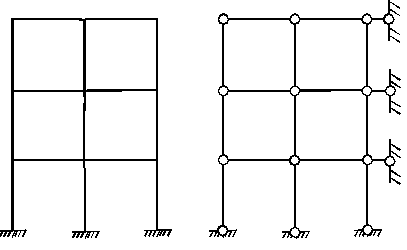
Усложним раму (рис.5), число узлов , число простых дополнительных внешних связей . Следовательно, число неизвестных перемещений по методу перемещений n = 9+3 = 12. По методу сил число неизвестных .

а) б)

Рис. 5

Если к основной системе приложить внешние силы (рис. 5.1, в), то получим систему эквивалентную заданной на основании принципа независимости действия сил.

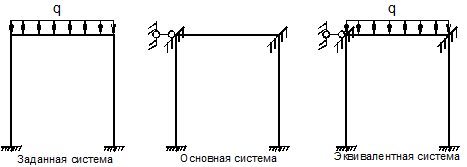
а) б) в)

Рис. 5.1

Сущность метода перемещений

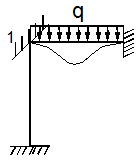
Данный вопрос изучим на следующем примере (рис. 6,а). Эта рама четырежды статически неопределима. При ее расчете методом сил нужно исключать четыре лишние связи и выбирать основную систему, например, такую как на рис. 6,б.

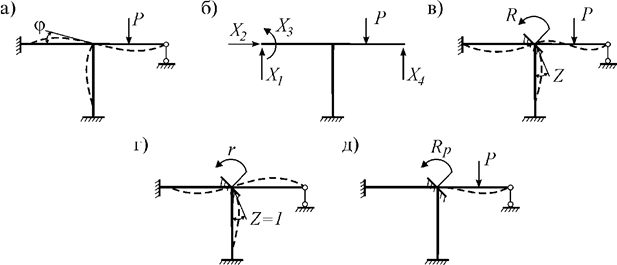
Рис. 6

При использовании же метода перемещений раму следует превратить в кинематически определимую. Для этого в ЗС достаточно ввести кинематическую связь. Если неизвестное угловое перемещение узла обозначить через Z, получим ОС показанную на рис. 6,в.

Потребуем, чтобы усилия и деформации ОС были такими же как у ЗС. Для этого перемещение Z должно быть равно углу поворота узла рамы (рис. 6,а), а реактивный момент во введенной заделке основной системы (рис. 6,в) должен равняться нулю:

R =0.

Эту реакцию определим, рассматривая единичное и грузовое состояния основной системы.

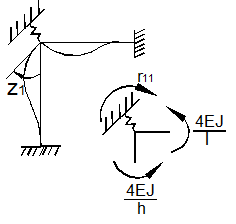
В единичном состоянии введенной связи зададим единичное перемещение Z=1 и определим возникающую в ней реакцию r (рис. 6,г). Такая реакция от единичного перемещения называется жесткостью.

В грузовом состоянии приложим только внешнюю нагрузку и во введенной связи основной системы определим реакцию R_P (рис. 6,д).

С учетом упругости системы и принципа суперпозиции наше уравнение приводится к виду

r  Z+ R_P =0.

Оно называется каноническим уравнением метода перемещений. Если известны реакции r и R_P, то из него можно найти величину узлового перемещения:

Z= – R_P /r.

Если степень кинематической неопределимости стержневой системы равна n, ее ОС получается введением n дополнительных связей с неизвестными Z₁, Z₂, …, Z_n. Чтобы ОС была эквивалентна ЗС, реакции во введенных связях должны равняться нулю. С учетом этого можно записать n уравнений. После рассмотрения n единичных состояний, одного грузового состояния и дальнейшего определения реакций (реактивных усилий) во всех состояниях, эти уравнения приводятся к следующему виду:

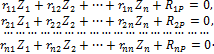
Все вместе они называются системой канонических уравнений метода перемещений. Здесь – главные (основные) коэффициенты, – боковые (побочные) коэффициенты (коэффициенты жесткости). Свободные члены являются грузовыми коэффициентами.

Выясним статический смысл коэффициентов . Дадим, например узлам системы (рис. 6.1, а) перемещения Тогда из системы канонических уравнений следует:

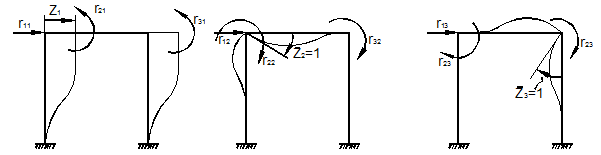
а) б) в)

Рис. 6.1

Таким образом, – это обобщённые силы, которые нужно приложить в узлах в направлении неизвестных перемещений, чтобы получить единичное перемещение узла

Аналогично выясняется смысл остальных коэффициентов жёсткости . Итак, – это обобщённые силы, приложенные в узлах номер i (i = 1,2,…,n) при единичном перемещении , т.е. узла j. Такая трактовка справедлива только для упругих систем.

Элементарные состояния основной системы

Как было указано в предыдущем пункте, коэффициенты системы канонических уравнений метода перемещений – реакции, определяемые в единичных и грузовом состояниях. Например, – реакция, возникающая в i-ой связи в j-ом единичном состоянии, – реакция, возникающая в i-ой связи в грузовом состоянии.

Все эти реакции равны сумме реакций отдельных стержней, объединяемых в узлах основной системы. Для их определения необходимо рассчитывать статически неопределимые стержни различной длины и жесткости с различными закреплениями по концам, получающие разные перемещения или нагруженные различными силами. С целью упрощения таких расчетов все типовые задачи, встречающиеся при расчете различных основных систем, решаются для общего случая. Их называют элементарными состояниями основной системы, а результаты их расчетов сводятся в таблицу. Эти задачи в большинстве случаев бывают статически неопределимыми и поэтому решаются методом сил.

Рассмотрим решение двух типовых задач.

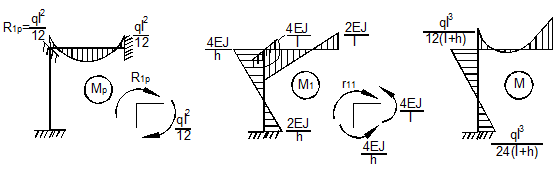
1) Стержень с равномерно распределенной нагрузкой q

Степень статической неопределимости этой системы (рис. 7,а) n=1. Каноническое уравнение имеет вид . Выбирая основную систему (рис. 7,б), в единичном (рис. 7,в) и грузовом (рис. 7,д) состояниях строим единичную (рис. 7,г) и грузовую эпюры (рис. 7,е).

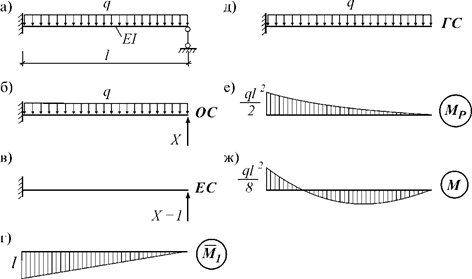
Рис. 7

Определим коэффициенты канонического уравнения:

а затем неизвестную реакцию: . После этого из уравнений статики определяем остальные реакции, а по формуле строим эпюру изгибающих моментов (рис. 7,ж).

2) Поворот одного конца стержня с заделанными концами

Пусть один конец стержня с заделанными концами поворачивается на единичный угол (рис. 8,а). У этой системы степень статической неопределимости n=3. Однако, если не учитывать продольную деформацию, вместо заданной системы можно рассматривать стержень с правой опорой в виде ползуна (рис. 8,б) и принять n=2.

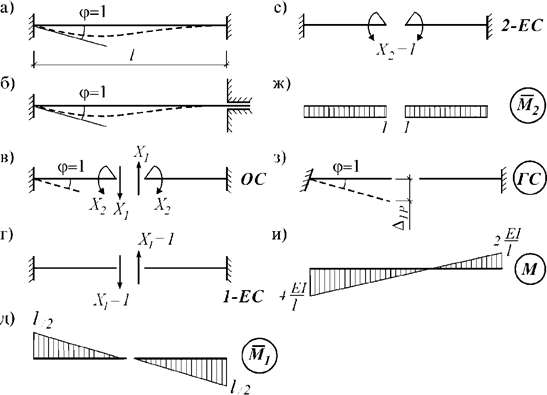
Рис. 8

Система канонических уравнений будет:

Если основную систему выбрать симметричной (рис. 8,в), в обоих единичных состояниях (рис. 8,г, е) единичные эпюры легко строятся (рис. 8,д, ж). В грузовом состоянии (рис. 8,з) момент не возникает, поэтому

Определим коэффициенты канонических уравнений:

Из рис. 8,з следует что и , а из канонических уравнений получаем

Так как , имеем (рис. 8,и).

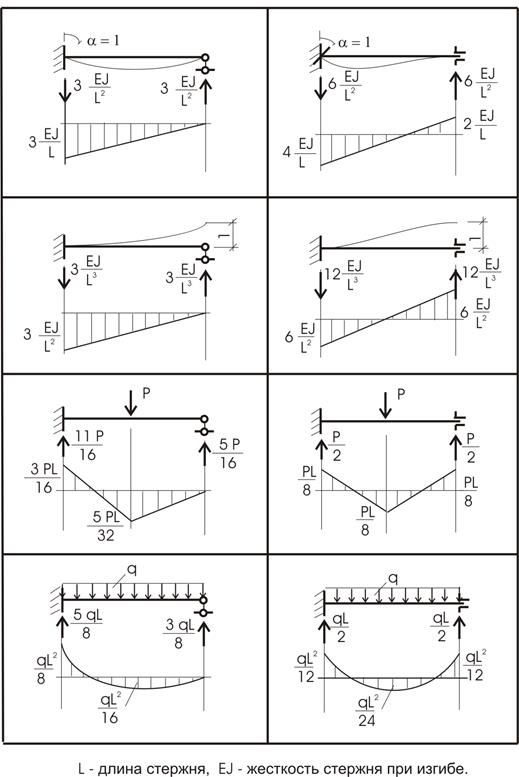
Аналогичные расчеты проводятся для всех типовых случаев, встречающихся в различных основных системах. Результаты их расчетов сводятся в единую таблицу метода перемещений (таблица 1).

Таблица 1. Реакции опор и величины изгибающих моментов от перемещения

опор и внешней нагрузки

Определение коэффициентов канонических уравнений

Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.

Статический способ основан на определении реакций во введенных связях основной системы из уравнений статики. Для этого необходимо вырезать отдельные узлы или части основной системы и составлять уравнения равновесия (статики). Если искомая реакция является реактивным моментом, то она определяется из условия равенства нулю момента в узле SM=0, если же она является реактивной силой, то определяется из уравнения проекции на ось (например, на ось x) в направлении этой реакции . Статический способ достаточно прост для использования, поэтому является основным способом определения коэффициентов системы канонических уравнений.

Докажем одну полезную теорему.

Теорема Релея. Реакция, возникающая в j-ой связи от перемещения i-ой связи на единицу, равна реакции i-ой связи от перемещения j-ой связи на единицу, т.е. .

Доказательство. Рассмотрим i-ое и j-ое единичные состояния основной системы некоторой рамы (рис. 9,а, б) и соответствующие эпюры моментов в этих состояниях (рис. 9,г, д).

Возможная работа сил j-ого единичного состояния (рис. 9,б) на перемещениях i-го состояния (рис. 9,а) равна

Работа сил i-го состояния на перемещениях j-го состояния будет

По теореме Бетти . Значит, равны и правые части, т.е. .

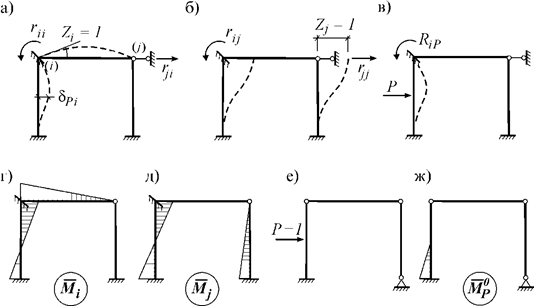
Рис. 9

Эту теорему иногда называют теоремой о взаимности реакций. Она позволяет сократить объем вычислений побочных коэффициентов канонических уравнений.

Кинематический способ основан на определении коэффициентов канонических уравнений перемножением эпюр. Этот способ применяется при сложности определения коэффициентов статическим способом или для проверки результатов статического способа.

Для вывода формулы кинематического способа определим две возможные работы. Работа внешних сил j-го единичного состояния на перемещениях i-го состояния нам известна: . А возможная работа внутренних сил j-го единичного состояния на деформации i-го состояния равна:

По принципу возможных перемещений или . Отсюда получаем искомую формулу:

Формула вычисления грузовых коэффициентов отличается от аналогичной формулы метода сил (дается без вывода):

где – грузовая эпюра изгибающих моментов в любой статически определимой системе, полученной из заданной системы удалением лишних связей.

Рассмотрим примеры вычисления коэффициентов при неизвестных на примере рисунка 9.1. Для этого строим эпюры изгибающих моментов от перемещений введенных связей на единицу.

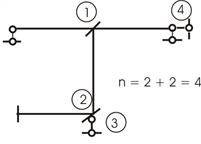
Рис.9.1

Дадим первой связи (заделке) перемещение в виде поворота ее по часовой стрелке на угол, равный 1.

Стержни, сходящиеся в узле 1 с наложенной связью (заделкой), деформируются (рис. 9.2). Следовательно, в них появятся внутренние усилия – нас интересует только изгибающий момент.

Решения каждой такой балки от подобного перемещения уже имеются, и нам нужно только ими воспользоваться (рис. 9.3).

От перемещения первой связи возникнут реактивные усилия во всех введенных связях.

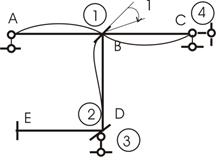
Рис.9.2

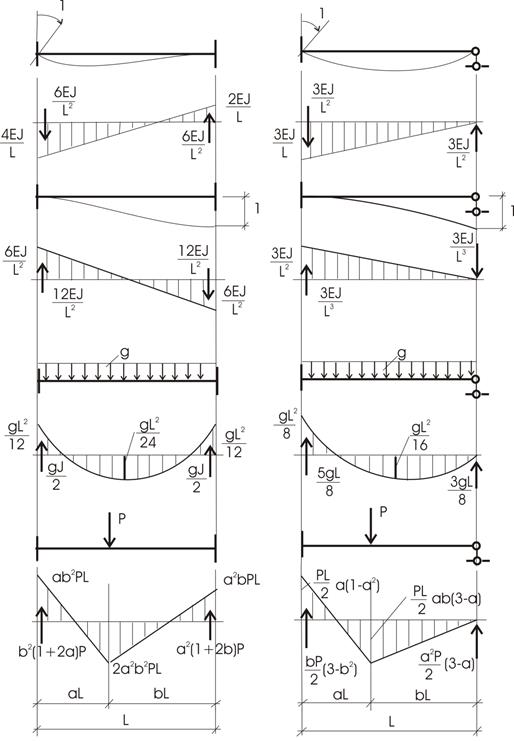
Рис.9.3

Определим величины реактивных усилий двумя способами: статическим и кинематическим:

Статический способ.

В его основе лежит метод сечений. Так, для определения , т. е. реактивного усилия в заделке (М) – первой связи - от перемещения первой связи вырежем узел В (рис. 9.4).

На узел действуют (рис. 9.5):

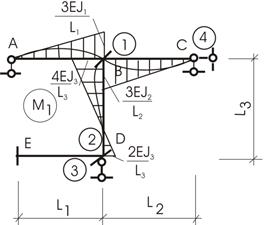
Рис.9.4

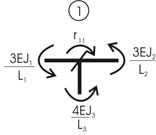
Рис.9.5

а) - реактивное усилие в заделке (связи). Если его направление совпадает с направлением перемещения, то оно – положительное;

б) - изгибающий момент в заделке со стороны стержня ВА;

в) - то же - со стороны стержня ВС;

г) - то же - со стороны стержня ВD.

Составим уравнение статики:

откуда

Для определения - реактивного усилия во второй связи от перемещения первой связи на 1 – вырежем узел D (рис. 9.6).

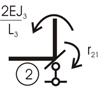
Рис.9.6

- направим по часовой стрелке (по направлению предполагаемого перемещения второй заделки – связи).

Вновь

Откуда:

Для определения реактивного усилия в третьей связи – опорном стержне – проведем сечение: по опорному стержню 3, по опорам Е, А, С. (рис. 9.7). В сечениях А, С действуют реактивные усилия и в связи 3 возникнет реакция .

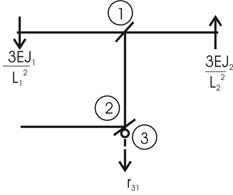
Рис.9.7

Составляем уравнение статики:

откуда

Для определения реактивного усилия проводим сечение: по стержню (связи) 4, по опоре А, по стержню BD у узла D (рис. 9.8). Направим по предполагаемому перемещению.

Составим уравнение статики:

откуда

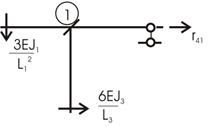
Рис.9.8

При определении реактивных усилий в линейных связях от воздействия внешней нагрузки при составлении уравнения статики , учитывается вся внешняя нагрузка (рис. 9.9), т. е.

откуда

Рис.9.9

Кинематический способ.

Он заключается в перемножении соответствующих эпюр (подобно методу сил). Этот способ не нашел практического применения из-за большой вычислительной работы, что достаточно проследить на перемножении одного участка эпюры М₁ (рис. 9.10)

Обратите внимание, что этот результат уже имеется на эпюре М₁ (рис. 9.3). При перемножении других фигур вычислений еще больше.

Рис.9.10

Подставляя вычисленные значения и в систему и решая ее, получим .

Определение усилий и построение эпюр

После определения всех коэффициентов они подставляются в систему канонических уравнений. Затем она решается и определяются неизвестные Z₁, Z₂, …, Z_n. После этого определяются внутренние усилия заданной статически неопределимой системы. Это выполняется аналогично методу сил. Вначале по формуле

определяются моменты. Затем по эпюре M определяются поперечные силы Q, а по ним – продольные силы N.

Правильность построения М (правильность решения задачи) производится кинематической проверкой, а именно, эпюра М перемножается на одну из единичных эпюр метода сил.

Алгоритм метода перемещений

Метод перемещений реализуется в следующей последовательности:

1. Определение степени кинематической неопределимости n.

где n_угл – число жестких узлов в раме, n_лин - число возможных линейных перемещений узлов и подвижных опор рамы.

Степень кинематической неопределимости равна числу неизвестных углов поворота и перемещения жестких узлов рамы Z.

2. Выбор основной системы путем введения дополнительных связей.

2.1. В каждый жесткий узел вводится “плавающая” заделка, препятствующая повороту узла, но не мешающая ее линейному перемещению (всего вводится n_угл заделок),

2.2. Вводят дополнительные опорные стержни, препятствующие линейным перемещениям узлов системы (всего вводится n_лин опор).

Таким образом, основная система метода перемещений – это система балок с закрепленными и несмещаемыми концами. В отличие от метода сил в методе перемещений возможна только одна основная система.

3. Для определения неизвестных записывают канонические уравнения метода перемещений, смысл которых состоит в том, что приравниваются нулю реакции во введенных связях, т.е. снимается противоречие между рассчитываемой и основной системой.

Для системы n раз кинематически неопределимой канонические уравнения имеют вид

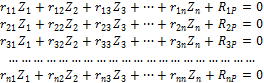
Здесь - реакция в введенной связи с индексом i от единичного перемещения связи с индексом j, R_{iP -} реакция в введенной связи с индексом i от заданной нагрузки.

На основе теоремы о взаимности реакций система симметрична относительно диагонали, то есть .

4. Рассмотрение единичных и грузового состояний.

5. Определяют коэффициенты и свободные (грузовые) члены канонических уравнений.

5.1. В основной системе последовательно строят единичные эпюры моментов М_i – эпюры изгибающих моментов от поворотов заделок на угол, равный единице и от единичных линейных перемещений по направлению введенных дополнительных опорных стержней. Эти эпюры строят при помощи таблицы 1.

5.2. В основной системе по таблицам строят грузовую эпюры М_Р от заданной нагрузки.

5.3. Вычисляют коэффициенты и свободные члены канонических уравнений, последовательно рассматривая равновесие узлов (для определения реактивных моментов) или отдельных стержней рамы (для определения реакций во введенных опорах).

6. Решают систему канонических уравнений, находят неизвестные углы поворота и перемещения узлов Z₁ ,Z₂ …

7. Построение окончательной эпюры M.

М=М_Р+М₁Z₁ + M₂Z₂ + …

Удобно вначале построить так называемые исправленные эпюры моментов М₁Z₁, M₂Z₂ …,полученные умножением ординат каждой единичной эпюры М_i на найденное соответствующее значение Z_i .Если какое либо перемещение или угол поворота Z_i получилось со знаком минус, то это означает, что исправленная эпюра должна быть построена на противоположном, чем единичная эпюра, волокне.

8. Проверка правильности расчета. Она проводится аналогично методу сил – статическим и кинематическим способами. Рассматривают равновесие моментов во всех жестких узлах рамы.

9. По эпюре моментов (по формуле Журавского) строят эпюру поперечных сил Q.

10. Из условия равновесия узлов рамы определяют продольные усилия N в ее стержнях.

11. Проводят второй этап проверки: отрезают раму от опор, прикладывают найденные продольные и поперечные силы в полученных сечениях и проверяют равновесие рамы вцелом.

Как видим, алгоритмы метода перемещений и метода сил совпадают. Но при более подробном рассмотрении можно выявить не только сходные, но и принципиально отличающиеся стороны этих методов. Рассмотрим некоторые из них:

− оба метода используются для расчета статически неопределимых систем; при принятии одинаковых допущений оба приводят к единому результату, а при использовании в разных областях дополняют друг друга;

− в методе сил неизвестными являются силы, а в методе перемещений неизвестными являются перемещения; при расчете одной и той же системы число их неизвестных часто бывает разным, поэтому одни системы выгоднее рассчитывать методом сил, другие − методом перемещений;

− в методе сил основная система получается удалением связей, а в методе перемещений – введением связей; в методе сил вариантов основной системы много, а в методе перемещений она единственна;

− единичные состояния в методе сил определяются воздействием единичных сил, в методе перемещений – единичных перемещений;

− в методе сил необходимые эпюры в основной системе строятся обычным способом, а в методе перемещений – по готовой таблице;

− коэффициенты канонических уравнений в методе перемещений определяются проще (из уравнений статики);

− многие из боковых коэффициентов системы канонических уравнений метода перемещений равняются нулю, что упрощает ее решение и т.д.

Для расчета рамы методом перемещений нужно:

1) уметь правильно выбирать основную систему и назначать неизвестные перемещения;

2) уметь строить эпюры изгибающих моментов и находить опорные реакции в балках с полностью или частично заделанными концами при различных силовых и кинематических воздействиях.

Примеры расчета рам методом перемещений

Пример 1.

Рассчитаем раму, представленную на рисунке 10.

Рис.10

Решение.

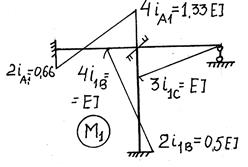
1. Число неизвестных:

(два жестких узла).

Линейные неизвестные определяются из шарнирной схемы рамы (рис. 11,а):

Узлы 1, 2, 3 находятся на одной прямой и, если не установим недостающую связь в узел 2 по вертикали, получим мгновенно-изменяемую конструкцию. Поэтому установим в узел 2 по вертикали недостающую связь. Основная системе показана на рис. 11,б (нумерация связей в кружочках)

2. Система канонических уравнений запишется:

где - реактивное усилие в первой связи от перемещения первой связи на единицу. Первая связь заделка. Значит она может поворачиваться. Даем ей поворот на . Произойдет деформация только тех стержней, которые составляют этот узел (рис. 11,в).

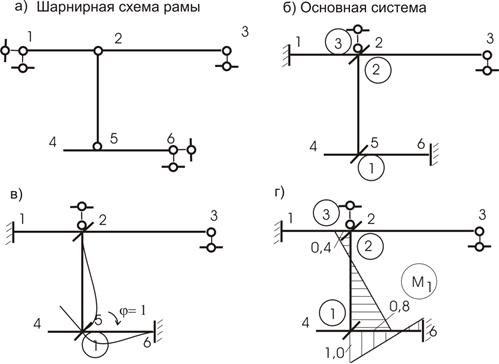
Рис.11

По деформированному состоянию строим эпюры изгибающих моментов (рис. 11,г), используя уже готовые решения (таблица 1).

Вырезая узел со связью 1 (рис. 12,а), найдем . Направление считаем положительным, если оно направлено по направлению перемещения связи:

Перемещение связи 1 вызывает реакции во введенных связях 2 и 3. Вырезаем узел со второй связью (рис. 12,б) и найдем r₂₁:

Рис.12

Для получения величины в третьей связи проводим сквозное сечение. Оно пройдет по связи 3, по опоре 1, 6, далее по опоре 3 (рис.13). Реакции в опорах 1, 3 равны нулю, а реакция в опоре 6 равна (по табличным данным). Знак или направление будет зависеть от направления перемещения третьей связи. Не будем торопиться с этим.

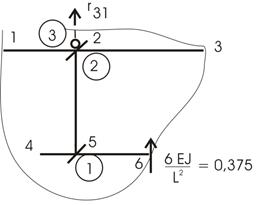
Рис.13

Дадим перемещение второй связи – угол поворота узла 2 по часовой стрелке (рис. 14), т. е. перейдем к определению величины и производных от этого перемещения. Деформируются стержни, сходящиеся в узел 2 (рис.14).

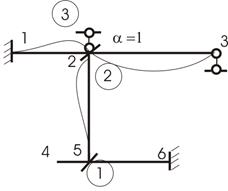
Рис.14

По табличным решениям строим эпюру М₂ (рис. 15,а).

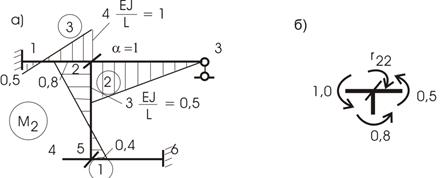
Рис.15

Вырезая узел со связью 2, из его равновесия найдем r₂₂ (рис. 15,б).

Вырезая узел 5 со связью 1, определим , но , а мы уже определили .

Читатель может еще раз проверить наши рассуждения. Мы не будем торопиться с определением .

Даем перемещение третьей связи на единицу (рис. 16).

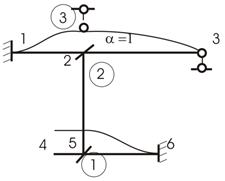
Рис.16

Теперь самое время вернуться к определению (рис. 13). Возьмем перемещение третьей связи вверх (как направили на рис.13, но это совсем необязательно). Для деформированных стержней (рис. 16) строим эпюры М, используя таблицу (рис. 17). Теперь проецируя на ось у усилия 0,375 и из рисунка 13, находим:

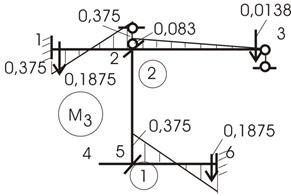
Рис.17

Проверим. Вырежем из М₃ узел 5 с первой связью (рис. 18,а):

Видим полное совпадение

Вырезая узел 2 со второй связью, найдем и (рис. 18,б):

Рис.18

Для определения проведем сечение по связи третьей и по опорам 1, 6, 3, получим (рис. 19):

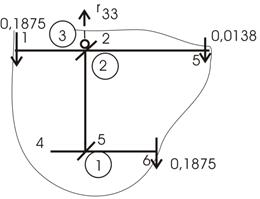
Рис.19

Коэффициенты при вычислили.

Перейдем к определению . Для этого построим эпюру М_р (рис. 20) от внешнего загружения по табличным решениям.

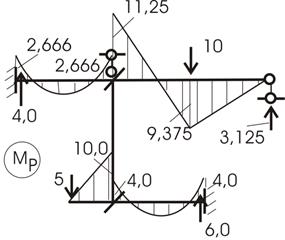
Рис.20

Определяем . Вырезаем узел 5, рис. 21,а:

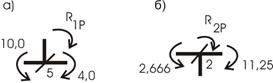
Рис.21

Определяем . Вырезаем узел 2, рис. 21,б:

Определяем (рис. 22):

откуда

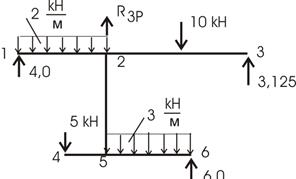
Рис.22

Система канонических уравнений готова к решению:

Из решения системы получаем:

Для построения окончательных эпюр M, Q, N воспользуемся вторым путем, как при методе сил, а именно:

Процесс построения эпюры М_ок можно проследить по рисунку 23.

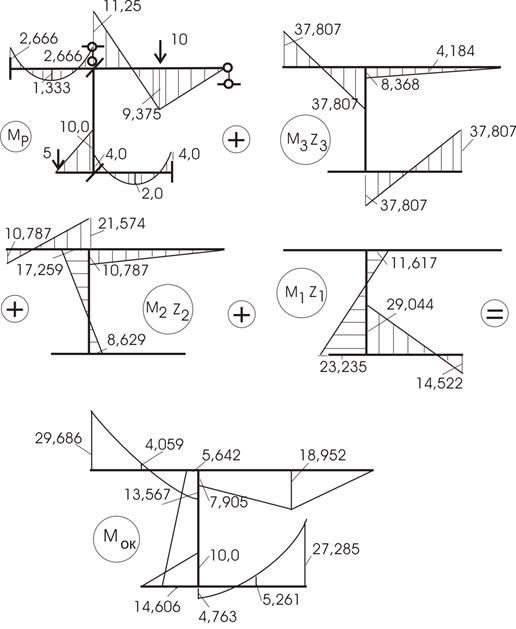
Рис.23

3. Производим проверки правильности построения эпюры М_ок:

1. Статическая (вырезаются узлы 2 и 4 – рис. 24):

13,567-7,905-5,642=0; 0,02=0.

14,606-4,763-10=0; -0,157

Грубоватый расчет.

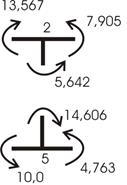
Рис.24

2. Кинематическая.

Для кинематической проверки необходимо построить эпюру М₁ для точки, заведомо зная ее перемещение. Лучше всего построить М₁ метода сил. Самое простое: выберем основную систему метода сил, оставив опору 1(заделку). Приложим к точке 3 по вертикали единичную силу и построим эпюру М₁ (рис. 25):

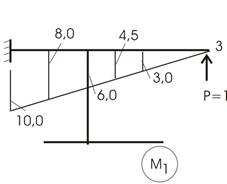
Рис.25

Что составляет погрешность счета:

Не так уж и плохо!

Проверки дают нам основание построить Q_ок по М_ок уже разобранными нами приемами. Процесс построения эпюры Q_ок можно проследить по рисункам 26, 27, где рассмотрены отдельные балки, выделенные из рассчитываемой рамы (консоль не приводится – эпюра Q для нее строится обычным порядком).

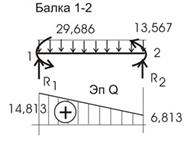
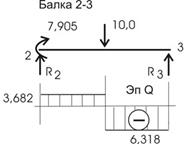
Рис.26

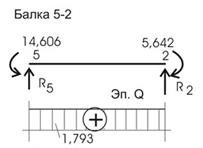
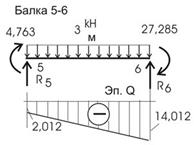
Рис.27

В окончательном виде эпюра перерезывающих сил приведена на рисунке 28.

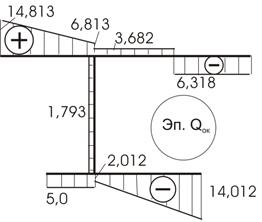
Рис.28

Эпюру N_ок строим по эпюре Q_ок.

Рассматриваем равновесие узла 5 (рис. 29), что позволяет определить продольные усилия в стержнях 5-6 и 5-2.

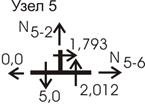
Рис.29

Рассмотрим и равновесие узла 2 (рис. 30), из рассмотрения которого определяются усилия в стержнях 1-2 и 5-2. Следует отметить, что полученные значения продольного усилия в стержне 5-2 при рассмотрении узлов 5 и 2 имеют расхождения в 0,131 (кН). Это нужно отнести на ошибки в наших расчетах.

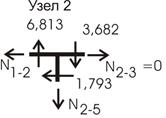
Рис.30

Окончательная эпюра продольных усилий показана на рисунке 31.

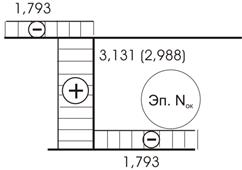
Рис.31

Пример 2.

Требуется для конструкции (рис. 32) определить внутренние усилия (построить эпюры M, Q, N).

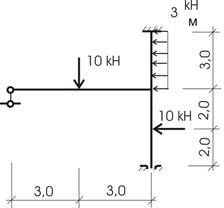
Рис.32

Решение.

Расчет произведем двумя методами: методом перемещений и методом сил (для сравнения).

Расчет рамы методом перемещений

а) Основная система показана на рисунке 33. Одно угловое неизвестное и одно линейное.

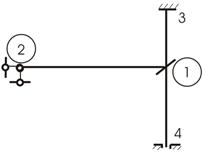
Рис.33

б) Канонические уравнения:

Для вычисления и построим эпюры моментов от перемещений связей (рис. 34) и (рис. 35). Вырезая узел со связью 1 из М₁ и рассмотрев его равновесие, получим:

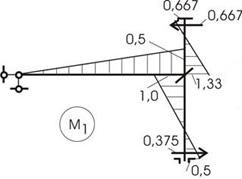
Рис.34

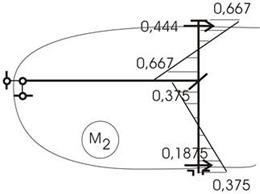
Рис.35

Проведя сечение по опорам из М₂, найдем:

Вырежем узел со связью 1 из М₂, определим

Эпюра М_р приведена на рисунке 36.

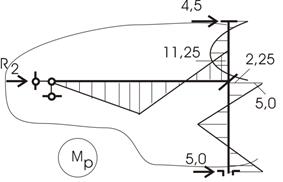
Рис.36

Вырезание узла со связью 1 (рис. 37) позволяет вычислить :

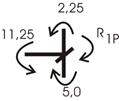
Рис.37

Сечение второй связи и опор рамы дает :

в) Решение системы дает величину перемещений наложенных связей:

г) Эпюру М_ок построим по принципу:

Эпюры и представлены на рисунке 38,а,б.

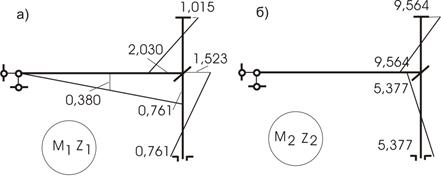
Рис.38

Окончательная эпюра моментов показана на рисунке 39.

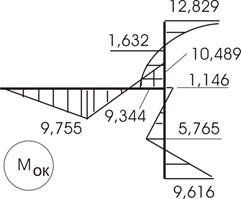
Рис. 39

д) Статическая проверка.

Равновесие узла 1 (рис. 40) удовлетворяет условию равновесия:

10,489 = 10,49.

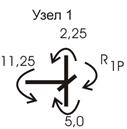
Рис.40

Кинематическая проверка.

Выбираем основную систему метода сил и приложим в опору 2 по вертикали силу P=1. Построим от нее М₁ (рис. 41). Перемножим полученные эпюры и М_ок:

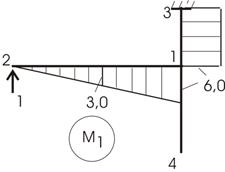
Рис.41

Погрешность составляет:

По эпюре М_ок строим эпюру Q_ок уже разобранными ранее приемами (рис. 42,а), по Q_ок построим эпюру N_ок (рис. 42,б).

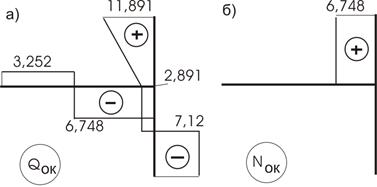
Рис.42

Расчет рамы методом сил

1) Основная система (варианты приводить не будем, рис. 43).

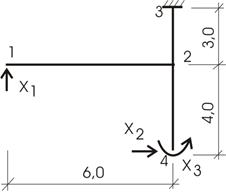
Рис.43

2) Канонические уравнения:

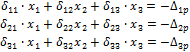
Вычисляем коэффициенты и грузовые слагаемые - . Эпюры моментов от единичных загружений и внешней нагрузки можно видеть на рисунке 44.

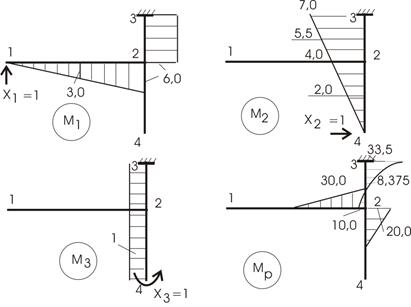
Рис.44

Некоторые вычисления для М_р:

(растянутые левые волокна).

(в обоих последних случаях растянутые правые волокна).

Для применяем правило Верещагина:

Для используем правило Симпсона и Верещагина (для прямолинейных участков):

3) Решение системы уравнений:

дает:

4) Построение М_ок.

Как и прежде (рис. 45).

Сравнение М_ок, вычисленных методом сил и методом перемещений, дает хорошие результаты. Дальнейший ход решения повторяется.

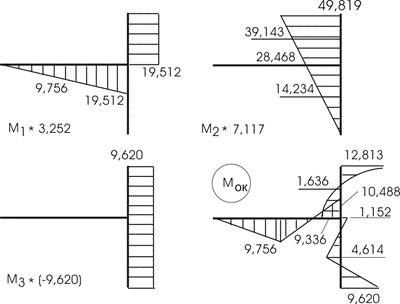
Рис.45

Пример 3.

Для рамы (рис. 46) требуется определить внутренние усилия и построить эпюры M, Q, N.

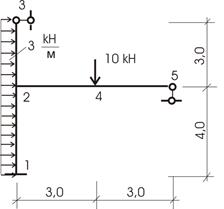
Рис.46

Решение.

1. Определяем число неизвестных:

(подсчет жестких узлов дает единицу).

(степень свободы шарнирной схемы рамы (рис. 47) указывает, что необходимо установить одну связь в узел 2 или в узел 5 по горизонтали).

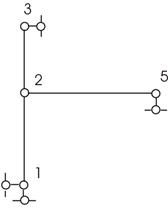
Рис.47

Установим эту связь в узел 5 (рис. 48).

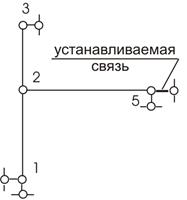
Рис.48

Таким образом, общее число неизвестных n=2.

2. Основная система получается введением в жесткий узел 2 заделки и введением установленной связи в узел 5 (рис. 49).

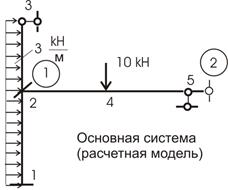
Рис.49

Таким образом, получили раму, у которой ни один узел не имеет возможности перемещаться.

3. Cистема канонических уравнений для полученной основной системы примет вид:

Как было отмечено, их физический смысл заключается в том, что во введенных связях общее (суммарное) реактивное усилие от нагрузки и других воздействий (углового и линейного перемещения) равно нулю.

4. Вычисление реактивных усилий, т. е. коэффициентов при неизвестных и грузовых слагаемых .

а) вычисление коэффициентов

Воздействие углового перемещения на 1 деформированное состояние показано на рисунке 50,а. Используя табличные данные (таблица 1), построим эпюру М₁ (рис. 50,б).

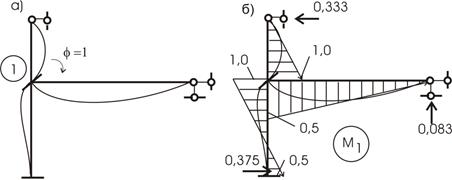
Рис.50

Так, для стержня 1 – 2 (с двух сторон защемленного), где узел 2 поворачивается по часовой стрелке на 1, получаем

Полученные значения заносим на эпюру М₁.

Возникаемое реактивное усилие в связи 1 (жестком узле) найдем вырезанием узла 2 и рассмотрим его равновесие относительно изгибаемых моментов (рис. 51).

Рис.51

В узле действуют 4 изгибающих моментов:

- искомое реактивное усилие, направленное по часовой стрелке (считаем его положительным);

М₂₁ = 1;

М₂₅ = 0,5;

М₂₃ = 1,

тогда

Воздействие линейного смещения на 1 (перемещение 2-ой связи примем влево). Возможная деформация рамы показана на рисунке 52,а. Опять таки, используя табличные данные (таблица 1), строим эпюру М₂ (рис. 52,б, где значения вычислены подстановкой геометрических размеров данной рамы в табличные данные).

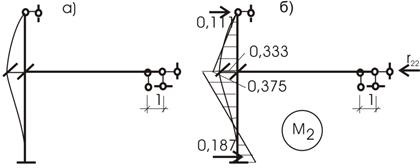
Рис.52

В связи 2 возникает от ее же воздействия реактивное усилие . Проведем сечение, разрезая связь 2 и опорные устройства вертикальных стержней, которые деформируются при воздействии данной связи (рис.52,б). Запишем уравнение статики:

Реактивное усилие считаем положительным, если оно направлено по направлению (влево) перемещения этой связи.

Реактивные усилия . Легче вычислить вырезанием узла 2 (рис. 53) из эпюры М₂ (по аналогии с вырезанием узла 2 из эпюры М₁ – рис. 51).

, т.е. и

Рис.53

Читателям предлагается самостоятельно найти , т. е. реактивное усилие во второй связи от перемещения первой связи.

б) вычисление грузовых слагаемых R_iP

Загружаем раму в основной системе внешней нагрузкой (рис. 49) и, используя табличные данные (таблица 1), строим эпюры для каждого стержня рамы (рис. 54).

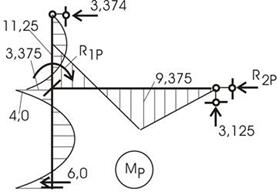
Рис.54

Вырежем узел 2 и рассмотрим его равновесие (рис. 55).

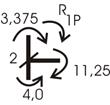
Рис.55

, откуда

Для вычисления воспользуемся сечением, проходящим по связи второй, по опоре 1, по опоре 3 и спроецируем все силы (реакции опор 1, 3) и всю внешнюю нагрузку на ось х, т. е.

, тогда

Теперь можем переходить к решению системы.

5. Решение системы канонических уравнений:

Решение производим одним из способов: подстановкой, исключением неизвестных, способом Крамера и т. д.

Решение дает:

6. Построение окончательной эпюры изгибающих моментов

Воспользуемся принципом независимости действия сил:

Эпюры представлены на рисунке 56.

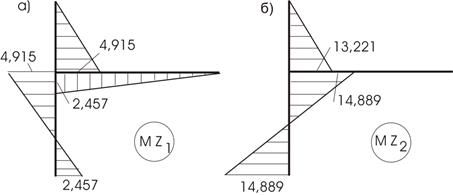
Рис.56

Эпюра представлена на рисунке 57.

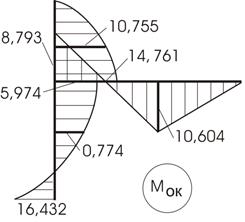
Рис.57

Правильность построения подтверждается проверками: статической и кинематической.

Статическая проверка заключается в равновесии узла 2 (рис. 58).

Такое расхождение допустимо.

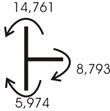
Рис.58

Кинематическая проверка.

Проверим перемещение узла 5 по вертикали – оно должно быть равно нулю, т. к. по этому направлению в этой точке имеется опорный стержень.

Выберем основную систему метода сил и приложим к точке 5 по вертикали единичную силу (рис. 59,а). От этой силы построим эпюру (рис. 59,б).

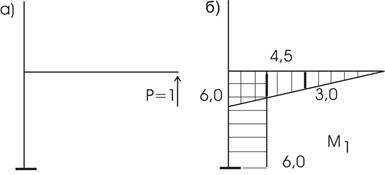
Рис.59

что составляет 0,03%.

Результаты удовлетворяют.

Эпюра Q_ок строится по эпюре М_ок уже рассмотренными нами выше приемами (рис.60,а). Эпюра N_ок строится по эпюре Q_ок (рис. 60,б).

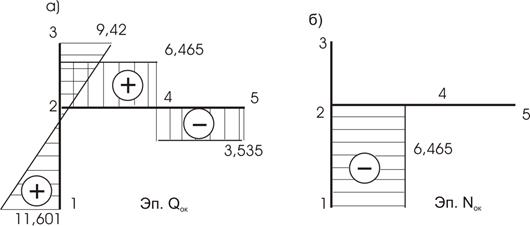
Рис.60

Пример 4.

Рассмотрим трижды статически неопределимую систему (рис. 61,а).

а) Заданная система

б) Основная система

в) Единичное состояние системы

Рис. 61

Решение.

Степень кинематической неопределимости задачи n=1 Неизвестных перемещений – одно. Это поворот узла Каноническое уравнение метода перемещений:

Введём защемление узла. В результате получаем основную систему метода. Реактивный момент в левом защемлении, согласно рис. 61,а, равен:

Превратим теперь защемление в узловое и повернём узел 1 на единичный угол z=1 (рис. 61,в).

Согласно таблице 1 в примыкающих к узлу стержнях на их концах возникают моменты и (рис. 62,б). Из равновесия узла находим:

Подставляя значения найденных коэффициентов в каноническое уравнение (а), получим:

Эпюры от внешней нагрузки в основной системе и от единичного смещения показаны на рис. 62,а,б.

а) б) в)

Рис.62

Используя формулу (а) находим узловые моменты и строим суммарную эпюру моментов (рис. 62,в).

Пример 5.

Рассмотрим два раза статически неопределимую раму (рис. 63,а).

а) Заданная система

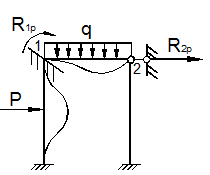
б) Эквивалентная система

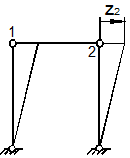
в) Кинематически изменяемая система

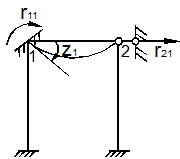
г) Первое единичное состояние

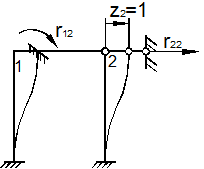
д) Второе единичное состояние

Рис. 63

Решение.

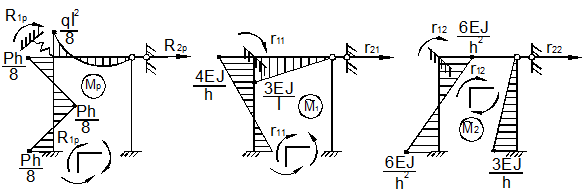
Степень статической неопределимости рамы n=2, ибо она имеет два независимых перемещения узлов: угол поворота узла 1 и линейное перемещение узла 2 (рис. 63,а,б). Соответствующие канонические уравнения метода перемещений имеют вид:

Заданная и эквивалентная системы задачи и единичные состояния изображены на рис.63, г,д. Эпюры моментов от внешней нагрузки в основной системе изображены на рис.64,а. Эпюры моментов от единичных смещений представлены на рис. 64, б,в.

Из условий равновесия узла 1 в каждом из состояний находим:

а) б) в)

Рис. 64

Для определения коэффициентов рассмотрим равновесие отсечённых частей рамы (рис. 65). Из уравнений равновесий находим:

Рис. 65

Канонические уравнения задачи (а) принимают вид

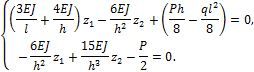
Примем для простоты расчёта l=h и .

Тогда получим:

откуда

Далее по формуле строим эпюру изгибающих моментов (рис. 66).

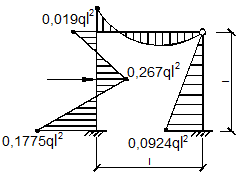
Рис. 66

Пример 6.

Требуется построить методом перемещений эпюры изгибающих моментов М, поперечных сил Q и продольных сил N в раме, показанной на рис. 67.

Рис.67

Решение.

1. В раме один жесткий узел 1, не имеющий линейных перемещений. Поэтому степень кинематической неопределимости равна единице

n = n_y = 1

2. Вводят в узел 1 плавающую заделку: рама превращается в систему стержней с закрепленными концами.

Основная система показана на рис. 68.

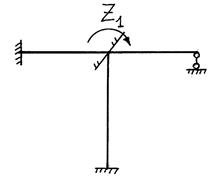
Рис.68

Неизвестный угол поворота Z₁ узла 1 определяют из канонического уравнения

r₁₁ Z₁ + R_1P = 0. (а)

3. В основной системе по таблицам строят эпюру изгибающих моментов М₁ от поворота заделки в узле 1 на угол Z₁ = 1 (рис. 69,б) и эпюру изгибающих моментов от заданной нагрузки М_Р (рис.70). Для построения эпюры М₁ удобно предварительно изобразить картину деформации стержней, возникающую при повороте заделки на угол Z₁ = 1 по часовой стрелке (рис.69,а)

Эпюры М_Р и М₁ строят со стороны растянутых волокон.

а) б)

Рис.69

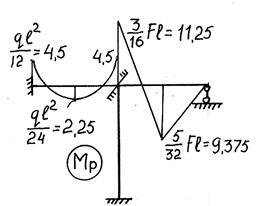
Рис.70

Для записи реакций (реактивных моментов) в заделке при повороте нужно предварительно вычислить значения погонных жесткостей для всех стержней.

Все необходимые выкладки можно сделать непосредственно на эпюре М₁ (рис.69,б).

Для правильного построения эпюры М_Р каждый стержень, на который действует нагрузка, рассматривается отдельно. В ненагруженных стержнях изгиба не возникает.

4. Вычисляют коэффициент r_{11 И} грузовой член R_1P канонического уравнения, рассматривая равновесие узла 1 в эпюрах М_Р и М₁ соответственно. Направление реактивных моментов М_Р и М₁ принимаются положительными при совпадении с направлением поворота узла. Если всегда принимать вначале поворот по часовой стрелке, то направления R_1P и r₁₁ в уравнениях равновесия узла также принимают по часовой стрелке.

Вырезая узел 1 в эпюре М₁ и рассматривая его равновесие (рис.71), получаем

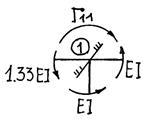
Рис.71

Вырезая узел 1 в эпюре М_Р и рассматривая его равновесие (рис.72), получаем

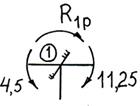
Рис.72

5. Решают уравнение (а), получают действительное значение поворота узла Z₁

6. Строят окончательную эпюру М = М_Р + М₁ Z₁

Предварительно строят так называемую исправленную эпюру М₁Z₁, умножая ординаты эпюры М₁ на найденное значение Z₁.

Указание. Если в расчете угол поворота Z₁ получился со знаком минус, то ординаты исправленной эпюры откладывают с противоположной, чем на эпюре М₁ стороне стержней.

Исправленная эпюра показана на рис. 73.

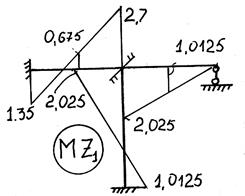
Рис.73

Аккуратно, по точкам складывая эпюры М_Р и М₁Z₁ , получают окончательную эпюру М (рис.74).

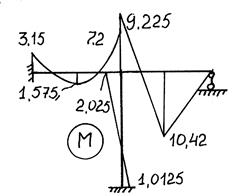
Рис.74

Проверка правильности эпюры М в раме, у которой отсутствуют линейные перемещения узлов, проводится просто: должно быть выполнено равновесие в узле 1. Это условие в решаемой задаче выполняется точно (рис.75).

Указание: Абсолютная ошибка не должна превышать 1%.

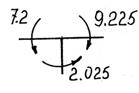
Рис.75

7. Строят эпюру поперечных сил Q.

Предварительно вычисляют поперечные силы на каждом стержне.

Эпюра Q показана на рис. 76.

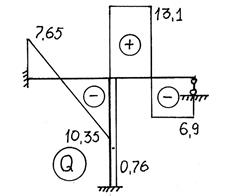
Рис.76

8. Строят эпюру продольных сил N рассматривая равновесие узла 1 (рис.77).

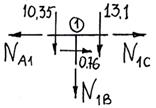
Рис.77

Продольной силой называют проекцию всех левых (или правых) сил, расположенных по левую ( или правую) сторону от сечения, на направление оси стержня. Поэтому можно заключить, что продольная сила в стержне 1С равна нулю.

Напоминание: при рассмотрении равновесия узла следует помнить, что положительные поперечные силы вращают узел по часовой стрелке.

N_1B + 10,35 + 13,1 = 0, N_1B = -23,45.

Эпюра продольных сил показана на рис.78.

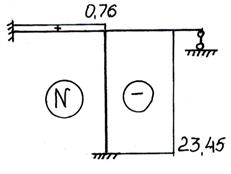
Рис.78

9. Аккуратность вычислений на этапах 7 и 8 проверяют, рассматривая равновесия рамы в целом (рис. 79)

Указание: Абсолютная ошибка не должна превышать 1%.

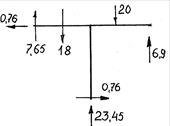
Рис.79

Пример 7.

Требуется построить методом перемещений эпюры М, Q и N в раме, показанной на рис. 80.

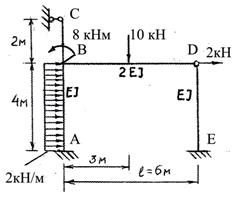
Рис.80

Решение.

1. В раме один жесткий узел (n_у = 1), имеющий одно возможное горизонтальное перемещение этого узла (n_л = 1). Следовательно, рама два раза кинематически неопределима

n = n_у + n_л = 2

2. На рис.81 показана основная система

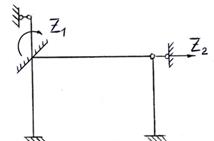
Рис.81

Неизвестные угол поворота узла В (Z₁) и линейное перемещение узла (Z₂) определяют, решая систему канонических уравнений

3. Для вычисления коэффициентов и грузовых членов канонических уравнений строят единичные и грузовую эпюры изгибающих моментов.

Можно избежать ошибок при построении единичных эпюр, если вначале изобразить картину деформаций рамы от единичных перемещений. Предварительно следует вычислить погонные жесткости всех стержней рамы:

Картина деформаций и эпюра изгибающих моментов от поворота заделки в узле В на угол равный единице, построенная по таблицам, показаны на рис.82.

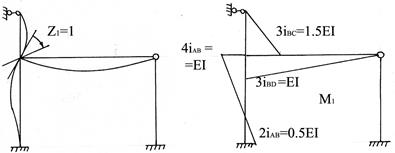
Рис.82

Картина деформаций и эпюра изгибающих моментов от единичного линейного перемещения Z₂ =1, построенная по таблицам, показана на рис. 83.

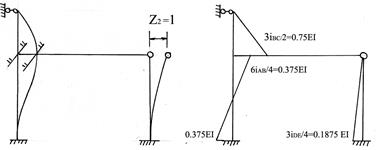
Рис.83

Указание. Удобно следовать договоренности: повороты узлов проводить по часовой стрелке, горизонтальные линейные перемещения – вправо, вертикальные – вверх.

Грузовая эпюра моментов М_Р, построенная по таблицам, показана на рис. 84.

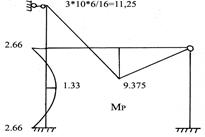
Рис.84

Найдем реакцию (реактивный момент) в заделке узла В от поворота этой заделки на угол Z=1.

Для этого вырежем узел В на эпюре М₁ и рассмотрим равновесие этого узла (рис.85,а)

Из равновесия этого же узла на эпюре М₂ найдем (рис.85,b)

Рис.85

Указание: Направление реакций всегда совпадает с направлениями единичных перемещений.

Чтобы найти реакцию опорной связи поступают следующим образом. Вырезают горизонтальный элемент BD и рассматривают его равновесие (рис.85,с). В уравнение равновесия кроме искомой реакции входят поперечные силы на примыкающих стержнях. Эти поперечные силы находят из таблиц (по абсолютной величине они равны опорным реакциям R). Еще проще эти поперечные силы определяются по формуле Журавского: они равны тангенсам угла наклона единичной эпюры на рассматриваемом участке. Например, на правой стойке поперечная сила равна 0.1875EI/4=0.046875EI и т.д.

Напоминание: Коэффициенты с одинаковыми индексами всегда положительны.

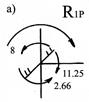
Рис.86

Грузовые члены находят подобным же образом, используя эпюру М_Р. Из рис. 86,а,b следует

Здесь 4 – поперечная сила в узле В на стойке АВ

4. Решая систему канонических уравнений, получают значения

5. Строим окончательную эпюру изгибающих моментов М = М_Р +М₁X₁+М₂X₂.

Предварительно построим так называемые исправленные эпюры, умножив ординаты единичных эпюр на найденные значения неизвестных. Если неизвестное получилось со знаком минус (в рассматриваемом случае – это Z₁),то эпюру строят на противоположном волокне (рис.87).

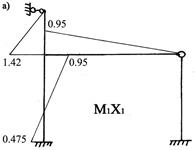
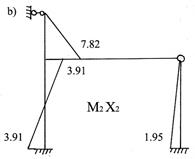
Рис.87

Складывая грузовую эпюру (рис.84) с исправленными (рис.87), получаем окончательную эпюру М. (рис.88).

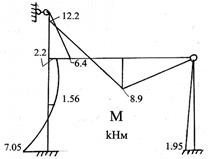
Рис.88

На этом этапе важно проверить равновесие узлов.

Рассмотрим равновесие узла В (нужно не забыть действующий в этом узле момент 8 кНм) (рис.89).

Равновесие соблюдено точно.

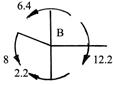
Рис.89

6. Построение эпюры поперечных сил Q.

Вычисляем значения поперечных сил на всех участках рам

Эпюра Q показана на рис.90

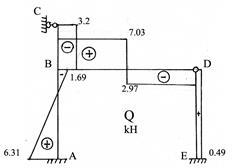
Рис.90

7. Построение эпюры продольных сил N.

Продольные силы определяют из равновесия узлов рамы. Все искомые усилия полагают растягивающими, действующими от узла (рис.91). Поперечные силы списываем с эпюры Q. При этом нужно помнить, что положительные поперечные силы вращают узел по часовой стрелке, а отрицательные – против часовой стрелки. Эпюра N показана на рис. 92.

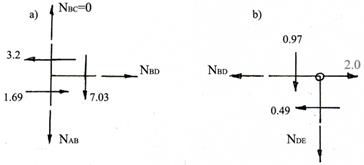
Рис.91

Узел В.

Узел D

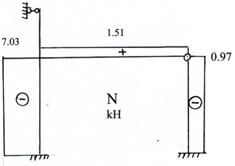
Рис.92

8. Проверка равновесия рамы в целом.

Отрезаем раму от опор и в полученных сечениях прикладываем соответствующие поперечные и продольные силы с эпюр Q и N (рис.93).

Равновесие соблюдается точно.

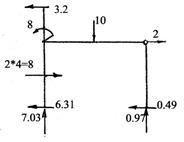
Рис.93

Замечание: Иногда в расчетах не выполняется уравнение равновесия сил в направлении введенной дополнительной опоры, в то время как равновесие моментов в узлах соблюдается. Это может быть связано с ошибками в вычислении коэффициентов и грузовых членов в каноническом уравнении, выражающем равенство нулю реакции в веденной опоре (в рассматриваемом случае – ошибки в вычислении и (или) R_2P).

Вопросы для самопроверки

- Сущность метода перемещений. Определение числа неизвестных метода перемещений.

- В чем состоит основная идея метода перемещений?

- Что понимают под степенью кинематической неопределимости стержневой системы и как она определяется?

- Основная система метода перемещений.

- Каким путем получается основная система в методе перемещений?

- Можно ли построить несколько основных систем метода перемещений при расчете заданной стержневой конструкции?

- Канонические уравнения метода перемещений.

- Каков физический смысл канонических уравнений метода перемещений?

- Как определяется число неизвестных угловых перемещений узлов стержневой системы?

- Чем определяется число линейных перемещений узлов стержневой системы?

- Каков физический смысл системы канонических уравнений метода перемещений?

- Каков физический смысл коэффициентов системы канонических уравнений метода перемещений?

- Что принимают за неизвестные при расчете стержневой системы методом перемещений?

- Как строят единичные и грузовые эпюры изгибающих моментов в основной системе?

- Построение эпюр изгибающих моментов и определение реакций в элементах основной системы метода перемещений (на примере балки защемленной двумя концами).

- Способы определения коэффициентов и свободных членов канонических уравнений метода перемещений.

- Проверка коэффициентов и свободных членов системы канонических уравнений метода перемещений.

- Построение эпюр внутренних усилий в статически неопределимых системах (в методе перемещений).

- Использование симметрии при расчёте рам методом перемещений.

- Расчёт рамы на действие температуры методом перемещений.

- Проверка правильности вычислений единичных и грузовых перемещений.

- Метод перемещений. Степень кинематической неопределимости. Основная система метода перемещений. Лишние неизвестные. Условие эквивалентности исходной задачи и основной системы.

- Этапы решения задач строительной механики методом перемещений.

- Определение степени кинематической неопределимости на примере расчета рам.

- Физический смысл записи канонических уравнений метода перемещений.

- Что означают коэффициенты r_ik, R_ip системы канонических уравнений метода перемещений и как они определяются?

- Построение окончательной эпюры изгибающих моментов при реализации метода перемещений.

- В чем состоит первая обязательная проверка окончательной эпюры изгибающих моментов М?

- Проверка правильности построения эпюр внутренних усилий при решении задач строительной механики методом перемещений.

- Какие проверки правильности расчета в методе перемещений являются основными?

- Где искать ошибку в расчете, если при равновесии моментов в узлах на окончательной эпюре М нет равновесия рамы в целом?

- Сформулируйте допущения, принимаемые при расчете балочных и рамных статически неопределимых систем методом перемещений.

- Какие величины принимаются за неизвестные в расчетах стержневых систем методом перемещений?

- Поясните смысл терминов «узел» системы и «элемент» системы. Определите число узлов и элементов в стержневой системе, заданной преподавателем.

- Каким образом определяется число неизвестных угловых перемещений узлов сооружения? Линейных перемещений узлов сооружения?

- Как определяется степень кинематической неопределимости сооружения?

- Какие требования предъявляются к наложению на узлы сооружения линейных связей при образовании основной системы метода перемещений?

- Задана дважды кинематически неопределимая рамная система, испытывающая силовое воздействие. Требуется:

а) выбрать для нее основную систему метода перемещений;

б) для ее расчета записать в общем виде систему канонических уравнений метода перемещений;

в) пояснить физический смысл каждой строки записанной системы уравнений;

г) пояснить смысл величин r₁₁, r₁₂, r₂₁, r₂₂, R_1F, R_2F, Z₁, Z₂, r₁₁Z₁, r₁₂Z₂, r₂₁Z₁, r₂₂Z₂, входящих в систему уравнений.

- На базе каких данных производится построение эпюр изгибающих моментов в основной системе метода перемещений от единичных кинематических воздействий и от заданной нагрузки?

- Перечислите типы стандартных задач, используемых при расчете стержневых систем методом перемещений. Каким образом они могут быть решены от различного вида кинематических и силовых воздействий?

- Поясните смысл величин, входящих в каноническое уравнение метода перемещений, а также смысл самого уравнения.

- Укажите все промежуточные и окончательные проверки, применяемые в методе перемещений.

- Как используется теорема о взаимности реакций.

- Поясните теорему о взаимности коэффициентов

- Какие способы существуют для вычисления коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений? В чем заключается суть статического способа для их определения? Запишите в общем виде выражение для вычисления коэффициентов r_ii, r_ij, R_iF кинематическим способом.

- Каким образом можно проверить правильность вычисления коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений?

- Как производится построение окончательных эпюр внутренних усилий в заданном сооружении при силовом воздействии на него?

- Сформулируйте смысл статической проверки правильности расчета заданной статически неопределимой системы методом перемещений.

- В какой-то статически неопределимой раме от заданного силового воздействия методом перемещений получена эпюра изгибающих моментов. Как произвести кинематическую проверку ее достоверности?

- Задана конкретная комбинированная система, содержащая незагруженные элементы, ограниченные по концам цилиндрическими шарнирами. Определите степень кинематической неопределимости этой системы с учетом влияния продольных сил упомянутых элементов и осуществите выбор соответствующей основной системы метода перемещений.

- Вспомогательные состояния в методе перемещений. Формирование системы разрешающих уравнений метода перемещений и определение ее коэффициентов. Проверки в методе перемещений.

- Учет наличия бесконечно жестких стержней в рамах при их расчете методом перемещений. Учет симметрии и обратной симметрии при расчете стержневых систем методом перемещений.

- Учет наличия наклонных стержней в раме и упруго оседающих опор при использовании метода перемещений. Расчет неразрезных балок методом перемещений.

- Сформулируйте в общей форме теорему о работе концевых усилий. Какой принцип положен в основу доказательства этой теоремы?

- Задано статически неопределимое сооружение, подверженное независимым друг от друга силовым, температурным и кинематическим воздействиям. Запишите в общем виде в матричной форме систему канонических уравнений метода перемещений для расчета этого сооружения.

- Каким образом в матричной форме вычисляются элементы матрицы внешней жесткости сооружения r?

- Как выбирается основная система при расчете матричным методом перемещений (ММП)?

- Из каких двух напряженных состояний складывается окончательной наряженной состояние заданной стержневой системы?

- Как построить эпюры изгибающих моментов в основной системе от заданной нагрузки?

- Как преобразовать заданную нагрузку к узловой?

- Как сформировать вектор узловой нагрузки?

- Что представляет собой диаграмма положительных моментов?

- Что представляет собой статическая матрица А? Связь между какими величинами она устанавливает?

- Как определяются элементы статической матрицы?

- Что связывает между собой матрица В при расчете рам?

- Как связаны между собой статическая матрица и матрица деформаций?

- На основе какого физического закона устанавливается связь между моментами в расчетных сечениях с деформациями в них?

- Какой вид имеет матрица жесткости для стержня с одним защемленным и другим шарнирно опертым концом?

- Какой вид имеет матрица жесткости для стержня с обоими защемленным концами?

- Как записывается матрица внутренней жесткости для всей системы к?

- Каков физический смысл матрицы внешней жесткости К?

- Каким способом удобно решать матричное уравнение Р = КZ?

- Из какой матричной зависимости находят значения изгибающих моментов в расчетных сечениях от узловой нагрузки?

- Запишите матричное соотношение для вычисления элементов матрицы свободных членов системы канонических уравнений метода перемещений R?

- Запишите развернутую матричную формулу для вычисления матрицы концевых усилий в элементах заданного сооружения: а) в общем случае внешних воздействий; б) в случае силовых воздействий; в) в случае изменения температурного поля; г) в случае кинематических воздействий.

- Как в матричной форме производится проверка правильности расчета заданного сооружения методом перемещений: а) в общем случае внешних воздействий; б) в случае силовых воздействий; в) в случае изменения температурного поля; г) в случае кинематических воздействий.

- Заданная статически неопределимая система (рама или балка) испытывает конкретное температурное или кинематическое (например, в виде смещения опорных связей) воздействие. Определите степень кинематической неопределимости заданного сооружения, выберите основную систему метода перемещений и запишите в общем виде систему канонических уравнений этого метода для расчета на заданное воздействие. Какой смысл имеет i-тая строка системы канонических уравнений? Поясните смысл свободных членов R_it и R_ic этой системы уравнений. Как определяются свободные члены системы канонических уравнений метода перемещений R_it и R_ic?

- Каким образом производится построение эпюры изгибающих моментов _t от заданного температурного воздействия в основной системе метода перемещений? Какие стандартные задачи метода перемещений используются при этом?

- Как определяются линейные перемещения узлов и перекосы элементов в основной системе метода перемещений от равномерных приращений температуры?

- Для заданного сооружения методом перемещений вычислены угловые и линейные перемещения узлов Z₁, Z₂,…, Z_i,…, Z_j,…, Z_n от температурного или кинематического воздействия. Каким образом в нем от этих воздействий определяются внутренние усилия?

- Как производится проверка правильности эпюр внутренних усилий, полученных для заданного сооружения методом перемещений от температурных или кинематических воздействий?

- Почему ординаты эпюр внутренних усилий в статически неопределимых системах при их расчете на температурное или кинематическое воздействие методом перемещений зависят от абсолютных значений жесткостей поперечных сечений элементов сооружения?

- Каким образом может быть построена эпюра изгибающих моментов в основной системе на элементе с прямолинейной осью, защемленном с двух концов, от одновременного поворота угловых связей в разные стороны на угол ? От одновременного поворота угловых связей в одну сторону на такой же угол?

- Какие требования предъявляются к наложению линейных связей на симметрично расположенные узлы стержневых сооружений при выборе основной системы метода перемещений?

- В результате чего происходит упрощение системы канонических уравнений метода перемещений при расчете симметричных стержневых систем на любое внешнее воздействие?

- Какова основная идея метода перемещений?

- Какие величины являются неизвестными в методе перемещений?

- Как определить число неизвестных в методе перемещений?

- Из каких условий выводятся канонические уравнения метода перемещений?

- Как определить коэффициенты канонических уравнений метода перемещений?

- В чем заключается статический способ определения коэффициентов канонических уравнений метода перемещений?

- В чем заключается кинематический способ определения коэффициентов канонических уравнений метода перемещений?

- Запишите канонические уравнения метода перемещений с двумя неизвестными.

- Укажите все промежуточные и окончательные проверки, применяемые в методе перемещений.

- Как используется теорема о взаимности реакций в методе перемещений

- Какие упрощения используются при расчёте симметричных рам методом сил и методом перемещений?

- При каких условиях произойдет разложение системы канонических уравнений метода перемещений, записанной для расчета симметричного стержневого сооружения на любое воздействие (силовое, температурное, кинематическое), на две независимые друг от друга подсистемы уравнений? Какой характер будут иметь неизвестные метода перемещений, входящие в каждую из этих подсистем уравнений?

- Задана симметричная статически неопределимая рама и произвольное внешнее воздействие на нее (силовое, температурное или кинематическое). Определите степень кинематической неопределимости рамы и выберите для ее расчета симметричную основную систему метода перемещений. Какой характер носят неизвестные метода перемещений в полученной основной системе (симметричный, обратно симметричный, несимметричный)? Произведите, при необходимости группировку неизвестных угловых и линейных перемещений симметрично расположенных узлов рамы. Запишите в общем виде систему канонических уравнений метода перемещений для вычисления принятых неизвестных. Какие побочные коэффициенты этой системы уравнений будут равны нулю и почему? Что произойдет с системой канонических уравнений после исключения из нее членов с нулевыми побочными коэффициентами?

- Задана симметричная статически неопределимая рама, подверженная симметричному (обратно симметричному) внешнему силовому, температурному или кинематическому воздействию. Выберите симметричную основную систему метода перемещений; произведите, при необходимости, группировку неизвестных угловых и линейных перемещений симметрично расположенных узлов рамы; запишите в общем виде систему канонических уравнений для расчета рамы на симметричное (обратно симметричное) внешнее воздействие. Укажите, какие неизвестные метода перемещений будут равны нулю при симметричном (обратно симметричном) воздействии? Объясните, почему при указанных внешних воздействиях эти неизвестные равны нулю?

- Перечислите допущения, принимаемые при расчёте рам на устойчивость методом перемещений.

- Выберите основную систему для рам, на рисунке а, б, в. Подсчитайте количество неизвестных метода сил и перемещений.

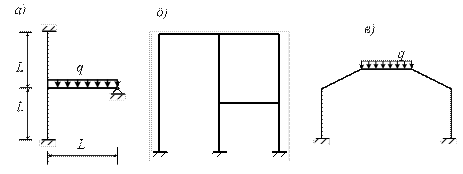
- В чем заключается преимущество группировки неизвестных при расчете симметричных рам?

- В каком случае целесообразно использовать комбинированный метод расчета рам?

- В каком случае целесообразно использовать смешанный метод расчета рам?

- Сформулируйте теорему о взаимности реакций и перемещений.

- Выберите рациональный метод расчета и покажите основную систему для рам, изображенных на рисунке.

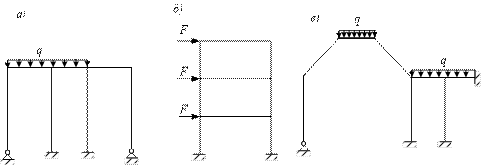
- Определите число основных неизвестных метода перемещений на примерах:

- Определите усилия в раме методом перемещений:

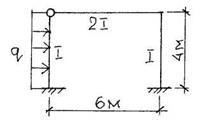
- Определите усилия в раме методом перемещений от неравномерной осадки опор:

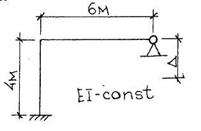
- Определите перемещение точки С по вертикали от воздействия температуры:

- Определите критическую силу методом перемещений для изображенной рамы:

- Перечислите типы опор пространственных систем. Укажите возникающие в них реакции и направления возможных перемещений.

- Определите усилия в стержнях фермы, приведенной на рисунке.

- Разберите порядок расчета рамы, приведенной на рисунке.

- Определите число основных неизвестных метода перемещений для плиты при принятой сетке:

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00