Главная
Лекция 14 (продолжение). Примеры решения на построение эпюр в статически неопределимых системах по методу сил.
Расчет статически
неопределимых рам
Пример 1.
В раме, показанной на рис. 1, требуется определить внутренние усилия и построить ось рамы после деформации. Жесткость всех стержней рамы одинакова и равна EI.

Рис.1
Решение.
Рассматриваемая рама является один раз статически неопределимой и для выбора основной системы требуется отбросить одну лишнюю связь. Такой лишней связью будем считать шарнирно-подвижную опору в точке В. Основная система с отброшенной лишней связью показана на рис. 2.
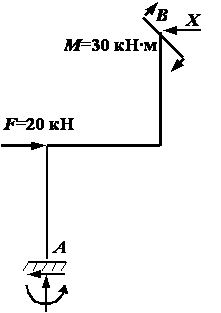
Рис.2
Лишняя
неизвестная, то есть реакция в отброшенной лишней связи, обозначена буквой Х. Условие совместности деформаций для
выбранной основной системы – это условие, приравнивающее нулю горизонтальное
перемещение точки В: ![]() . Это перемещение складывается из перемещения, вызванного
всей заданной нагрузкой
. Это перемещение складывается из перемещения, вызванного
всей заданной нагрузкой ![]() , и перемещения от лишней неизвестной
, и перемещения от лишней неизвестной ![]() . Тогда условие совместности деформаций запишем так:
. Тогда условие совместности деформаций запишем так:
![]() .
.
Будем искать перемещения методом Максвелла – Мора с использованием правила Верещагина. Для этого построим три эпюры изгибающих моментов в основной системе: от заданной нагрузки (рис. 3, а), от единичной силы, соответствующей горизонтальному перемещению в точке В (рис. 3, б), и от лишней неизвестной Х (рис. 3, в).
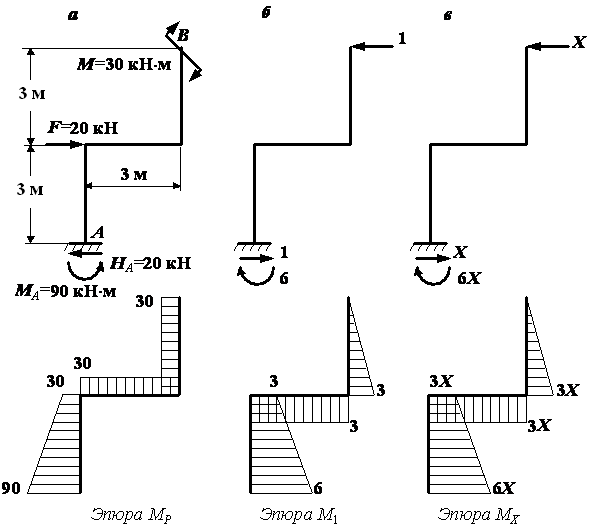
Рис.3
Для
определения ![]() перемножим эпюры МР
и М1:
перемножим эпюры МР
и М1:
![]()
Горизонтальное перемещение точки В от лишней неизвестной Х
![]()
Подставим найденные перемещения в условие совместности деформаций и найдем значение лишней неизвестной:
![]() , откуда
, откуда ![]() кН.
кН.
Строим окончательные эпюры внутренних усилий, приложив к основной системе все нагрузки, включая найденное значение Х (рис. 4).
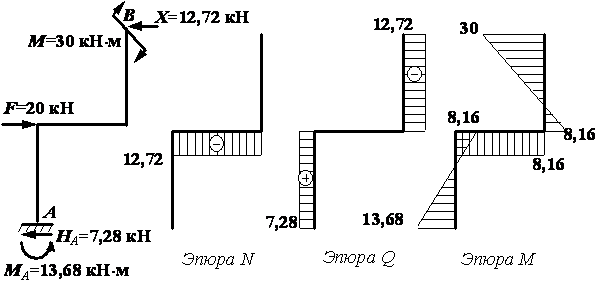
Рис.4
Выполним проверку, перемножив эпюру М с эпюрой М1.
![]()
Изогнутая ось рамы, соответствующая эпюре изгибающих моментов и условиям закрепления показана на рис. 5. Крестиками на рисунке отмечены точки перегиба оси.
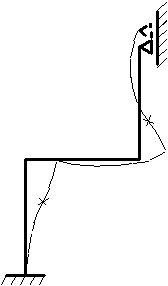
Рис.5
Пример 2.
Построить
эпюры продольных, поперечных сил и изгибающих моментов ![]() ,
, ![]() ,
, ![]() для плоской рамы
(рис.1, а).
для плоской рамы
(рис.1, а).
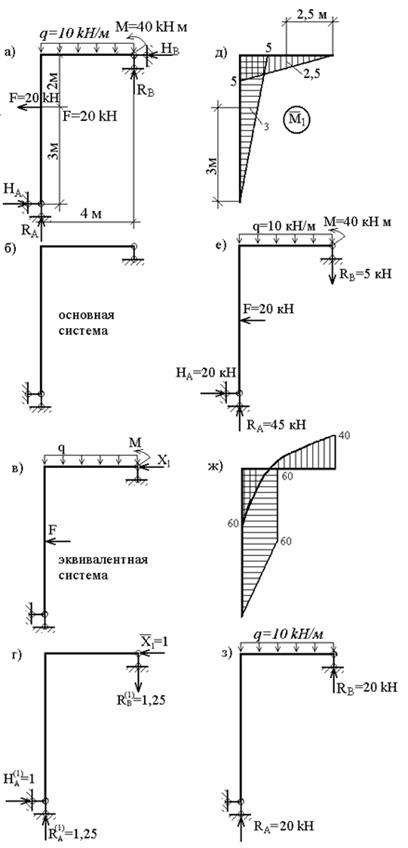
Рис. 1
Решение.
Степень статической неопределимости рамы:
![]()
Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.1, б), т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.1, в).
Заменяя
реакцию лишней связи соответствующей единичной силой, (рис.1, г) строим эпюру моментов ![]() (рис.1, д).
(рис.1, д).
Грузовая эпюра моментов ![]() (рис.1, ж), построенная от одновременного
действия всех внешних нагрузок (рис.1, е),
является знакопеременной на участке, где действует нагрузка
(рис.1, ж), построенная от одновременного
действия всех внешних нагрузок (рис.1, е),
является знакопеременной на участке, где действует нагрузка ![]() . Это создает определенные трудности (хотя и не
непреодолимые!) при ее перемножении с единичной эпюрой
. Это создает определенные трудности (хотя и не
непреодолимые!) при ее перемножении с единичной эпюрой ![]() . В связи с этим целесообразно построить две грузовых
эпюры – отдельно от нагрузки
. В связи с этим целесообразно построить две грузовых
эпюры – отдельно от нагрузки ![]() (эпюра
(эпюра ![]() ) и от совместного действия F и M (эпюра
) и от совместного действия F и M (эпюра ![]() ).
Эти варианты нагружения и эпюры представлены на рис.1,з и рис.2, а,б,в.
).
Эти варианты нагружения и эпюры представлены на рис.1,з и рис.2, а,б,в.
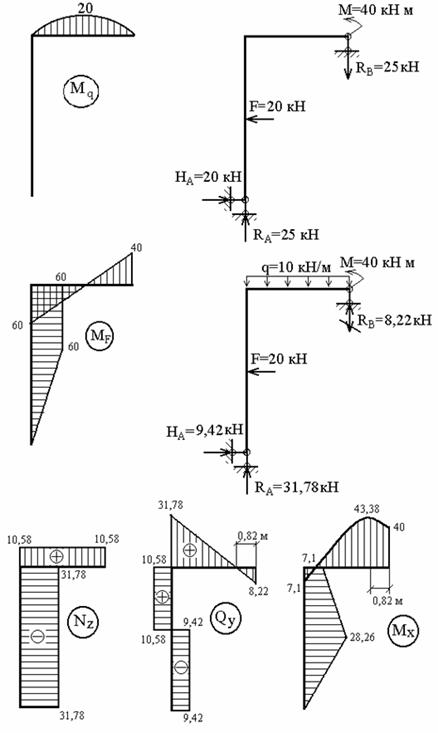
Рис. 2
При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:
![]()
Вычислим коэффициенты канонического уравнения:

Реакция лишних связей:
![]()
Эпюры ![]() ,
, ![]() ,
, ![]() для заданной системы,
загруженной нагрузками F, M, q и X1 (рис.2, г) представлены на рис.2, д,е,ж.
для заданной системы,
загруженной нагрузками F, M, q и X1 (рис.2, г) представлены на рис.2, д,е,ж.
При построении
эпюр ![]() и Q в рамах ординаты можно откладывать в
любую сторону, но обязательно указывать знаки; а при построении эпюр
и Q в рамах ординаты можно откладывать в
любую сторону, но обязательно указывать знаки; а при построении эпюр ![]() знаки можно не
указывать, но обязательно откладывать ординаты со стороны сжатых волокон
соответствующих элементов.
знаки можно не
указывать, но обязательно откладывать ординаты со стороны сжатых волокон
соответствующих элементов.
В обоих рассмотренных примерах универсальная проверка правильности
вычисления коэффициентов канонического уравнения и свободных членов не
выполнялась, так как рама имеют степень статической неопределимости ![]() , а, значит, суммарная единичная эпюра
, а, значит, суммарная единичная эпюра ![]() (если ее построить)
совпадет с единичной эпюрой
(если ее построить)
совпадет с единичной эпюрой ![]() . В этом случае можно (и желательно!) проверить правильность
выполнения расчета при помощи универсальной кинематической проверки
окончательной эпюры моментов
. В этом случае можно (и желательно!) проверить правильность
выполнения расчета при помощи универсальной кинематической проверки
окончательной эпюры моментов ![]() .
.
Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.1, а). Должно выполняться условие:
![]()
Покажем отдельно фрагменты перемножаемых эпюр для ригеля (рис.3,а,б) и стойки (рис.3, в,г) с указанием всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.3, в,г) показана в горизонтальном положении.
Перейдем к рассмотрению более сложной системы – рамы с двумя лишними связями, для которой алгоритм расчета можно реализовать в полном объеме.
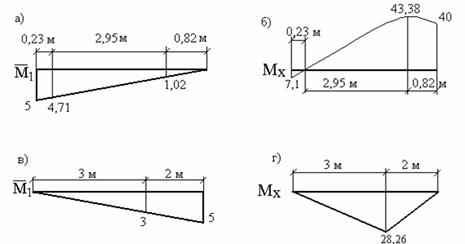
Рис. 3
Пример 3.
Для рамы
(рис.1, а) построить эпюры ![]() ,
, ![]() ,
, ![]() . Выполнить промежуточные и окончательные проверки.
. Выполнить промежуточные и окончательные проверки.
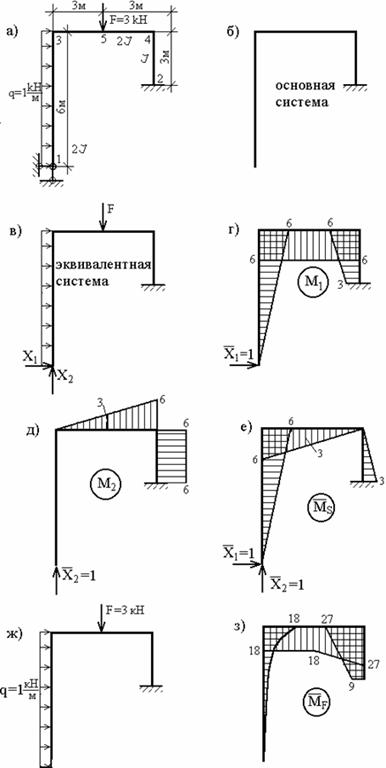
Рис. 1
Решение.
Заданная рама имеет в опорных закреплениях пять связей: две в опоре 1 и три в опоре 2, следовательно, система дважды статически неопределима:
![]()
Основную систему целесообразно выбрать путем удаления шарнирной опоры (рис.1, б). Соответствующая эквивалентная система изображена на рис.1, в.
Система канонических уравнений:
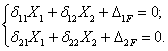
Для вычисления
коэффициентов и свободных членов канонических уравнений строим единичные (![]() ,
, ![]() рис.1, г,д) и грузовую (
рис.1, г,д) и грузовую (![]() , рис.1, ж,з) эпюры
изгибающих моментов, а для выполнения проверок – суммарную единичную эпюру
, рис.1, ж,з) эпюры
изгибающих моментов, а для выполнения проверок – суммарную единичную эпюру ![]() (рис.1, е).
(рис.1, е).
Коэффициенты системы
канонических уравнений вычисляем путем перемножения соответствующих эпюр
по правилу Верещагина. При этом обязательно учитываем разную жесткость
элементов рамы (![]() – на левой
стойке ригеля;
– на левой
стойке ригеля; ![]() – на правой стойке).
– на правой стойке).
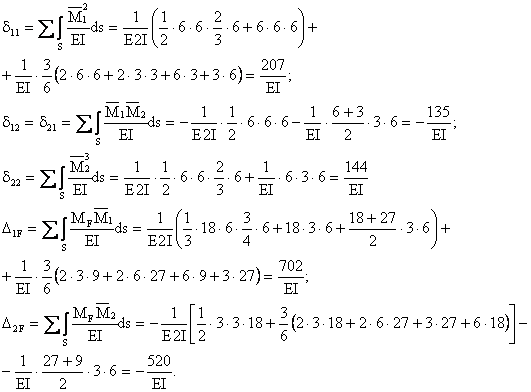
Для проверки
вычисленных коэффициентов при неизвестных и свободных членов канонических
уравнений используем суммарную единичную эпюру ![]() (рис.1, е).
(рис.1, е).
Должны выполняться два условия:
1) ![]()
2) ![]()
Вычисляем
величины ![]() и
и ![]() .
.
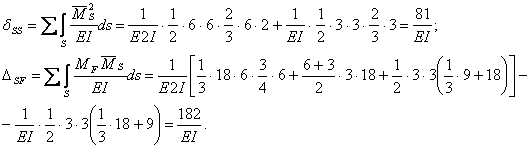
1) ![]()
2) ![]()
таким образом, коэффициенты при неизвестных и свободные члены канонических уравнений вычислены правильно.
Вычисляем
реакции лишних связей:
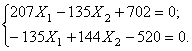
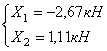
Строим эпюры
продольных (![]() ) и
поперечных (
) и
поперечных (![]() ) сил и
изгибающих моментов (
) сил и
изгибающих моментов (![]() ) для
заданной системы с учетом вычисленных реакций лишних связей (рис.2, а-г).
) для
заданной системы с учетом вычисленных реакций лишних связей (рис.2, а-г).
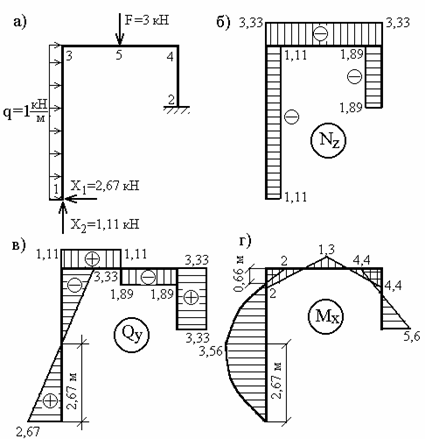
Рис. 2
Для выполнения статической проверки необходимо вырезать жесткие узлы рамы 3 и 4 (рис.2, а) и убедиться в справедливости условий равновесия для каждого из них.
Условия равновесия для узла 3 (рис.3, а):

Условия равновесия для узла 4 (рис.3, б):

Таким образом, статическая проверка выполняется.
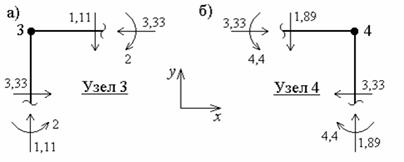
Рис. 3
Для выполнения
кинематической проверки перемножим суммарную единичную эпюру ![]() (рис.1, е) и
окончательную эпюру изгибающих моментов
(рис.1, е) и
окончательную эпюру изгибающих моментов ![]() (рис.2, г):
(рис.2, г):
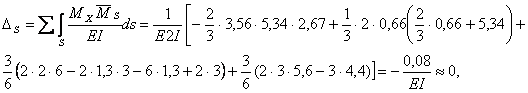
следовательно, все проверки метода сил выполняются, и расчет проделан правильно.
Теперь рассмотрим примеры, иллюстрирующие различные способы использования симметрии.
Пример 6.
Раскрыть статическую неопределимость рамы и построить эпюры N, Q, M (рис. 1).
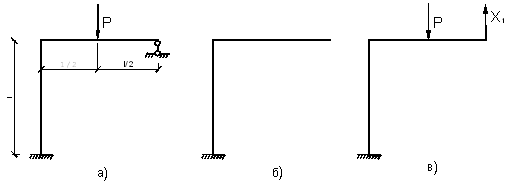
Рис. 1
Заданная
стержневая система (рис.1,а) один раз
статически неопределима ![]() . На рис.1,б
изображена основная система, на рис. 2, в – эквивалентная. Каноническое уравнение метода сил имеет
вид:
. На рис.1,б
изображена основная система, на рис. 2, в – эквивалентная. Каноническое уравнение метода сил имеет
вид:
![]() (1)
(1)
Для
определения коэффициентов ![]() строим эпюры моментов
от единичной силы
строим эпюры моментов
от единичной силы ![]() и внешней силы Р (рис. 2). При определении
и внешней силы Р (рис. 2). При определении ![]() используем эпюру от
единичной силы (рис. 2, а). Она является одновременно эпюрой моментов от
заданной и единичной нагрузки. Применяя формулу Мора при сохранении члена с
изгибающим моментом и способ Верещагина, получаем:
используем эпюру от
единичной силы (рис. 2, а). Она является одновременно эпюрой моментов от
заданной и единичной нагрузки. Применяя формулу Мора при сохранении члена с
изгибающим моментом и способ Верещагина, получаем:
![]()
Для вычисления
![]() воспользуемся формулой
Мора в виде
воспользуемся формулой
Мора в виде
![]()
где
использованы эпюры на рис. 2. Подставляя найденные значения ![]() в каноническое
уравнение, получим:
в каноническое
уравнение, получим:
![]()
откуда находим лишнюю неизвестную:
![]()
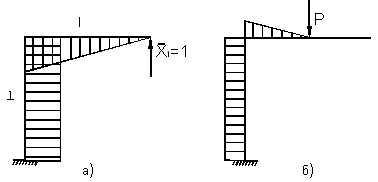
Рис. 2
При построении
эпюр используем эквивалентную систему, в которой Х1 уже известно, и метод сечений. Построение эпюры
моментов можно упростить, если применить способ разложения: эпюру моментов
строить отдельно от внешней нагрузки и силы Х1
, а затем их сложить. Эпюра от внешней нагрузки изображена на рис. 2, б. Эпюру моментов от Х1
получим от единичной силы ![]() (рис. 2, а), если все ординаты этой эпюры умножим
на Х1 (рис. 3, а). Складывая эту эпюру с эпюрой на рис.
2, б получим окончательную эпюру
моментов (рис. 3, б). Эпюры
нормальных и перерезывающих сил строим с использованием метода сечений (см.
рис. 1).
(рис. 2, а), если все ординаты этой эпюры умножим
на Х1 (рис. 3, а). Складывая эту эпюру с эпюрой на рис.
2, б получим окончательную эпюру
моментов (рис. 3, б). Эпюры
нормальных и перерезывающих сил строим с использованием метода сечений (см.
рис. 1).
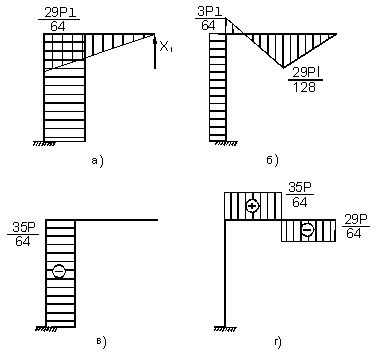
Рис.3
Для
деформационной проверки определим перемещение в направлении силы Х1 эквивалентной системы
(рис. 1). Для этого по правилу Верещагина перемножим окончательную эпюру
изгибающих моментов (рис. 3, б) на
единичную (рис. 2, а) - либо, что всё
равно, эпюры моментов Х1 и
Р (рис. 3,а; рис.2, б) - на
единичную от ![]() .
.
В результате получим:
![]()
что подтверждает правильность полученного решения.
Пример 7.
Рассмотрим два раза статически неопределимую раму (рис. 1, а).
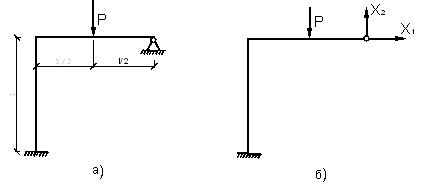
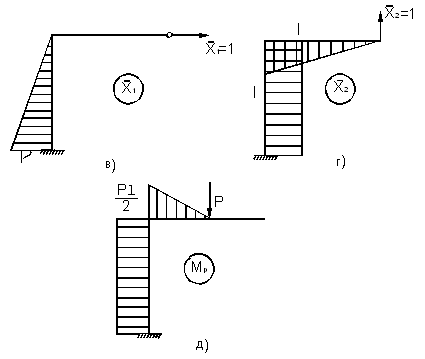
Рис.1
Решение.
На рис. 1, б изображена её эквивалентная система.
Для определения коэффициентов ![]() системы канонических уравнений построим эпюры от единичных
сил и внешней нагрузки (рис. 1, в, г,д). Используя способ Верещагина найдём:
системы канонических уравнений построим эпюры от единичных
сил и внешней нагрузки (рис. 1, в, г,д). Используя способ Верещагина найдём:

Подставляя найденные значения коэффициентов в канонические уравнения для i = 2, получим:
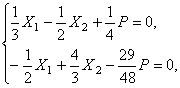
откуда:
![]()
Умножая единичные эпюры на рис. 1 в, г, соответственно на Х1 , Х2 , получим эпюры моментов от этих сил (рис. 2, а,б). Складывая эти эпюры с эпюрой моментов от внешней нагрузки (рис. 1, д), получим суммарную эпюру моментов (рис. 3, а). Эпюры N и Q изображены на рис. 3, б,в соответственно.
Произведём деформационную проверку. Для этого найдём перемещения:
![]()
что подтверждает правильность полученного решения.
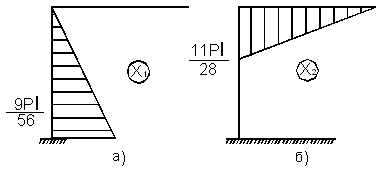
Рис. 2
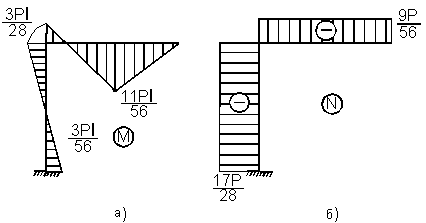

Рис. 3
Пример 8.
Для заданной статически неопределимой рамы (рис.1):
- раскрыть статическую неопределимость методом сил;
- построить эпюры продольных сил, поперечных сил и изгибающего момента;
- выполнить деформационную и статическую проверки.
Дано: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
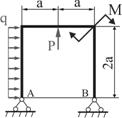
Рис.1
Решение.
Опоры А и В дают
четыре реакции. Для плоской системы сил мы можем составить только три уравнения
равновесия, поэтому заданная расчетная рама является один раз статически
неопределимой. Для построения основной системы нужно устранить одну связь (рис.
2). Для исключения лишней связи заменим неподвижный шарнир в точке В вертикальным стержнем.
Нагружаем основную систему заданной нагрузкой, а вместо отброшенной опоры
прикладываем неизвестную реакцию ![]() .
.
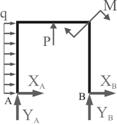
Рис.2
Полное
перемещение точки В основной системы
(от заданной нагрузки и лишнего неизвестного усилия) по направлению удаленной
связи должно быть равно нулю. Полное перемещение ![]() можно представить как сумму перемещений от внешней
(рабочей) нагрузки
можно представить как сумму перемещений от внешней
(рабочей) нагрузки ![]() и неизвестной реакции
и неизвестной реакции ![]() .
.
![]()
Перемещение от
неизвестной реакции ![]() можно представить произведением реакции
можно представить произведением реакции ![]() на перемещение
на перемещение ![]() точки В в направлении действия
точки В в направлении действия ![]() от единичной силы
от единичной силы ![]() . Тогда
. Тогда
![]() .
.
Для
определения перемещений ![]() и
и ![]() рассматриваем основную систему, отдельно нагруженную
заданной нагрузкой (
рассматриваем основную систему, отдельно нагруженную
заданной нагрузкой (![]() ,
, ![]() и
и ![]() ) (рис. 4) и единичной силой
) (рис. 4) и единичной силой ![]() (рис. 5).
(рис. 5).
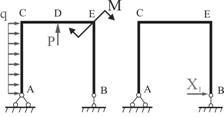
Рис.4 Рис.5
Для нахождения
перемещений применяем способ Верещагина. Для этого необходимо построить эпюры
изгибающих моментов для основной системы, нагруженной рабочей нагрузкой ![]() и единичной силой
и единичной силой ![]() .
.
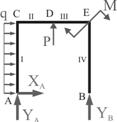
Рис.6
Эпюра![]() . Определяем опорные реакции (рис.6).
. Определяем опорные реакции (рис.6).
![]() ;
; ![]()
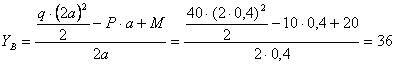 кН
кН
![]() ;
;
![]()
![]() кН
кН
![]() ;
; ![]()
![]() кН
кН
Для проверки
правильности определения реакций опор составим уравнение моментов относительно
точки приложения силы ![]() :
:
![]() ;
;
![]()
![]()
Для построения
эпюры «![]() » будем вычислять величины изгибающих моментов на участках
» будем вычислять величины изгибающих моментов на участках ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Очевидно, что
в точке ![]() :
: ![]() .
.
Очевидно и то,
что в любом сечении стержня ![]() :
: ![]() .
.
Для участка ![]() зависимость
изгибающего момента будет линейной.
зависимость
изгибающего момента будет линейной.
В точке ![]() :
: ![]()
В точке ![]() :
: ![]()
Для участка ![]() зависимость
изгибающего момента также будет линейной.
зависимость
изгибающего момента также будет линейной.
В точке ![]() :
: ![]()
В точке ![]() :
: ![]()
На участке ![]() зависимость
изгибающего момента будет нелинейной.
зависимость
изгибающего момента будет нелинейной.
Для проверки наличия экстремума изгибающего момента определим поперечную силу для границ участка.
![]()
Для точки ![]() :
: ![]()
Для точки ![]() :
: ![]()
Поперечная сила на участке не меняет знак, значит, на эпюре моментов внутри участка не будет экстремума
Выражение
момента на участке ![]()
![]()
Для точки ![]()
![]()
Определим значение момента для середины участка
![]()
Строим эпюру моментов для рабочей нагрузки на сжатых волокнах рамы (рис. 8, а).
Эпюра ![]() . Нагружаем основную систему единичной силой
. Нагружаем основную систему единичной силой ![]() (рис. 7).
(рис. 7).
Определяем реакции опор.
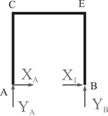
Рис.7
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
На всех участках эпюра единичных моментов будет прямолинейной.
В точке ![]() :
: ![]() .
.
В точке ![]() :
: ![]() .
.
В точке ![]() :
: ![]() .
.
Строим эпюру единичных моментов (рис. 8, б).
Перемещение
точки В от заданной нагрузки ![]() :
:
![]() ,
,
Где ![]() - часть площади эпюры моментов от заданной
нагрузки, для которой легко можно определить площадь и положение центра тяжести
фигуры.
- часть площади эпюры моментов от заданной
нагрузки, для которой легко можно определить площадь и положение центра тяжести
фигуры.
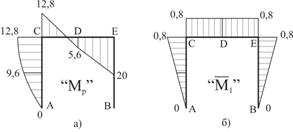
Рис.8
![]() -
ордината эпюры моментов от единичной нагрузки, расположенная под центром
тяжести части площади
-
ордината эпюры моментов от единичной нагрузки, расположенная под центром
тяжести части площади ![]() эпюры
моментов от внешней нагрузки.
эпюры
моментов от внешней нагрузки.
![]() - жесткость рамы.
- жесткость рамы.
Разбиваем площадь эпюры моментов от внешней эпюры на части
На участке ![]() раскладываем площадь эпюры на треугольник
раскладываем площадь эпюры на треугольник ![]() и параболу
и параболу ![]() .
.
Площадь
треугольника ![]()
Центр тяжести
прямоугольного треугольника ![]() находится
на расстоянии одной третей катета от прямого угла
находится
на расстоянии одной третей катета от прямого угла
Площадь
параболы ![]() ,
,
где ![]() - высота
параболы.
- высота
параболы.
Данная
парабола симметрична середине участка ![]() . Там же будет находиться центр тяжести параболы.
. Там же будет находиться центр тяжести параболы.
На участке ![]() рассматриваем площадь эпюры как сумму положительной
площади прямоугольника
рассматриваем площадь эпюры как сумму положительной
площади прямоугольника ![]() и
отрицательной площади треугольника
и
отрицательной площади треугольника ![]() .
.
Площадь
прямоугольника ![]()
Площадь
треугольника ![]()
На участке ![]() раскладываем площадь эпюры на прямоугольник
раскладываем площадь эпюры на прямоугольник ![]() и
треугольник
и
треугольник ![]() .
.
Площадь
прямоугольника ![]()
Площадь
треугольника ![]()
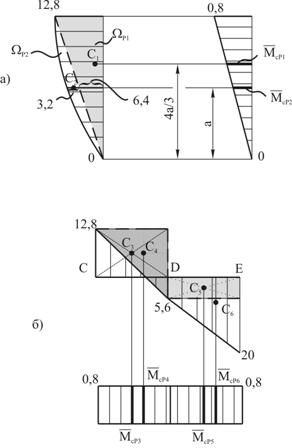
Рис.9
Определяем ординаты эпюры моментов от единичной нагрузки.
![]() ;
;
![]()
![]()
Находим произведение площадей на соответствующие координаты
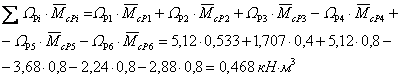
![]()
Если эпюры
моментов от внешней и единичной нагрузки направлены в одну сторону, то
произведение ![]() входит в
уравнение со знаком плюс.
входит в
уравнение со знаком плюс.
Перемещение ![]() получаем аналогичным перемножением эпюры
получаем аналогичным перемножением эпюры ![]() на эпюру
на эпюру ![]()

Полное перемещение
![]()
Откуда
![]()
Таким образом,
реакция отброшенной опоры ![]() .
.
Теперь из уравнений статики легко вычислить остальные реакции для заданной рамы (рис.6)
![]() ;
; ![]()
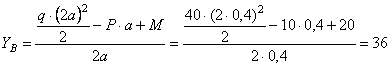 кН
кН
![]() ;
; ![]()
![]() кН
кН
![]() ;
; ![]()
![]() кН
кН
Для проверки
правильности определения реакций опор составим уравнение моментов относительно
точки приложения силы ![]() :
:
![]() ;
;
![]()
![]()
Определяем внутренние силовые факторы на участках
Участок АС
Продольная
сила ![]()
Поперечная
сила ![]()
В точке А ![]()
В точке С ![]()
Поперечная
сила будет равна нулю в сечении с координатой ![]() равной
равной
![]()
Изгибающий
момент ![]()
В точке А ![]()
В точке С ![]()
По середине
участка ![]()
В сечении, для которого поперечная сила равна нулю
![]()
Участок СD
![]()
![]()
![]()
![]()
Участок DЕ
![]()
![]()
![]()
![]()
Участок ВЕ
![]()
![]()
![]()
![]()
Строим эпюру моментов (рис. 10) и выполняем деформационную проверку.
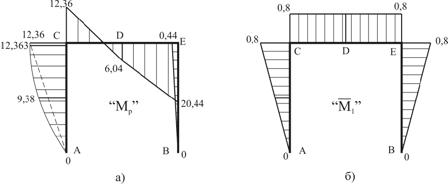
Рис.10

Проверка выполнена.
Строим эпюры продольных сил и поперечных сил (рис. 11).
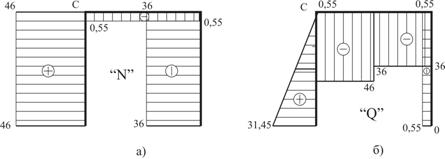
Рис.11
Выполним статическую проверку. Для этого вырезаем узел С и рассматриваем условие равновесия (рис. 12).
Снизу на узел
С действует изгибающий момент ![]() , поперечная
сила
, поперечная
сила ![]() , продольная
сила
, продольная
сила ![]()
Справа
от узла С действует изгибающий момент ![]() , поперечная
сила
, поперечная
сила ![]() , продольная
сила
, продольная
сила ![]()
Рис.12
![]()
![]()
Поперечная
сила ![]() и
поперечная сила
и
поперечная сила ![]() приложены
на бесконечно малом расстоянии от точки С,
поэтому момент от этих сил относительно точки С будет равен нулю. В уравнение моментов в данном случае войдут
только изгибающие моменты.
приложены
на бесконечно малом расстоянии от точки С,
поэтому момент от этих сил относительно точки С будет равен нулю. В уравнение моментов в данном случае войдут
только изгибающие моменты.
![]()
Статическая и деформационная проверки выполнены. Решение статически неопределимой системы правильное.
Пример 9.
Стойки и
ригель стальной рамы (рис. 1) выполнены из одинаковых стержней двутаврового
профиля. Размер l=5 м, интенсивность распределенной
нагрузки q=10 кН/м, допускаемое напряжение ![]() =160 мПа. Подобрать профиль двутавра по условию прочности.
=160 мПа. Подобрать профиль двутавра по условию прочности.

Рис.1
Решение.
Степень статической неопределимости
![]()
Основную систему (рис. 2) получим, убрав «лишнюю» шарнирно – неподвижную опору А.
Каноническое уравнение для заданной рамы имеет вид:
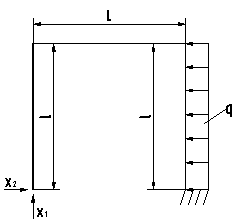
Рис.2
Коэффициенты и свободные члены канонических уравнений определяем по способу Верещагина (перемножение эпюр). Для этого построим две единичные (рис. 3 и рис. 4) и грузовую (рис.5) эпюры моментов.
Коэффициенты
при неизвестных ![]() и грузовые
коэффициенты
и грузовые
коэффициенты![]() определяются
способом Верещагина (рис.3-5):перемножая эпюру
определяются
способом Верещагина (рис.3-5):перемножая эпюру![]() саму на себя
саму на себя

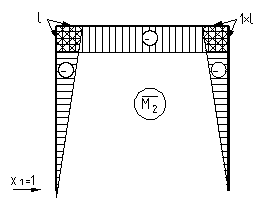
Рис. 3
Рис.
4

Рис. 5
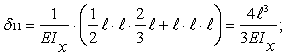
перемножая
эпюры ![]() на
на ![]()

перемножая
эпюры ![]() на
на ![]()
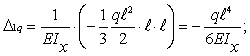
перемножая
эпюры ![]() на
на ![]()
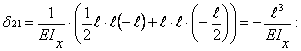
перемножая
эпюру ![]() саму на себя
саму на себя
![]()
перемножая
эпюры ![]() на
на![]()
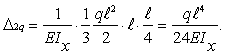
Подставляем найденные значения коэффициентов и грузовых перемещений в канонические уравнения, получаем расчетные уравнения:
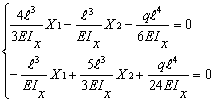
Решая эти уравнения, находим значения X1 и X2.
Для упрощения
расчетов сократим на ![]()

Контрольное уравнение (сумма двух):
![]()
Выражаем Х2 через Х1 из 1-ого уравнения:
![]()
Подставляем во второе;
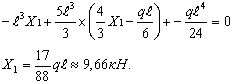
Подставляя в
контрольное уравнение, получим Х2
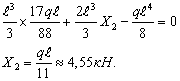
Подставляя
полученные значения Х1и Х2,
как значения неизвестных реакций, в основную систему (рис.2.), построим
эпюры ![]() и
и ![]() для основной системы
(рис.6-8).
для основной системы
(рис.6-8).


Рис. 6 Рис.7
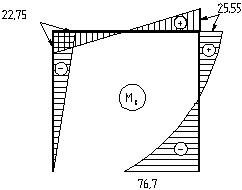
Рис. 8
Опасное сечение в защемлении
![]()
![]()
![]()
Условия прочности по нормальным напряжениям
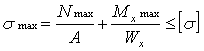
Для прикидки принимаем (по пониженному допускаемому напряжению)
![]()
Для двутавра
№30а (ГОСТ 8239-89): ![]()
![]()
![]()
Проверяем прочность двутавровой рамы №30а по эквивалентным напряжениям в точке поперечного сечения стенки в месте примыкания ее к полке (точка В)
![]()
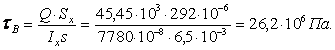
Выполняем проверку прочности рамы в точке В по третьей гипотезе прочности, сложив нормальные напряжения в этой точке от изгиба и растяжения – сжатия

![]()
Окончательно принимаем двутавр №30а.
Пример 10.
1) Раскрыть статическую
неопределимость для заданной рамы (рис.1) и построить эпюры продольных сил ![]() , поперечных сил
, поперечных сил ![]() , и изгибающих моментов
, и изгибающих моментов ![]() .
.
2) выбрать новую основную систему и произвести деформационную проверку.
3) найти полное линейное перемещение сечения А.
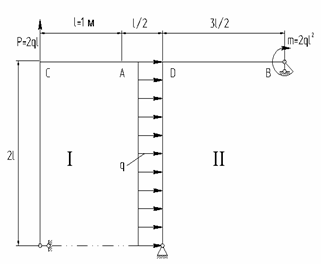
Рис.1
Решение.
Определение неизвестных усилий в статически неопределимой раме можно разбить на следующие этапы:
1. Определение степени статической неопределимости.
2. Выбор основной системы.
3. Построение единичных и грузовых эпюр.
4 Вычисление коэффициентов канонических уравнений метода сил и решение этих уравнений.
5. Построение
эпюр внутренних силовых факторов ![]() ,
, ![]() ,
, ![]() и статическая проверка.
и статическая проверка.
6. Деформационная проверка.
1. Определим степень статической неопределимости системы n=4-3=1. Таким образом, имеем один раз статически неопределимую раму.
2. В качестве основной расчетной системы выбираем раму, представленную на рис.2.
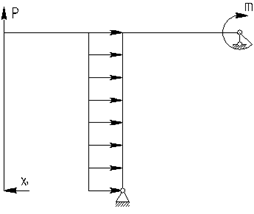
Рис.2
Не следует выбирать систему на рис.3 в качестве основной системы для данной рамы.
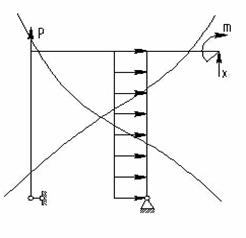
Рис.3.
3.Построение
эпюр М1
и ![]() . Прикладываем в направлении Х1 единичную силу и строим единичную эпюру (рис.4)
. Прикладываем в направлении Х1 единичную силу и строим единичную эпюру (рис.4)
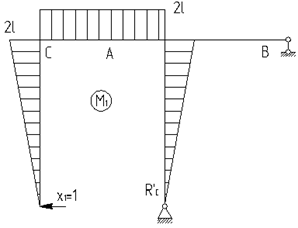
Рис.4
При этом
определяем единичные ![]() в опорах рамы из
уравнений статики:
в опорах рамы из
уравнений статики:
1) ![]() ,
, ![]() ,
, ![]()
2) ![]() ,
, ![]()
3) ![]() ,
, ![]() ,
, ![]()
Переходим к построению
грузовой эпюры ![]() (рис. 5) покажем оси X, Y для рамы при нагрузке
(рис. 5) покажем оси X, Y для рамы при нагрузке ![]() и отброшенной неизвестной силе X1.
и отброшенной неизвестной силе X1.
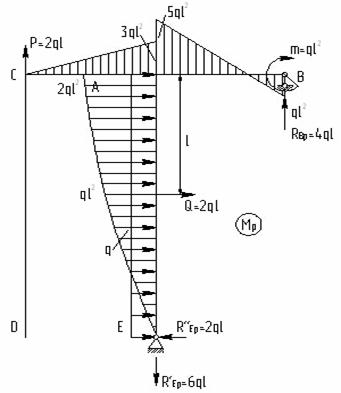
Рис.5
Реакции в опорах при этом определяем из уравнений статики:
1) ![]()
![]()
![]()
![]()
2) ![]()
![]()
3) ![]()
![]()
Выполняем далее проверку равновесия узла D (рис.5).
![]()
Вычисляем
коэффициенты канонического уравнения
![]()
путем “перемножения” эпюр M1 и M2 по правилу Верещагина. Они равны следующим значениям:
![]()
![]()
Далее из канонического уравнения
![]()
находим неизвестную силу X1
![]()
Построение
эпюр ![]() ,
, ![]() ,
, ![]() : Эпюру
: Эпюру ![]() строим, используя
формулу
строим, используя
формулу ![]() .
.
Эпюра ![]() показана на рис.6.
показана на рис.6.

Рис.6
Здесь же выполняем статическую проверку узла D (рис. 7)
Имеем равновесие узла D:
1) ![]()
2) ![]()
3) ![]()
Покажем все
известные нагрузки![]() и найденную силу X1 на схеме
рамы (рис. 7) и определим реакции в опорах.
и найденную силу X1 на схеме
рамы (рис. 7) и определим реакции в опорах.
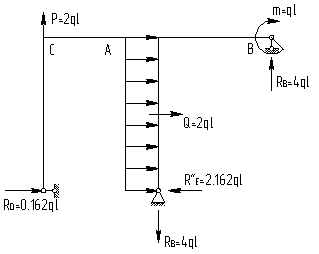
Рис.7
После того как
реакции во всех опорах найдены, строим
эпюры ![]() (рис.8) и
(рис.8) и ![]() (рис.9).
(рис.9).
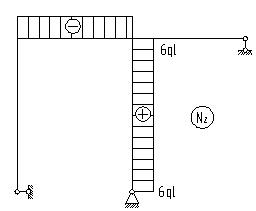
Рис. 8
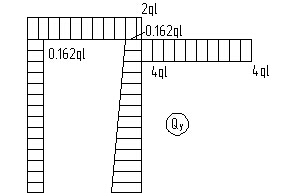
Рис.9
Для проверки
основной системы (рис.10) строим эпюру ![]() для приложенной
единичной силы.
для приложенной
единичной силы.
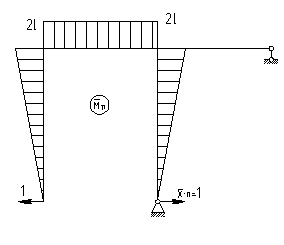
Рис.10
Деформационная проверка этой проверочной ОС имеет вид:

7) Перейдем к определению перемещения сечения А.
При
определении полного перемещения т.А
перекладываем единичные вертикальную и горизонтальную силы в т.А к основной системе. Тогда для
вертикального перемещения строим эпюру ![]() (рис.11)
(рис.11)
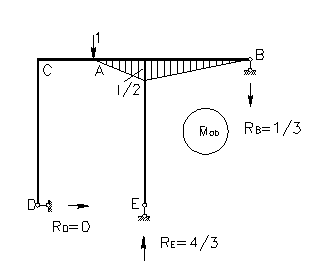
Рис.11
Реакции при этом определяются из уравнения равновесия:
1) ![]() ;
; ![]() ;
; ![]()
2) ![]() ;
; ![]()
3) ![]() ;
;![]() ;
; ![]()
Тогда имеем вертикальное перемещение т. А по формуле:
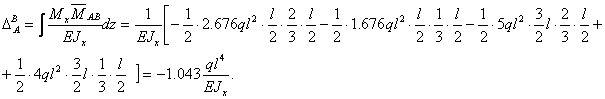
Для
определения горизонтального перемещения т. А
строим эпюру ![]() (рис.12)
(рис.12)

Рис.12
Реакции в опорах также определяем из уравнений равновесия:
1) ![]() ;
; ![]()
2) ![]() ;
; ![]() ;
; ![]()
3) ![]() ;
; ![]() ;
; ![]()
Тогда горизонтальное перемещение равно следующей величине:

Полное перемещение сечения А определяется по формуле:
![]()
Пример 11.
Решить плоскую раму, представленную на рисунке.
Данная рама дважды статически неопределима. На рисунке показаны три из большого числа возможных эквивалентных систем. Остановимся на первой системе и запишем для нее канонические уравнения

Коэффициенты этих уравнений вычислим способом Верещагина. Для этого построим эпюры изгибающих моментов от распределенной нагрузки и единичных сил. Перемножая эпюры согласно индексам коэффициентов, находим
![]()
Подставляя эти значения коэффициентов в канонические уравнения и решая их, получаем
![]() .
.
Суммируя
ординаты эпюры «P» с ординатами эпюры
«1», умноженными на X1, и эпюры «2», увеличенными в ![]() раз, строим суммарную эпюру изгибающих
моментов
раз, строим суммарную эпюру изгибающих
моментов ![]() .
.
Изгибающий момент в текущем сечении горизонтального участка находим по формуле:
![]() .
.
Приравнивая
нулю производную ![]() ,
устанавливаем, что эта функция имеет экстремум при
,
устанавливаем, что эта функция имеет экстремум при ![]() , причем
, причем ![]() .
.
Пример 12.
Построить эпюру изгибающих моментов для рамы, представленной на рисунке.

Рама один раз
статически неопределима. Выберем основную систему, удаляя одну связь в нижнем
(или верхнем) шарнире. Однако в рассматриваемой раме горизонтальные и вертикальные
опорные связи неравноценны. Если удалить горизонтальную
связь, то при любой нагрузке реакция ![]() оставшейся
вертикальной вязи должна быть бесконечно большой, так как линия ее действия
проходит через центр верхнего шарнира, а момент внешней нагрузки относительно
этого шарнира не равен нулю. Чтобы воспринять даже самую малую нагрузку,
эта рама должна сначала повернуться как жесткое целое (без деформации) на
бесконечно малый угол
оставшейся
вертикальной вязи должна быть бесконечно большой, так как линия ее действия
проходит через центр верхнего шарнира, а момент внешней нагрузки относительно
этого шарнира не равен нулю. Чтобы воспринять даже самую малую нагрузку,
эта рама должна сначала повернуться как жесткое целое (без деформации) на
бесконечно малый угол ![]() . Тогда плечо реакции
. Тогда плечо реакции ![]() станет отличным от
нуля, а сама реакция будет конечной, но значительной по величине.
станет отличным от
нуля, а сама реакция будет конечной, но значительной по величине.
Такая система является мгновенно геометрически изменяемой. Ее в качестве основной системы выбирать нельзя.
Положение сразу же изменяется, если удалить не горизонтальную, а вертикальную опорную связь. В такой основной системе при любой нагрузке опорные реакции и внутренние силовые факторы будут конечными и определенными. Эквивалентная система, соответствующая этой основной системе, представлена на рисунке. Там же приведены эпюры изгибающих моментов от заданной и единичных нагрузок.
Вычисляя
коэффициенты канонического уравнения ![]() интегрированием на
криволинейных участках и перемножением эпюр на
прямолинейных, получаем
интегрированием на
криволинейных участках и перемножением эпюр на
прямолинейных, получаем

Отсюда
![]() .
.
Суммарный изгибающий момент на криволинейном участке изменяется по закону
![]() .
.
Приравнивая
нулю производную от ![]() :
:
![]() ,
,
получаем
![]() .
.
Следовательно,
при ![]() функция
функция ![]() имеет экстремум,
причем
имеет экстремум,
причем ![]() . Суммарная эпюра приведена на рисунке.
. Суммарная эпюра приведена на рисунке.
Пример 13.
Решить раму, представленную на рисунке.
Если не использовать свойств симметричных систем, то для раскрытия статической неопределимости потребовалось бы решать систему из шести линейных алгебраических уравнений. Использование свойств симметрии упрощает решение задачи. Один из стержней рамы совпадает с вертикальной осью симметрии. Поэтому основную систему выберем разрезом боковых стержней рамы по горизонтальной оси симметрии. Чтобы эквивалентная система была симметричной, внешние силы P отнесем равными частями к обеим сторонам разреза.
В силу симметрии рамы относительно вертикальной оси силовые факторы в проведенных сечениях равны по величине и противоположны по направлению, а вследствие симметрии относительно горизонтальной оси перерезывающие силы в этих сечениях равны нулю. Система канонических уравнений имеет вид

Перемножая эпюры (см. рис.), находим коэффициенты этой системы
![]() .
.
Решение
канонических уравнений дает ![]() ,
, ![]() . Суммарная эпюра приведена на рисунке.
. Суммарная эпюра приведена на рисунке.
Пример 14.
Рассмотрим теперь обратно симметричные стержневые системы.
Геометрически симметричные стержневые системы с нагрузкой, обратно симметричной относительно оси (плоскости) симметрии системы, называются обратно симметричными, или косо симметричными.
Перемещения симметричных сечений такой системы и одноименные внутренние силовые факторы в них равны по величине и обратно симметричны по направлению. В сечении на оси симметрии симметричные силовые факторы всегда равны нулю, так как они вызывают симметричные деформации, не соответствующие характеру деформаций от заданной нагрузки.
Подтвердим изложенное на примере плоской обратно симметричной рамы (см. рис.). Выберем основную систему разрезом рамы по оси симметрии и построим эпюры изгибающих моментов от заданных нагрузок и единичных усилий, приложенных вместо искомых силовых факторов (см. рис.).
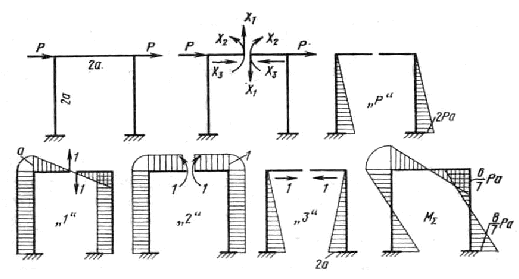
Составим канонические уравнения
Вычислим коэффициенты этой системы способом Верещагина.
Так как произведение
симметричной эпюры на обратно-симметричную равно нулю, то ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Итак, система канонических уравнений распадается на две группы
![]()
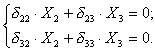
Вторая группа представляет собой систему линейных однородных уравнений, определитель которой отличен от нуля. Отсюда следует, что нормальная сила X2 и изгибающий момент X3 в сечении по оси симметрии рамы равны нулю.
Итак, подтверждено, что в сечении по оси симметрии обратно симметричной стержневой системы симметричные силовые факторы - изгибающие моменты и нормальные силы равны нулю и могут действовать только обратно симметричные силовые факторы. А это означает, что в симметричных сечениях (в том числе и опорных) обратно симметричных стержневых систем силовые факторы равны по величине и обратно симметричны по направлению.
Использование в расчетах отмеченных свойств обратно симметричных систем позволяет существенно упростить решение задачи.
Для рассматриваемой на рисунке задачи коэффициенты канонического уравнения будут:
![]()
Таким образом ![]() .
.
Суммарная эпюра изгибающих моментов имеет обратно симметричный вид (см. рис. ).
Пример 16.
Раскрыть статическую неопределимость рамы, представленной на рисунке.
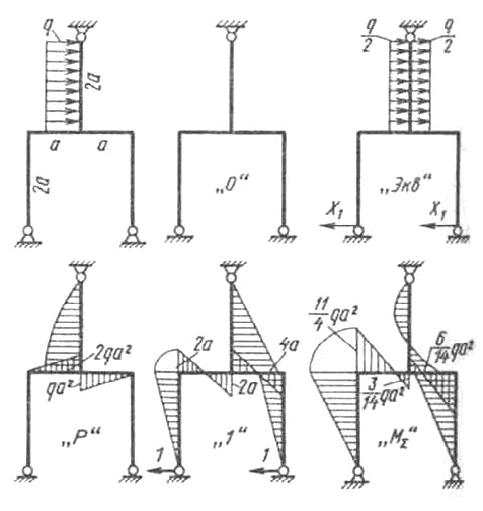
Данная рама обратно симметрична. В этом нетрудно убедиться, представив распределенную нагрузку так, как показано на рисунке. Основную систему получим, сняв горизонтальные связи в нижних шарнирных опорах. В данном случае в качестве основной выбрана, вообще говоря, статически неопределимая система. Однако при обратно симметричной нагрузке опорные реакции в катковых опорах будут равны по величине и противоположны по направлению и их можно определить из уравнения равновесия.
Коэффициенты
канонического уравнения ![]() найдем перемножением
эпюр:
найдем перемножением
эпюр:
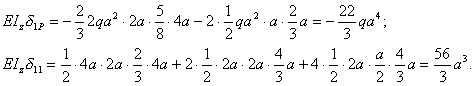
Тогда ![]() .
.
Суммарная эпюра представлена на рисунке.
Пример 19.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к =2; l = 9 м, h = 5 м, q = 10 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
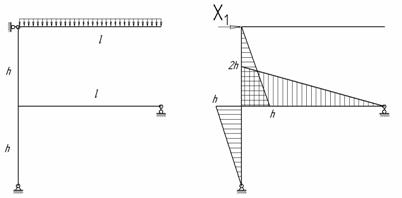
Рис.1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая
эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая
эпюра M) (рис.3).
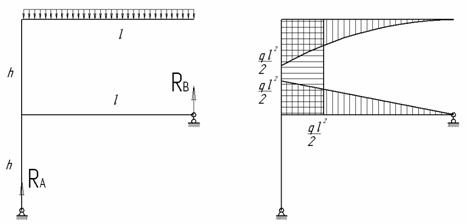
Рис.2
Рис.3
4. Для
отыскания коэффициентов канонического уравнения ![]() и
и ![]() используем способ
Верещагина.
используем способ
Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:

Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:
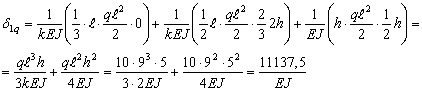
5. Из канонического уравнения найдем неизвестную Х1:
![]()
6. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4).
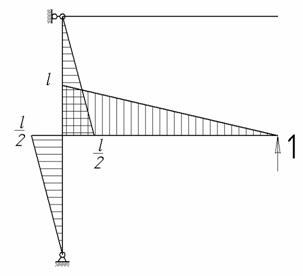
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
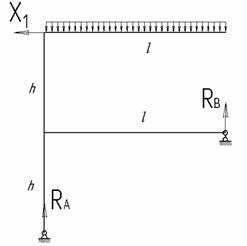
Рис.5
Из уравнений статики определяем опорные реакции:

Составляем выражения для N, Qy и Мx по участкам и строим эпюры N, Q, M (рис.6 и рис.7).
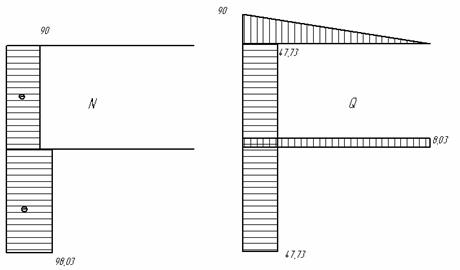
Рис.6
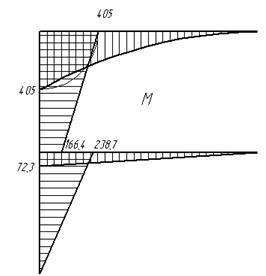
Рис.7
Пример 20.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к = 1,9; l = 4 м, h = 5 м, q = 6 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
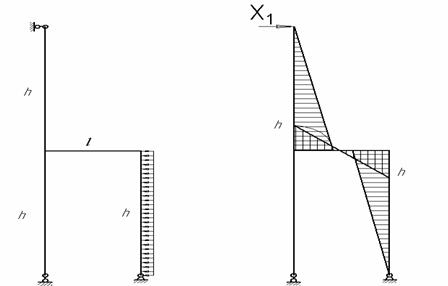
Рис.1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
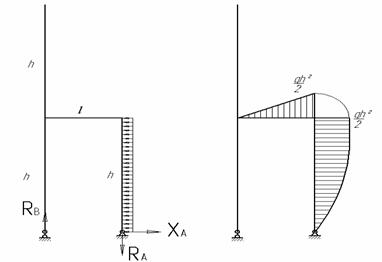
Рис.2
Рис.3
4. Для
отыскания коэффициентов канонического уравнения ![]() и
и ![]() используем способ Верещагина.
используем способ Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:
![]()
Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:

5. Из канонического уравнения найдем неизвестную Х1:
![]()
6. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4).
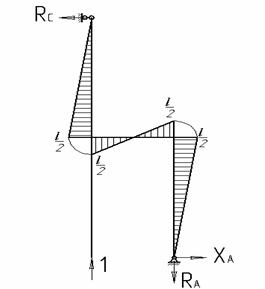
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
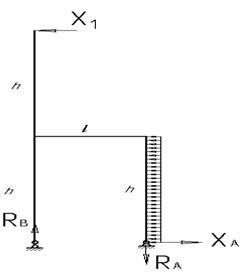
Рис.5
Из уравнений статики определяем опорные реакции:
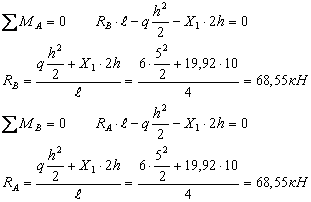
Составляем выражения для N, Qy и Мx по участкам. и строим эпюры N, Q, M (рис.6,7,8).
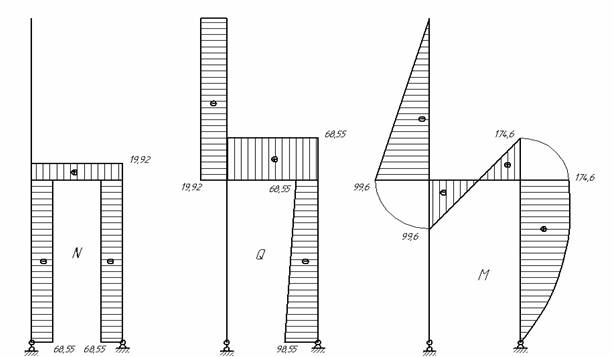
Рис.6
Рис.7
Рис.8
Пример 21.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к = 1,9; l = 10 м, h = 6 м, q = 4 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
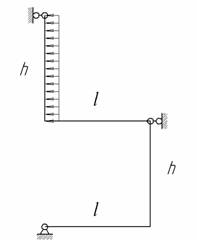
Рис.1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
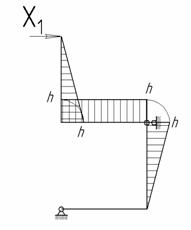
Рис.2
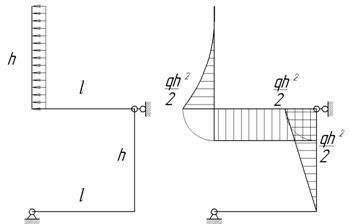
Рис.3
4. Для
отыскания коэффициентов канонического уравнения ![]() и
и ![]() используем способ
Верещагина.
используем способ
Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:
![]()
Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:

5. Из канонического уравнения найдем неизвестную Х1:
![]()
6. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4).
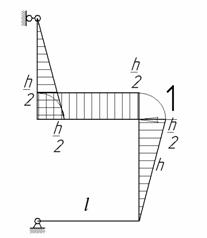
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
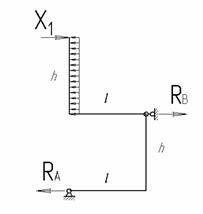
Рис.5
Из уравнений статики определяем опорные реакции:

Составляем выражения для N, Qy и Мx по участкам и строим эпюры N, Q, M (рис.6 и рис.7).
Рис.6
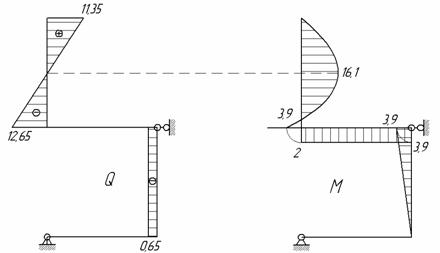
Рис.7
Пример 22.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к = 1,9; l = 9 м, h = 5 м, q =6 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
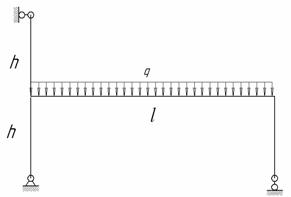
Рис.1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
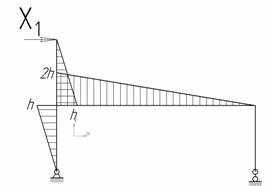
Рис.2
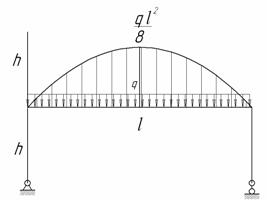
Рис.3
4. Для
отыскания коэффициентов канонического уравнения ![]() и
и ![]() используем способ
Верещагина.
используем способ
Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:

Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:
![]()
5. Из канонического уравнения найдем неизвестную Х1:
![]()
6. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4).
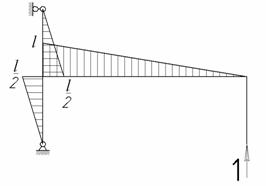
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
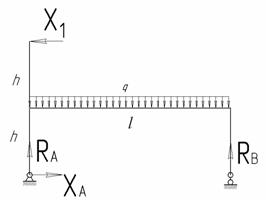
Рис.5
Из уравнений статики определяем опорные реакции:
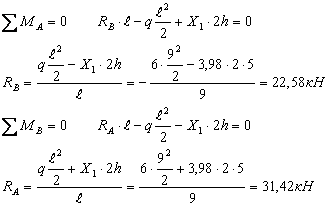
Составляем выражения для N, Qy и Мx по участкам и строим эпюры N, Q, M (рис.6 и рис.7).
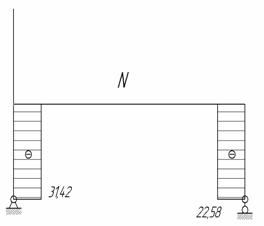
Рис.6
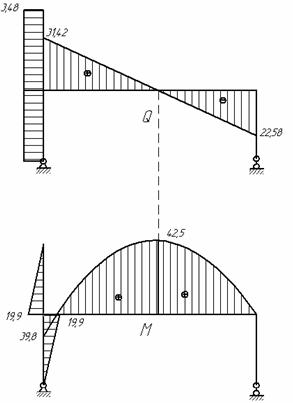
Рис.7
Пример 23.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к = 1,9; l = 11 м, h = 2 м, q =15 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
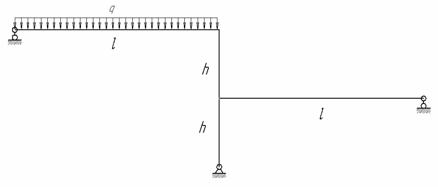
Рис.1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
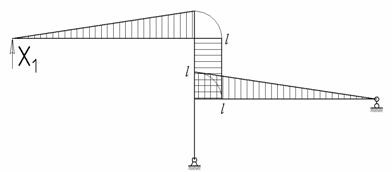
Рис.2
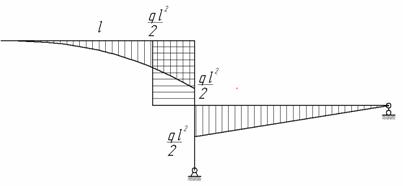
Рис.3
4. Для отыскания
коэффициентов канонического уравнения ![]() и
и ![]() используем способ
Верещагина.
используем способ
Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:
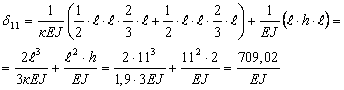
Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:

5. Из канонического уравнения найдем неизвестную Х1:
![]()
5. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4).
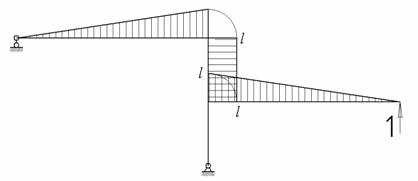
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
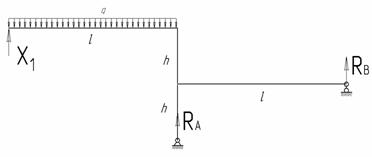
Рис.5
Из уравнений статики определяем опорные реакции:

Составляем выражения для N, Qy и Мx по участкам и строим эпюры N, Q, M (рис.6 и рис.7).
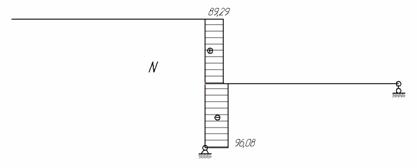
Рис.6
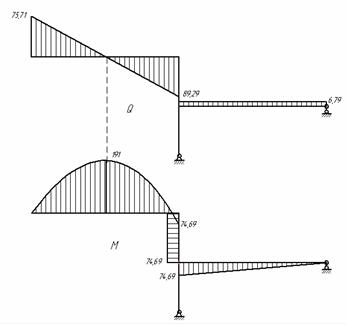
Рис.7
Пример 24.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к = 1,9; l = 4 м, h = 5 м, q = 4 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
Рис.1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
Рис.2
Рис.3
4. Для
отыскания коэффициентов канонического уравнения ![]() и
и ![]() используем способ
Верещагина.
используем способ
Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:

Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:

5. Из канонического уравнения найдем неизвестную Х1:
![]()
6. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4)..
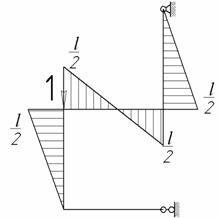
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
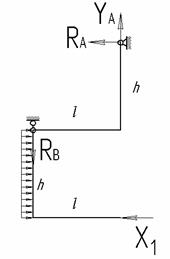
Рис.5
Из уравнений статики определяем опорные реакции:
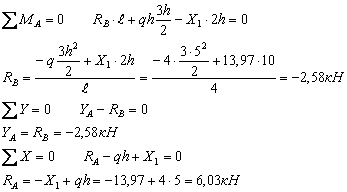
Составляем выражения для N, Qy и Мx по участкам и строим эпюры N, Q, M (рис.6 и рис.7).
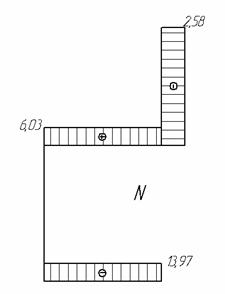
Рис.6
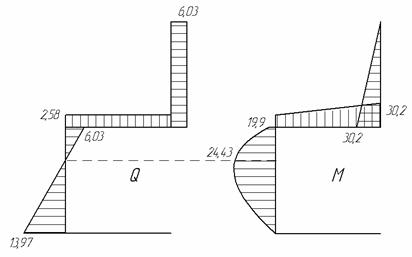
Рис.7
Пример 25.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к = 1,4; l = 6 м, h = 2 м, q = 15 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
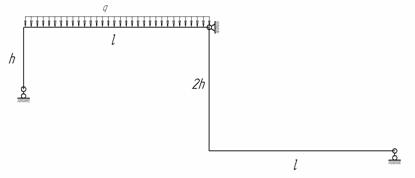
Рис. 1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
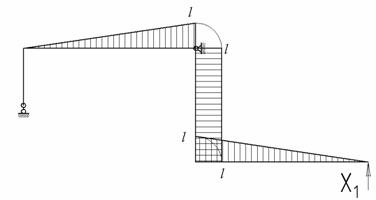
Рис.2
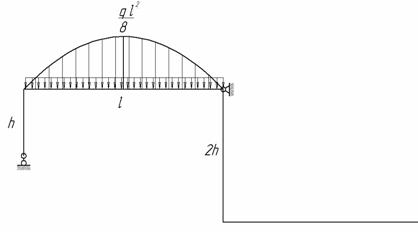
Рис.3
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
4. Для
отыскания коэффициентов канонического уравнения ![]() и
и ![]() используем способ
Верещагина.
используем способ
Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:
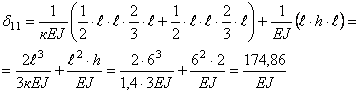
Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:
![]()
5. Из канонического уравнения найдем неизвестную Х1:
![]()
6. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4).
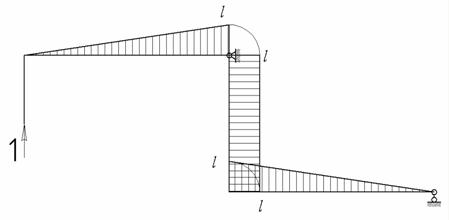
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
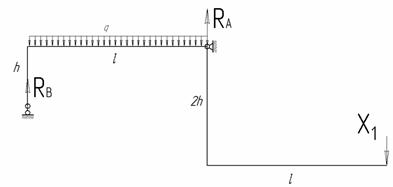
Рис.5
Из уравнений статики определяем опорные реакции:

Составляем выражения для N, Qy и Мx по участкам и строим эпюры N, Q, M (рис.6 и рис.7).
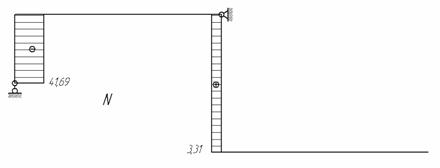
Рис.6
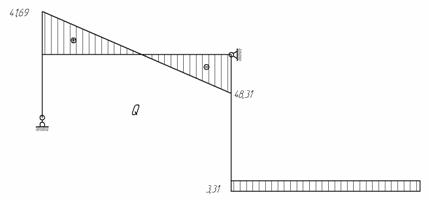
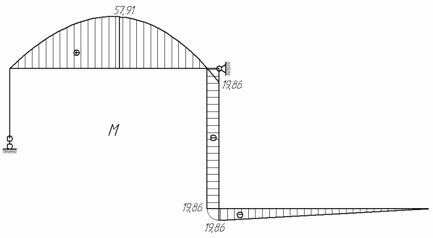
Рис.7
Пример 26.
Для изображенной на рис.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J, а горизонтальные элементы – кJ; к = 1,3; l = 11 м, h = 3 м, q =15 кН/м требуется:
1. установить степень статической неопределимости и выбрать основную систему;
2. написать канонические уравнения;
3. построить эпюры изгибающего момента от единичных сил и от заданной нагрузки;
4. найти коэффициенты канонических уравнений;
5. найти величины «лишних» неизвестных Х;
6. выполнить деформационную проверку правильности определения неизвестных;
7. построить окончательные эпюры внутренних силовых факторов N, Qy, Mx.
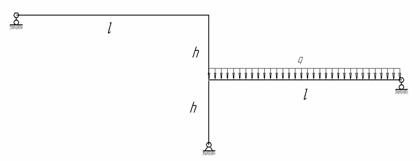
Рис. 1
Решение.
1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае s = 4 – 3 = 1.
Для раскрытия статической неопределимости используем метод сил.
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() (1)
(1)
Здесь ![]() - перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
- перемещение
точки А в направлении силы Х1
от действия силы X1= 1;
![]() - перемещение
точки А в направлении силы Х1
от действия нагрузки q.
- перемещение
точки А в направлении силы Х1
от действия нагрузки q.
3. Строим
эпюры изгибающего момента ![]() отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
отдельно от действия
силы X1 = 1 (рис.2) и нагрузки q (грузовая эпюра M) (рис.3).
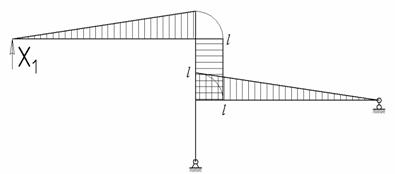
Рис.2
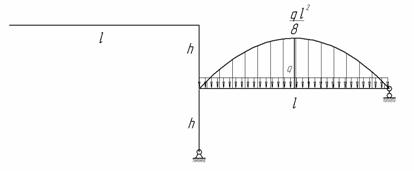
Рис.3
4. Для
отыскания коэффициентов канонического уравнения ![]() и
и ![]() используем способ
Верещагина.
используем способ
Верещагина.
Для
определения коэффициента ![]() единичную эпюру
единичную эпюру ![]() умножаем саму на себя:
умножаем саму на себя:
Для
определения коэффициента ![]() умножаем единичную
эпюру
умножаем единичную
эпюру ![]() на грузовую эпюру М:
на грузовую эпюру М:
![]()
5. Из канонического уравнения найдем неизвестную Х1:
![]()
6. Выполним деформационную проверку правильности нахождения силы Х1 (рис.4).
Рис.4

что подтверждает правильность решения.
7. Убедившись в правильности определения силы Х1, можно приступать к построению окончательных эпюр продольных, поперечных сил и изгибающих моментов. Следует отметить, что если неизвестная сила Х1 получилась отрицательной, направление этой силы прежде, чем строить эпюры, следует поменять на противоположное, а знак минус убрать (рис.5).
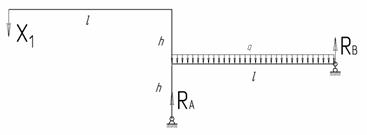
Рис.5
Из уравнений статики определяем опорные реакции:
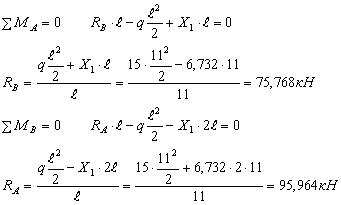
Составляем выражения для N, Qy и Мx по участкам и строим эпюры N, Q, M (рис.6 и рис.7)
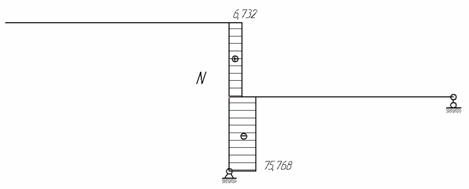
Рис.6
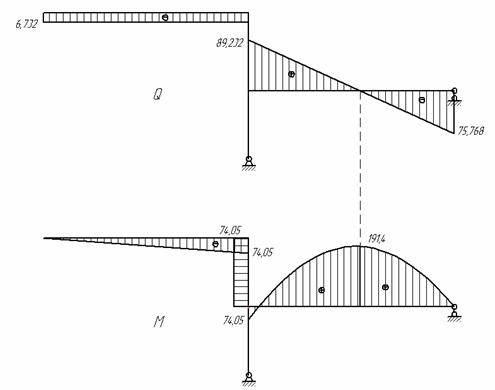
Рис.7
Расчет плоского трубопровода на температурное воздействие и
внутреннее давление
Основные определения
Известно, что в статически неопределимых стержневых конструкциях возникают напряжения в результате температурного воздействия. Температурные напряжения особенно велики в стержне, защемленном по двум концам. Для уменьшения температурных напряжений в такого рода конструкциях (например, в трубопроводах) используются температурные компенсаторы, которые увеличивают свободу деформаций за счет изгиба. Температурные компенсаторы представляют собой статически неопределимые рамы с двумя заделками по концам (рис. 1). В данном разделе рассматривается расчет плоских статически неопределимых рам (плоских трубопроводов) на температурное воздействие по методу упругого центра. Предполагается, что стержни рамы соединены между собой жестким образом под углом 90°, все стержни имеют одинаковую жесткость.

Рис.1
Рассматриваемые рамы являются три раза статически неопределимыми системами. Выберем основную систему для рамы, показанной на рис. 1, а, отбросив левую заделку (рис. 2). Лишними неизвестными являются реакции в защемлении: Х1, Х2 и Х3. В точке О поместим начало декартовой системы координат хОy. Положительное направление силы Х1 должно совпадать с направлением оси х, силы Х2 – с направлением оси y. Положительное направление пары сил Х3 должно соответствовать направлению поворота оси х к оси y. Можно показать, что решение канонической системы уравнений метода сил для выбранной основной системы дает такие формулы для определения лишних неизвестных:
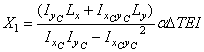 ; (1)
; (1)
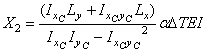 ; (2)
; (2)
![]() .
(3)
.
(3)
В этих
формулах ![]() – изменение
температуры;
– изменение
температуры; ![]() – коэффициент
линейного температурного расширения; EI
– жесткость стержней рамы; Lx, Ly – суммарные длины
стержней рамы, параллельных осям х и y. При вычислении длины стержня
учитывается направление обхода по длине стержня от начала координат. Если обход
осуществляется по направлению оси, то длина участка рамы считается
положительной, в противном случае – отрицательной. Например, для рамы,
показанной на рис. 2, Ly =
0, так как обход левой стойки рамы от начала координат происходит по направлению
оси y, а обход правой стойки – против
направления оси.
– коэффициент
линейного температурного расширения; EI
– жесткость стержней рамы; Lx, Ly – суммарные длины
стержней рамы, параллельных осям х и y. При вычислении длины стержня
учитывается направление обхода по длине стержня от начала координат. Если обход
осуществляется по направлению оси, то длина участка рамы считается
положительной, в противном случае – отрицательной. Например, для рамы,
показанной на рис. 2, Ly =
0, так как обход левой стойки рамы от начала координат происходит по направлению
оси y, а обход правой стойки – против
направления оси.

Рис.2
Чтобы
пояснить, что такое хс, yc, ![]() ,
, ![]() и
и ![]() , будем рассматривать раму как плоскую фигуру, состоящую из
прямоугольников. Одна сторона каждого прямоугольника равна длине участка рамы, а другая сторона
(толщина) всегда равна 1. Например, рама на рис. 2 считается плоской
фигурой, состоящей из пяти прямоугольников с длинами соответственно l1, l2, l3
и 2l4 и толщиной всех прямоугольников, равной 1. Тогда хс, yc – координаты центра тяжести этой плоской фигуры в
системе координат xОy. Центр тяжести
фигуры (точка С на рис. 2, б) называется упругим центром. Через
упругий центр проведем центральные оси xc,
yc, параллельные осям x, y.
В формулах (1), (2)
, будем рассматривать раму как плоскую фигуру, состоящую из
прямоугольников. Одна сторона каждого прямоугольника равна длине участка рамы, а другая сторона
(толщина) всегда равна 1. Например, рама на рис. 2 считается плоской
фигурой, состоящей из пяти прямоугольников с длинами соответственно l1, l2, l3
и 2l4 и толщиной всех прямоугольников, равной 1. Тогда хс, yc – координаты центра тяжести этой плоской фигуры в
системе координат xОy. Центр тяжести
фигуры (точка С на рис. 2, б) называется упругим центром. Через
упругий центр проведем центральные оси xc,
yc, параллельные осям x, y.
В формулах (1), (2) ![]() ,
, ![]() и
и ![]() – осевые и центробежный моменты инерции рассматриваемой плоской фигуры
относительно центральных осей xc,
yc.
– осевые и центробежный моменты инерции рассматриваемой плоской фигуры
относительно центральных осей xc,
yc.
Напомним некоторые формулы. Координаты центра тяжести плоской фигуры находим так:
![]() ;
; ![]() , (4)
, (4)
где А – площадь фигуры. В данном случае, так
как толщина всех прямоугольников равна единице, площадь равна сумме длин всех
участков рамы. Для рамы на рис. 4.46 ![]() ; Sx, Sy – статические моменты
фигуры относительно осей x, y, которые находятся как суммы статических
моментов каждого прямоугольника относительно осей x, y. Статический момент
каждого прямоугольника равен произведению площади прямоугольника на координату
центра тяжести прямоугольника в системе координат хОy.
; Sx, Sy – статические моменты
фигуры относительно осей x, y, которые находятся как суммы статических
моментов каждого прямоугольника относительно осей x, y. Статический момент
каждого прямоугольника равен произведению площади прямоугольника на координату
центра тяжести прямоугольника в системе координат хОy.
Моменты инерции плоской фигуры вычисляются как суммы моментов инерции простых фигур, составляющих данную фигуру, в рассматриваемом случае момент инерции всей фигуры равен сумме моментов инерций прямоугольников единичной толщины. Для каждого прямоугольника справедливы формулы
![]() ;
(5)
;
(5)
![]() ;
(6)
;
(6)
![]() ,
(7)
,
(7)
где ![]() – площадь прямоугольника
(
– площадь прямоугольника
(![]() ,
, ![]() ); a, b – координаты центра тяжести
прямоугольника в системе координатных осей xc,
yc;
); a, b – координаты центра тяжести
прямоугольника в системе координатных осей xc,
yc; ![]() ,
, ![]() – моменты инерции
прямоугольника относительно собственных центральных осей x0, y0,
параллельных осям xc, yc. Если ось x0 (или y0)
расположена вдоль рассматриваемого участка трубопровода, то есть параллельна
стороне прямоугольника li,
то можно считать
– моменты инерции
прямоугольника относительно собственных центральных осей x0, y0,
параллельных осям xc, yc. Если ось x0 (или y0)
расположена вдоль рассматриваемого участка трубопровода, то есть параллельна
стороне прямоугольника li,
то можно считать ![]() (или
(или ![]() ). Если же ось x0
(или y0) перпендикулярна
стороне li, то
). Если же ось x0
(или y0) перпендикулярна
стороне li, то ![]() . В формуле (7) учтено, что центробежный момент инерции
прямоугольника
. В формуле (7) учтено, что центробежный момент инерции
прямоугольника ![]() относительно собственных осей x0, y0 равен нулю, так как эти оси являются главными осями
инерции прямоугольника.
относительно собственных осей x0, y0 равен нулю, так как эти оси являются главными осями
инерции прямоугольника.
После определения величин лишних неизвестных по формулам (1) – (3) строим эпюры внутренних усилий в основной системе, как в обычной статически определимой раме. Эпюру изгибающих моментов можно проверить следующим образом. В упругом центре приложим найденные силы Х1 и Х2, нарисовав их в масштабе. Определим графически равнодействующую этих сил. Точки пересечения линии действия этой равнодействующей с осью рамы – это точки, в которых изгибающий момент должен равняться нулю (точки A, B, D на рис. 2, б).
Построив эпюры
внутренних усилий, проверим прочность конструкции, имея в виду, что поперечное
сечение стержней рамы – труба и, кроме температурного воздействия, труба
испытывает действие внутреннего давления. Максимальные
нормальные напряжения ![]() , действующие на площадках, перпендикулярных оси трубы,
находим, складывая напряжения от продольной силы и максимального изгибающего
момента в опасном сечении рамы (при определении напряжений от изгиба на
криволинейных участках трубы в местах сопряжения вертикальных и горизонтальных
стержней рамы не учитываем эффект Кармана, связанный со сплющиванием
поперечного сечения трубы и приводящий к уменьшению изгибных напряжений):
, действующие на площадках, перпендикулярных оси трубы,
находим, складывая напряжения от продольной силы и максимального изгибающего
момента в опасном сечении рамы (при определении напряжений от изгиба на
криволинейных участках трубы в местах сопряжения вертикальных и горизонтальных
стержней рамы не учитываем эффект Кармана, связанный со сплющиванием
поперечного сечения трубы и приводящий к уменьшению изгибных напряжений):
![]() .
(8)
.
(8)
Для проверки
прочности трубы из пластичного материала по формуле (8) находим максимальное по
модулю напряжение. Если труба выполнена из хрупкого материала, при проверке
прочности важен знак напряжений. Кольцевое напряжение ![]() , возникающее от внутреннего давления q, определяем по формуле
, возникающее от внутреннего давления q, определяем по формуле
![]() ,
(9)
,
(9)
где R и ![]() – соответственно
внешний радиус и толщина трубы. Напряжение
– соответственно
внешний радиус и толщина трубы. Напряжение ![]() всегда растягивающее.
На рис. 3, а показана эпюра
распределения напряжений
всегда растягивающее.
На рис. 3, а показана эпюра
распределения напряжений ![]() в опасном сечении при
положительной продольной силе. Рис. 3, б
изображает напряженное состояние опасных точек 1, 1¢. Так как касательные
напряжения на площадках элементов, показанных на рис. 3, б, отсутствуют, то эти площадки
являются главными. Проверку прочности в опасных точках осуществляем по теории
прочности, соответствующей материалу трубы.
в опасном сечении при
положительной продольной силе. Рис. 3, б
изображает напряженное состояние опасных точек 1, 1¢. Так как касательные
напряжения на площадках элементов, показанных на рис. 3, б, отсутствуют, то эти площадки
являются главными. Проверку прочности в опасных точках осуществляем по теории
прочности, соответствующей материалу трубы.

Рис.3
Пример 27.
Трубопровод, показанный на рис. 4, а, нагревается на ![]() градусов и подвержен
действию внутреннего давления q.
Труба имеет внешний радиус поперечного сечения R и толщину
градусов и подвержен
действию внутреннего давления q.
Труба имеет внешний радиус поперечного сечения R и толщину ![]() . Известен материал трубы. Требуется найти напряженное
состояние и обеспечить выполнение условия прочности трубопровода.
. Известен материал трубы. Требуется найти напряженное
состояние и обеспечить выполнение условия прочности трубопровода.
Решение.
Выберем
основную систему, отбросив левое закрепление и приложив реактивные силы (лишние
неизвестные) Х1, Х2 и Х3 (рис. 4, б). Для определения значений лишних неизвестных по формулам (1) –
(3) найдем сначала положение упругого центра и геометрические характеристики ![]() ,
,![]() и
и ![]() .
.

Рис.4
Координаты упругого центра в системе координат xОy сосчитаем по формулам (4), где
![]() м.
м.
Статический момент относительно оси х равен сумме статических моментов четырех прямоугольников единичной толщины:
![]() .
.
Статический
момент третьего участка трубопровода (третьего прямоугольника) ![]() , так как центр тяжести этого прямоугольника лежит на оси х, а статические моменты остальных
прямоугольников найдем следующим образом:
, так как центр тяжести этого прямоугольника лежит на оси х, а статические моменты остальных
прямоугольников найдем следующим образом:
![]() м2,
м2,
где ![]() – площадь первого
прямоугольника, а (
– площадь первого
прямоугольника, а (![]() ) – координата центра тяжести. Аналогично
) – координата центра тяжести. Аналогично
![]() м2,
м2,
![]() м2.
м2.
Таким образом,
![]() м.
м.
Вторая координата упругого центра
![]() м.
м.
Отложим эти координаты на рисунке и покажем точку С – упругий центр. Проведем через точку С центральные оси xc, yc (рис. 4, в). Найдем моменты инерции фигуры относительно этих осей. Момент инерции относительно оси хс равен сумме моментов инерции четырех прямоугольников:
![]() .
.
Сосчитаем момент инерции первого прямоугольника относительно оси хс по формуле (5). Для рассматриваемого прямоугольника собственная ось х0 перпендикулярна стороне l1, поэтому первый член в (5) (момент инерции первого прямоугольника собственной оси х0 ) не равен нулю. Таким образом, момент инерции относительно оси хс
![]() м3.
м3.
Для второго прямоугольника момент инерции относительно
оси хс
![]() м3.
м3.
Поскольку ось х0
параллельна стороне прямоугольника l2,
то первое слагаемое в формуле (5) отсутствует (![]() ). Аналогично находим моменты инерции остальных
прямоугольников:
). Аналогично находим моменты инерции остальных
прямоугольников:
![]() м3;
м3;
![]() м3.
м3.
И полный
момент инерции относительно оси хс
равен ![]() м3. Так же вычислим момент инерции относительно
оси yc каждого прямоугольника:
м3. Так же вычислим момент инерции относительно
оси yc каждого прямоугольника:
![]() м3;
м3;
![]() м3;
м3;
![]() м3;
м3;
![]() м3.
м3.
Полный момент
инерции относительно оси yc
равен сумме моментов инерции всех прямоугольников ![]() м3.
м3.
Найдем центробежный момент инерции. Момент инерции каждого прямоугольника определим по формуле (7). Обратим внимание на то, что, если при вычислении осевых моментов инерции знаки координат а и b можно опускать, так как они входят в формулы (5), (6) в квадрате, то при вычислении центробежного момента инерции эти знаки следует обязательно учитывать. Тогда
![]() м3;
м3;
![]() м3;
м3;
![]() м3;
м3;
![]() м3.
м3.
Полный
центробежный момент инерции ![]() м3.
м3.
Длины
трубопровода вдоль осей х и y: ![]() м,
м, ![]() м. Подставляя найденные геометрические характеристики в
формулы (1)–(3), сосчитаем значения лишних неизвестных:
м. Подставляя найденные геометрические характеристики в
формулы (1)–(3), сосчитаем значения лишних неизвестных:
![]() м–2;
м–2;
![]() м–2;
м–2;
![]() м–1.
м–1.
Нарисуем
основную систему и приложим в точке О найденные
опорные реакции. Так как все лишние неизвестные оказались положительными, то
сохраняем выбранное ранее направление всех неизвестных (рис.5, а). Построим эпюры продольных сил
и изгибающих моментов в долях от ![]() (рис. 5, б, в). На рис. 5, в
показана равнодействующая сил Х1 и Х2,
приложенных в упругом центре. Видно, что на линии действия этой
равнодействующей изгибающий момент равен нулю.
(рис. 5, б, в). На рис. 5, в
показана равнодействующая сил Х1 и Х2,
приложенных в упругом центре. Видно, что на линии действия этой
равнодействующей изгибающий момент равен нулю.
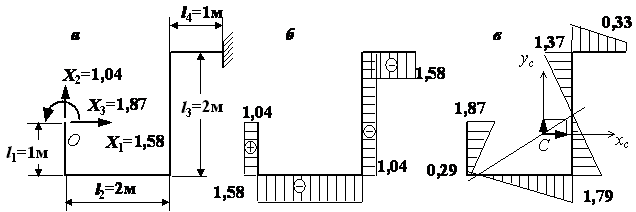
Рис.5
Теперь можно
решать вопрос о проверке прочности трубы. По эпюрам N и М находим опасное
сечение. У нас это сечение в точке О
(рис. 5, а). В этом сечении действуют одновременно
максимальный изгибающий момент и растягивающая продольная сила: ![]() ,
, ![]() . Напряжения
в опасных точках вычисляем по формулам (8) и (9). Для удобства расчетов
приведем формулу (8) к другому виду. Максимальное напряжение от изгиба
. Напряжения
в опасных точках вычисляем по формулам (8) и (9). Для удобства расчетов
приведем формулу (8) к другому виду. Максимальное напряжение от изгиба
![]() ,
,
так как момент
сопротивления ![]() . Нормальное
напряжение, вызванное продольной силой, найдем так:
. Нормальное
напряжение, вызванное продольной силой, найдем так:
![]() ,
,
где учтено, что для трубы
![]() ,
, ![]() ,
,
r – внутренний радиус трубы. Суммарные
напряжения на площадках, перпендикулярных оси х, находим согласно (8), складывая ![]() и
и ![]() .
.
Отметим особенность решаемой задачи об определении температурных напряжений в статически неопределимой раме: чем больше размер поперечного сечения (больше радиус трубы), тем больше возникающие в конструкции температурные напряжения. Это связано с тем, что с увеличением радиуса увеличивается жесткость рамы и уменьшается свобода деформаций, что и приводит к увеличению напряжений.
Вычисляя
напряжения в опасных точках, обратите внимание на единицы измерения величин,
входящих в формулы для напряжений. В формуле для определения ![]() число 1,87 имеет размерность м–1, в
формуле для
число 1,87 имеет размерность м–1, в
формуле для ![]() число 1,04 измеряется в м–2. Таким
образом, подставляя R в метрах,
получим величину напряжения в тех же единицах измерения, что и модуль упругости
Е. При проверке прочности в опасных
точках трубы используйте знания, полученные при изучении лекции
"Исследование плоского напряженного состояния. Проверка прочности для
сложного напряженного состояния". Если условие прочности выполняться не
будет, следует уменьшить радиус трубы и добиться удовлетворения условия
прочности.
число 1,04 измеряется в м–2. Таким
образом, подставляя R в метрах,
получим величину напряжения в тех же единицах измерения, что и модуль упругости
Е. При проверке прочности в опасных
точках трубы используйте знания, полученные при изучении лекции
"Исследование плоского напряженного состояния. Проверка прочности для
сложного напряженного состояния". Если условие прочности выполняться не
будет, следует уменьшить радиус трубы и добиться удовлетворения условия
прочности.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов

