Главная
Лекция 2 (продолжение). Примеры решения на осевое растяжение – сжатие
Расчеты на растяжение и сжатие
статически определимых стержневых систем
Пример 1.
Абсолютно
жесткий брус ВС (ЕВС = ![]() ) прикреплен в точке С к неподвижному шарниру (см.
рис.), а в точке В поддерживается
стальной тягой АВ. В точке В приложена вертикальная сила F = 20 кН.
) прикреплен в точке С к неподвижному шарниру (см.
рис.), а в точке В поддерживается
стальной тягой АВ. В точке В приложена вертикальная сила F = 20 кН.

Подобрать
сечение тяги АВ и показать перемещение
точки В. Расчетное сопротивление
стали растяжению ![]() коэффициент условий работы
коэффициент условий работы ![]() а модуль упругости
стали тяги АВ –
а модуль упругости
стали тяги АВ – ![]()
Решение.
Вырежем мысленно узел В (рис. б) и составим для него уравнения равновесия:
![]() откуда находим
откуда находим![]()
![]() откуда
откуда ![]()
Окончательно
имеем ![]()
![]()
Следовательно, брус ВС сжат силой N2, а элемент АВ растянут силой N1.
Подбор сечения
тяги АВ проводим по формуле ![]() откуда определяем
откуда определяем
![]()
Предположим,
что тяга АВ имеет круглое поперечное
сечение, тогда An =
1,44 см2 = ![]() , откуда находим r =
0,677 см и d = 1,35 см.
, откуда находим r =
0,677 см и d = 1,35 см.
Определим удлинения стержней АВ и СВ:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Таким образом, точка В переместится в точку В/
по дуге окружности радиусом
Таким образом, точка В переместится в точку В/
по дуге окружности радиусом ![]() , причем расстояние между точками А и В/ будет равно
, причем расстояние между точками А и В/ будет равно ![]()
Пример 2.
Определить из расчетов на прочность и жесткость
допускаемую силу F, если [![]() ] = 120 МПа, [
] = 120 МПа, [![]() ] =
] =

Р е ш е н и е.
1. Определение усилий в стержнях.
Из условия равновесия бруса АС имеем
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() .
.
2. Расчет на прочность.
Находим напряжения в
стержнях
![]() ,
,
![]() .
.
Как видим, наиболее
нагруженным является 2-й стержень, прочность которого предопределяет прочность
всей конструкции в целом. Из условия прочности ![]() находим
находим ![]() = 30 кН.
= 30 кН.
3. Расчет на жесткость.
Вычисляем деформации
стержней
![]() ,
,
![]() ,
,
а по ним перемещение точки С. Из подобия треугольников В1А1В2 и С1А1С2 имеем:
В1В2/А1В2 = С1С2/А1С2 или ![]() ,
,
откуда ![]() .
.
Записываем условие жесткости ![]() ,
,
откуда ![]() = 200×109×5×10-4×1,7×10-3/(8,5×1)= 20 кН.
= 200×109×5×10-4×1,7×10-3/(8,5×1)= 20 кН.
Допускаемая нагрузка из расчета на жесткость
получилась меньше, чем из расчета на прочность, поэтому ее и принимаем в качестве окончательной, т.е.
![]() кН.
кН.
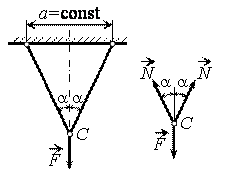
Пример 3.
К двум
одинаковым стержням приложена сила F.
Установить, при каком угле ![]() конструкция будет
иметь наименьший вес?
конструкция будет
иметь наименьший вес?
Р е ш е н и е.
Вес
конструкции является функцией угла ![]() , т.е.
, т.е. ![]() .
.
Нам необходимо установить такой угол, при котором
функция ![]() принимает минимальное значение. В теории оптимального
проектирования она называется целевой функцией.
принимает минимальное значение. В теории оптимального
проектирования она называется целевой функцией.
Для определения веса стержневой системы нужно знать площади сечений стержней. Из условия равновесия узла С находим усилия в стержнях:
![]() ,
, ![]() ,
, ![]() ,
,
а из условия прочности – площади их поперечных сечений:
![]() , откуда
, откуда ![]() .
.
Учитывая, что
длины стержней ![]() , находим вес конструкции (целевую функцию):
, находим вес конструкции (целевую функцию):
![]() .
.
Функция ![]() принимает минимальное
значение, когда
принимает минимальное
значение, когда
![]() , откуда
, откуда ![]() и
и ![]() .
.
Определение грузоподъемности
статически определимой конструкции, работающей на растяжение-сжатие. Расчет по
допускаемым напряжениям
При таком подходе несущая способность конструкции отождествляется с несущей способностью наиболее нагруженного элемента. Последовательность расчета при этом выглядит следующим образом.
Составляются уравнения статики и по числу лишних неизвестных –
дополнительные уравнения совместности деформаций. Решая полученную систему,
определяют усилия в стержнях и связанные с ними напряжения. Из сопоставления
напряжений в наиболее нагруженном элементе с допустимой величиной делается
заключение о надежности конструкции либо определяются искомые величины (размеры
сечения стержней, допускаемая нагрузка).
Пример 4.
Конструкция, состоящая из стержней, соединенных шарнирами, загружена силой F (см. рис. 1). Сечения стержней – из прокатной стали и площади сечений можно найти по таблицам сортамента прокатной стали. Цель расчета:
1. определить значение допускаемой нагрузки;
2. найти перемещение узла С.

Рис.1
Решение.
Для определения усилий используем метод сечений. Для этого нарисуем план сил (рис.2): рассечем деформируемые стержни конструкции и отброшенные части стержней заменим продольными силами N1 и N2 .

Рис.2
Из уравнений равновесия отсеченной части конструкции найдем продольные силы в стержнях:
![]() и
и ![]() .
.
Знак минус показывает, что направление усилия в стержне 2 противоположно показанному на плане сил, т.е. стержень 2 сжат.
Определим
напряжения по ![]() и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче
это будет стержень 1).
и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче
это будет стержень 1).
Из условия прочности этого стержня получим значение допускаемой нагрузки:
![]() ,
, ![]() .
.
Найдем перемещение узла С, построив план перемещений (рис.3).

Рис.3
Предварительно
найдем абсолютные деформации стержней ![]() и
и ![]() по формуле
по формуле ![]() . В
рассматриваемой задаче растянутый стержень 1 будет удлиняться, а сжатый
стержень 2 – укорачиваться. Для построения плана перемещений нарисуем схему
конструкции в масштабе и отложим отрезки
. В
рассматриваемой задаче растянутый стержень 1 будет удлиняться, а сжатый
стержень 2 – укорачиваться. Для построения плана перемещений нарисуем схему
конструкции в масштабе и отложим отрезки ![]() и
и ![]() вдоль оси каждого
стержня, выбрав масштаб для деформаций так, чтобы картинка плана перемещений
была наглядной. В процессе деформации стержни поворачиваются относительно точек
А и В по дугам. Из-за малости деформаций эти дуги заменяем
касательными, т. е. перпендикулярами к направлениям стержней (отрезки
вдоль оси каждого
стержня, выбрав масштаб для деформаций так, чтобы картинка плана перемещений
была наглядной. В процессе деформации стержни поворачиваются относительно точек
А и В по дугам. Из-за малости деформаций эти дуги заменяем
касательными, т. е. перпендикулярами к направлениям стержней (отрезки ![]() и
и ![]() на плане перемещений).
На пересечении дуг (перпендикуляров к направлениям стержней) находится новое
положение узла C после деформации –
точка
на плане перемещений).
На пересечении дуг (перпендикуляров к направлениям стержней) находится новое
положение узла C после деформации –
точка ![]() на плане перемещений.
Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных
геометрических выкладок.
на плане перемещений.
Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных
геометрических выкладок.
Примечание. Если конструкция имеет
абсолютно жесткий стержень, то принцип
построения плана перемещений тот же. Все точки абсолютно жесткого стержня могут
перемещаться только по дугам (перпендикулярам к направлению стержня), поворачиваясь
вокруг неподвижного шарнира. Например, если стержень АС на плане перемещений считать абсолютно жестким, то точка С переместится в положение ![]() и горизонтальное
перемещение узла С будет равно нулю.
и горизонтальное
перемещение узла С будет равно нулю.
Пример 5.
Для схемы, изображенной на рис.1 необходимо:
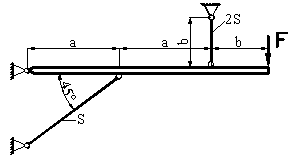
Рис.1
1) Определить площадь поперечного сечения стержней при действии силы F и подобрать угловую равнополочную или неравнополочную сталь, при условии, что поперечное сечение одного из стержней в два раза больше, чем другого.
2) Определить напряжения в стержнях:
- от действия силы F;
- от неточности монтажа, если считать, что один из стержней выполнен
короче на величину ![]() ;
;
- от изменения температуры.
3) Определить суммарные напряжения от действия внешних сил, от неточности монтажа и от изменения температуры.
4) Подсчитать недонапряжения или перенапряжения в стержнях.
Дано: F=100 кН, а =
1,2м, b = 0,8м, ![]() = 0,2мм,
= 0,2мм, ![]() = 20°С, Е = 2×105МПа,
= 20°С, Е = 2×105МПа,
![]() = 125×10-71/гр, [
= 125×10-71/гр, [![]() ] = 100 МПа.
] = 100 МПа.
Решение.
Определим необходимую по условию прочности площадь поперечного сечения стержней.
1) Находим степень статической неопределимости.
![]()
2.1) Статическая сторона задачи
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
2.2) Геометрическая сторона задачи (рис.2)
![]() ~
~![]() Þ
Þ
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
2.3) Физическая сторона задачи
![]() ;
; ![]()
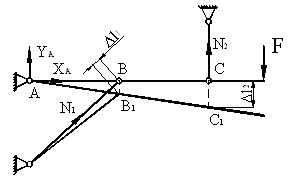
Рис.2
2.4) Синтез
Подставим выражения, полученные в физической стороне задачи, в выражения из геометрической стороны задачи и приведем подобные.
![]()
![]()
![]()
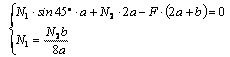
Решим совместно систему уравнений, составленную из полученного выражения для N1 и уравнения моментов из статической стороны задачи.
![]()
![]()
![]()
![]()
2.5) Определяем площадь поперечного сечения стержней
Определим, какой из стержней нагружен сильнее.
![]() ;
; ![]()
Второй стержень является более нагруженным, так как ![]() , поэтому запишем для него условие прочности и
определим площадь поперечного сечения.
, поэтому запишем для него условие прочности и
определим площадь поперечного сечения.
![]()
Подбираем по справочнику угловую равнополочную сталь № 70´5 ГОСТ8509-86 (SТ = 6,86 см2).
2.6) Определяем напряжения в стержнях от внешних сил
![]()
![]()
Первый стержень работает на сжатие, а второй – на растяжение.
3) Определим напряжения в стержнях от неточности монтажа
Будем считать, что короткий стержень выполнен короче на величину ![]() (см.рис.3).
(см.рис.3).
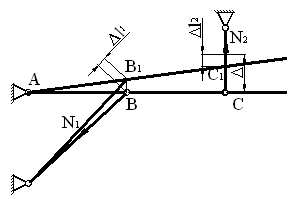
Рис.3
3.1) Статическая сторона задачи
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
3.2) Геометрическая сторона задачи
![]() ~
~![]() Þ
Þ
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
3.3) Физическая сторона задачи
![]() ;
;
![]()
3.4) Синтез
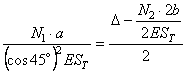
![]()
Подставим в полученное выражение данные из условия задачи и получим:
![]()
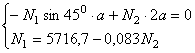
![]()
![]()
![]()
![]()
3.5) Определим напряжения в стержнях
![]()
![]()
Оба стержня работают на растяжение.
4) Определим напряжения в стержнях от изменения температуры (см. рис. 4).
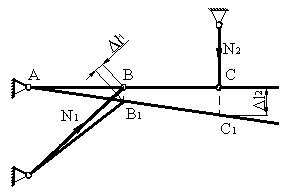
Рис.4
Будем считать, что температура системы повышается. Тогда оба стержня будут удлиняться от повышения температуры. При удлинении стержней, они будут воздействовать друг на друга через недеформируемый стержень АС. Вследствие этого, в обоих стержнях будут возникать дополнительные силы сжатия.
4.1) Статическая сторона задачи
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
4.2) Геометрическая сторона задачи
![]() ~
~![]() Þ
Þ
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
4.3) Физическая сторона задачи
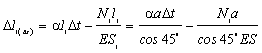 ;
;
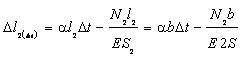 .
.
4.4) Синтез
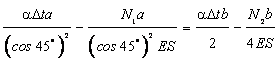

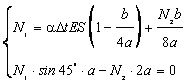

Решив уравнение, получим ![]() .
.
![]()
4.5) Определим напряжения в стержнях
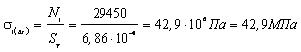
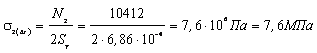
Оба стержня работают на сжатие.
5) Определим суммарные напряжения в стержнях
![]()
![]()
6) Найдем недонапряжения или перенапряжения в стержнях
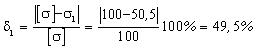 - недонапряжение
- недонапряжение
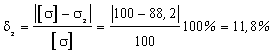 - недонапряжение.
- недонапряжение.
Пример 6.
Дано: Сила F= 100 кН; расчетное сопротивление стали R =160 МПа; модуль упругости E=2∙105 МПа (рис. а)
Требуется:
1. Определить усилия в стержнях.
2. Подобрать размеры поперечных сечений стержней. Стержень 1 стальной, круглого поперечного сечения, стержень 2 стальной квадратного сечения.
3. Вычислить удлинения (укорочения) стержней и построить план перемещений.
4. Определить перемещение узла.
а)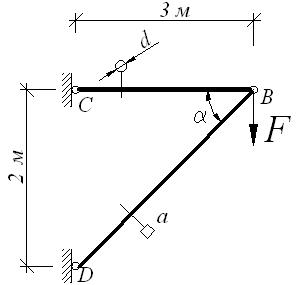 б)
б)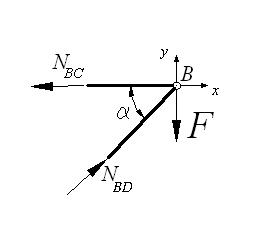
в)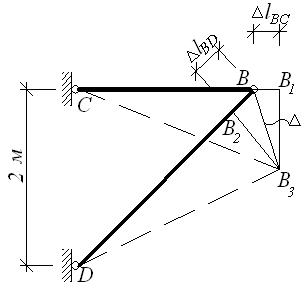 г)
г)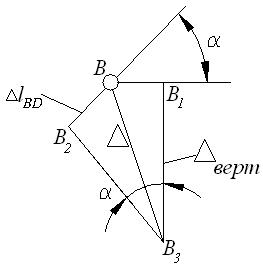
Решение.
Мысленно вырезаем узел В, действие отброшенной части кронштейна заменяем искомыми внутренними усилиями. Для полученной плоской системы сходящихся сил составим уравнения равновесия (рис. б)
![]()
Решив
уравнения, найдем внутренние усилия NBD и NBC
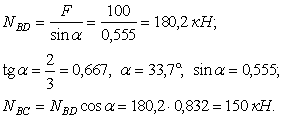
Полученные положительные значения внутренних усилий показывают, что предварительно выбранные направления усилий оказались верными, стержень BC растягивается, а стержень BD сжимается.
Диаметр стержня BC находим из условия прочности:
![]()
где![]() ,
,
откуда  .
.
Размеры поперечного сечения стержня BD определим на условия
прочности:
![]()
где ABD = a2,
откуда 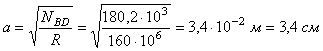 .
.
Перемещение узла В найдем с помощью графоаналитического метода, для чего вычислим, используя закон Гука, абсолютные деформации стержней ВС и BD, предполагая их свободными в точке В:
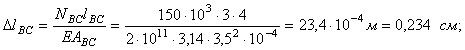
![]()
где ![]()
Положение узла В после деформации стержней
определится в результате построения
деформационного треугольника по сторонам ![]() и
и ![]() .
.
Стержень ВС удлинился на величину ![]() , концевое сечение
переместилось в точку В1
. Радиусом, равным СВ1
проведем из точки С
дугу окружности. Так как перемещения малы, то дугу можно заменить касательной,
проведенной через В1
перпендикулярно оси стерня ВС
(рисунок 1, в).
, концевое сечение
переместилось в точку В1
. Радиусом, равным СВ1
проведем из точки С
дугу окружности. Так как перемещения малы, то дугу можно заменить касательной,
проведенной через В1
перпендикулярно оси стерня ВС
(рисунок 1, в).
Стержень BD укоротился на ![]() , и концевое сечение переместилось в точку В2.
Заменяя дугу, описанную из точки D радиусом DB2 касательной,
проведенной через В2
перпендикулярно оси стержня BD, получим на
пересечении перпендикуляров точку В3
- новое положение узла В. Соединив
точку В с В3 найдем перемещение
, и концевое сечение переместилось в точку В2.
Заменяя дугу, описанную из точки D радиусом DB2 касательной,
проведенной через В2
перпендикулярно оси стержня BD, получим на
пересечении перпендикуляров точку В3
- новое положение узла В. Соединив
точку В с В3 найдем перемещение ![]() узла В. На рисунке 1, в план перемещений изображен в увеличенном масштабе. План
перемещений рекомендуется строить отдельно, как показано на рисунке 1, г. Из него следует, что горизонтальная
составляющая перемещения
узла В. На рисунке 1, в план перемещений изображен в увеличенном масштабе. План
перемещений рекомендуется строить отдельно, как показано на рисунке 1, г. Из него следует, что горизонтальная
составляющая перемещения ![]() узла
В равна:
узла
В равна:
![]() см.
см.
Вертикальную
составляющую перемещения ![]() узла
В легко найти,
воспользовавшись теоремой аналитической геометрии – проекция замыкающей на
любую ось равна алгебраической сумме проекций составляющих на ту же ось. Принимая за ось проекций направление
узла
В легко найти,
воспользовавшись теоремой аналитической геометрии – проекция замыкающей на
любую ось равна алгебраической сумме проекций составляющих на ту же ось. Принимая за ось проекций направление ![]() получим:
получим:
![]() ;
;
откуда ![]() .
.
Знак ![]() учтен при построении
плана перемещений. Полное перемещение узла В будет равно:
учтен при построении
плана перемещений. Полное перемещение узла В будет равно:
![]() .
.
Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов