Главная
Лекция 2 (продолжение). Примеры решения на осевое растяжение – сжатие
Расчет статически неопределимых
стержней при растяжении-сжатии
Статически неопределимыми системами называются системы, для которых реакции связей и внутренние усилия не могут быть определены только из уравнений равновесия. Поэтому при их расчете необходимо составлять дополнительные уравнения перемещений, учитывающие характер деформации системы. Число дополнительных уравнений, необходимых для расчета системы, характеризует степень ее статической неопределимости. Способы составления уравнений перемещений будут рассмотрены на примерах решения различных задач.
Пример 1.
Статически
неопределимыми называются такие конструкции, в элементах которых при помощи
только одних уравнений статики определить усилия невозможно. Например, на рис.1
показан ступенчатый стержень, жестко закрепленный в точках ![]() и
и ![]() . На стержень действуют силы
. На стержень действуют силы ![]() и
и ![]() . Модуль продольной упругости материала стержня
. Модуль продольной упругости материала стержня ![]() . Площади поперечных сечений участков:
. Площади поперечных сечений участков: ![]() ;
; ![]() ;
; ![]() . Длина участка
. Длина участка ![]() . Необходимо раскрыть статическую неопределимость, определить
продольные усилия, возникающие в различных частях стержня, нормальные
напряжения и перемещения различных точек стержня при заданной нагрузке.
. Необходимо раскрыть статическую неопределимость, определить
продольные усилия, возникающие в различных частях стержня, нормальные
напряжения и перемещения различных точек стержня при заданной нагрузке.
Решение.
Заменим действие опор на стержень реакциями (![]() и
и ![]() ) и составим уравнение проекций сил на ось стержня (ось
) и составим уравнение проекций сил на ось стержня (ось ![]() ):
):
![]() ;
; ![]() , (1)
, (1)
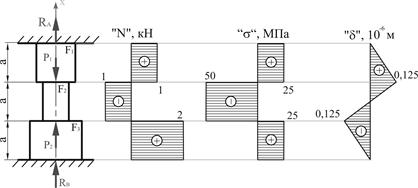
Рис. 1
Остальные
уравнения статики дадут нам такое же выражение (1). В одно уравнение входят два
неизвестных усилия (![]() и
и ![]() ), следовательно, задача один раз статически неопределима.
), следовательно, задача один раз статически неопределима.
Для расчета таких систем необходимо использовать уравнения, содержащие деформации элементов конструкций. Так как концы стержня жестко закреплены, то общая длина не изменяется:
![]() .
.
Общая деформация стержня будет складываться из деформаций его элементов:
![]() , (2)
, (2)
где ![]() – продольное
усилие на
– продольное
усилие на ![]() -том участке;
-том участке; ![]() – длина
– длина ![]() - того участка;
- того участка; ![]() – модуль продольной
упругости материала;
– модуль продольной
упругости материала; ![]() – площадь поперечного
сечения
– площадь поперечного
сечения ![]() - того участка.
- того участка.
Выразим
продольные усилия в поперечных сечениях стержня через одну из неизвестных
реакций ![]() .
.
Разделим стержень на участки по местам приложения сосредоточенных нагрузок и местам изменения поперечного сечения стержня. Для приведенной схемы получаем три участка (рис. 1).
Мысленно
рассечем первый участок произвольно взятым поперечным сечением и отбросим
нижнюю часть балки, заменяя ее действие на верхнюю
часть продольной силой ![]() , которую первоначально направляем в сторону
растяжения рассматриваемого элемента первого участка (рис. 2).
, которую первоначально направляем в сторону
растяжения рассматриваемого элемента первого участка (рис. 2).
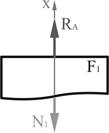
Рис. 2
Из условия равновесия:
![]()
![]() ;
; ![]() (3)
(3)
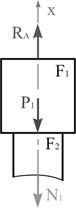
Рис. 3
Мысленно
рассечем второй участок произвольно взятым поперечным сечением и отбросим нижнюю
часть балки, заменяя ее действие на верхнюю часть
продольной силой ![]() которую
первоначально направляем в сторону растяжения рассматриваемого элемента первого
участка (рис. 3).
которую
первоначально направляем в сторону растяжения рассматриваемого элемента первого
участка (рис. 3).
Из условия
равновесия:![]()
![]() ;
;
![]() (4)
(4)
Для третьего
участка (рис. 3): ![]()
![]() ;
;
![]() (5)
(5)
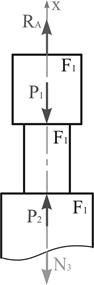
Рис. 4
Деформация участков согласно формуле (2):
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Общая деформация должна равняться нулю:
![]()
Умножив обе
части уравнения на ![]() получим:
получим:
![]() ,
,
или:
![]()
![]() .
.
Из выражения (1):
![]() (9)
(9)
Знак «-» указывает на
обратное направление реакции![]() .
.
Определяем значения осевых усилий для каждого участка по найденным ранее выражениям (3) – (5):
![]() ;
;
![]() ;
;
![]() .
.
По полученным
значениям строим эпюру осевых усилий. Для этого проводим нулевую (базовую)
линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий
(рис. 1). В одну сторону откладываем положительные значения, в другую -
отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а внутри
эпюры ставится знак откладываемой величины. Рядом указываются значения
откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («![]() ») и через запятую - единицы измерения (кН).
») и через запятую - единицы измерения (кН).
Нормальные напряжения в поперечных сечениях:
![]() (10)
(10)
![]() ;
;
![]() ;
;
![]() .
.
По полученным
значениям нормальных напряжений строим эпюру нормальных напряжений («![]() ») (рис. 1).
») (рис. 1).
Определим деформацию каждого участка:
![]() ;
;
![]() ;
;
![]() .
.
Эпюру
перемещений строим по перемещениям точек![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Сечение в
точке ![]() возьмем как базовое,
перемещение которого
возьмем как базовое,
перемещение которого ![]() . Тогда перемещение точки
. Тогда перемещение точки ![]() будет равно удлинению
первого участка:
будет равно удлинению
первого участка:
![]()
Перемещение
точки ![]() будет складываться из перемещения точки
будет складываться из перемещения точки ![]() и удлинения второго
участка:
и удлинения второго
участка:
![]()
Перемещение
точки ![]() будет складываться из перемещения точки
будет складываться из перемещения точки ![]() и удлинения второго
участка:
и удлинения второго
участка:
![]()
Перемещение ![]() является своего рода
проверкой правильности решения данной задачи, так как точка
является своего рода
проверкой правильности решения данной задачи, так как точка ![]() принадлежит неподвижной опоре.
принадлежит неподвижной опоре.
По полученным
значениям ![]() строим эпюру перемещений («
строим эпюру перемещений («![]() ») (рис. 1).
») (рис. 1).
Так как внутри
участков перемещения поперечных сечений имеют пропорциональную зависимость от
координаты сечения ![]() , значения, отложенные в точках
, значения, отложенные в точках ![]() ,
, ![]() ,
, ![]() ,
, ![]() , соединяются между собой прямыми линиями.
, соединяются между собой прямыми линиями.
Пример 2.
Задан стальной
стержень, заделанный обоими концами и нагруженный силой F = 1000 Н (рис. а).
Удельный вес материала стержня ![]() = 78,5 кН/м3, модуль упругости –
= 78,5 кН/м3, модуль упругости – ![]() .
.
Требуется
построить эпюры нормальных сил и напряжений, а также определить перемещение
сечения I – I.
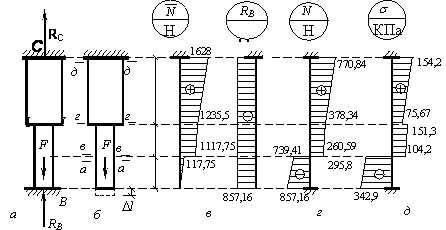
Решение.
Выбираем основную систему, которая должна представлять собой статически определимую неизменяемую систему. Основная система получается из заданной системы путем отбрасывания лишних связей и замены их действия неизвестными реакциями. Принятая основная система показана на рис. б.
Строим эпюру
нормальных сил ![]() для основной системы,
для чего определяем нормальные силы в соответствующих сечениях (рис. б):
для основной системы,
для чего определяем нормальные силы в соответствующих сечениях (рис. б):
![]()
![]()
![]()
![]()
Определяем перемещение нижнего конца стального стержня основной системы:
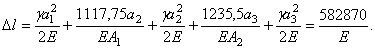
Таким образом,
если в статически неопределимом брусе (рис. а)
убрать одну нижнюю опору, то нижнее опорное сечение переместится вниз на
величину ![]() , но этого в реальном брусе не может быть, следовательно, на
опоре В
должна действовать опорная реакция RB,
от которой будет возникать линейная деформация
, но этого в реальном брусе не может быть, следовательно, на
опоре В
должна действовать опорная реакция RB,
от которой будет возникать линейная деформация ![]() , равная по величине
, равная по величине ![]() , но противоположная по знаку:
, но противоположная по знаку:
![]()
Уравнение перемещений будет иметь вид:
![]() или
или ![]() откуда находим RB = 857,16 Н.
откуда находим RB = 857,16 Н.
Опорная реакция RB вызывает в брусе сжатие, следовательно, эпюра нормальных сил от действия только опорной реакции RB будет иметь вид прямоугольника (рис. в).
Для получения
эпюры нормальных сил для статически неопределимого бруса (рис. а) следует сложить две эпюры: эпюру
нормальных сил в основной системе (рис. б)
и эпюру нормальных сил от действия опорной реакции RB (рис. в).
Сложение эпюр проводим, складывая значения нормальных сил двух эпюр в соответствующих
точках (рис. г). После чего строится
эпюра нормальных напряжений по формуле ![]()
Эпюра
нормальных напряжений ![]() показывает, что самое большое сжимающее
нормальное напряжение будет в нижнем опорном сечении (
показывает, что самое большое сжимающее
нормальное напряжение будет в нижнем опорном сечении (![]() КПа), а самое
большое растягивающее напряжение – в верхнем опорном сечении (
КПа), а самое
большое растягивающее напряжение – в верхнем опорном сечении (![]() = 154,2 КПа).
По эпюре нормальных сил находим опорную
реакцию в верхней заделке – RС = 770,84 Н.
= 154,2 КПа).
По эпюре нормальных сил находим опорную
реакцию в верхней заделке – RС = 770,84 Н.
Критерием
правильности вычислений является равенство нулю площади эпюры нормальных
напряжений, т.е. ![]() или
или ![]() , где
, где ![]() – площадь части эпюры
нормальных напряжений со знаком «плюс» (рис. д):
– площадь части эпюры
нормальных напряжений со знаком «плюс» (рис. д):
![]()
![]() – площадь части эпюры нормальных напряжений со знаком
«минус»:
– площадь части эпюры нормальных напряжений со знаком
«минус»:
![]()
В нашем случае ![]() =
=![]() = 191,6, следовательно, расчет выполнен правильно.
= 191,6, следовательно, расчет выполнен правильно.
Определим перемещение сечения I – I (рис. а), для чего применим метод сечений. Проведем сечение I – I на эпюре нормальных сил (рис. г) и отбросим нижнюю часть эпюры, тогда по оставшейся части эпюры определяем
![]()
Перемещение ![]() можно вычислить, если
отбросить верхнюю часть эпюры нормальных сил:
можно вычислить, если
отбросить верхнюю часть эпюры нормальных сил:
![]()
Получили одно и то же значение перемещений, но с разными знаками, что естественно, так как сечение I – I переместилось вниз, следовательно, верхняя часть бруса увеличила линейные размеры вдоль оси, а нижняя, наоборот уменьшила.
Пример 3.
Определить
нормальное напряжение в бетоне и арматуре железобетонной колонны, квадратное
поперечное сечение которой показано на рисунке, причем h = 30 см, модуль продольной упругости стали ![]() , а бетона тяжелого класса В 30 –
, а бетона тяжелого класса В 30 – ![]()
Решение.
В поперечном сечении колонны установлены четыре стержня диаметром 20 мм, следовательно, по справочнику принимаем, что общая их расчетная площадь поперечного сечения Аа = 12,56 см2. Площадь поперечного сечения, занимаемого бетоном, определяется как
![]()
Пусть в поперечном сечении колонны действует сжимающая сила N, тогда уравнение равновесия примет вид:
![]() .
.
Для определения усилий в арматуре Na и в бетоне Nb одного записанного выше уравнения равновесия недостаточно, так как задача один раз статически неопределима. Составим дополнительное уравнение возможных перемещений (уравнение совместности деформаций). Очевидно, что между арматурой и бетоном существует сцепление, так что абсолютное и относительное удлинения арматуры и бетона равны
![]() или
или ![]() .
.
Учитывая, что ![]() , получаем равенство относительных удлинений:
, получаем равенство относительных удлинений:
![]() или
или ![]() , или, что то же самое
, или, что то же самое ![]() откуда находим
откуда находим
![]()
Подставляя
полученное соотношение в уравнение равновесия при учете, что ![]() ,
, ![]() , и полагая, что внешняя сосредоточенная сжимающая сила N = 600 , имеем
, и полагая, что внешняя сосредоточенная сжимающая сила N = 600 , имеем
![]()
![]() откуда находим
откуда находим
![]()
Напряжения имеют знак «минус», так как колонна работает на сжатие.
Пример 4.
Задан стальной
стержень, защемленный одним концом и загруженный силой F = 1000 Н (рис. а).
Удельный вес стали стержня
![]() модуль продольной упругости
стали
модуль продольной упругости
стали ![]() .
.
Требуется
построить эпюры нормальных сил и нормальных напряжений, учитывая, что до
приложения нагрузок имелся зазор между нижним торцом бруса и нижней опорой
равный ![]()

Решение.
Если нижнюю
опору не принимать во внимание и вычислить перемещение нижнего торца стержня ![]() при учете
сосредоточенной силы F и собственного
веса стержня, то будем иметь
при учете
сосредоточенной силы F и собственного
веса стержня, то будем иметь ![]() . Полученное значение
. Полученное значение ![]() показывает, что нижний
торец бруса в этом случае должен был бы опуститься ниже уровня нижней опоры на
величину (рис. а)
показывает, что нижний
торец бруса в этом случае должен был бы опуститься ниже уровня нижней опоры на
величину (рис. а)
![]()
Но этого быть
не может, так как имеется абсолютно жесткая нижняя опора. Следовательно, будет
возникать опорная реакция RB,
которая будет препятствовать возникновению перемещения нижнего торца стержня,
равного ![]() :
:
![]()
Приравняем два
значения ![]() : 82870/Е = RB680/Е, откуда найдем значение опорной
реакции RB = 121,87 Н.
: 82870/Е = RB680/Е, откуда найдем значение опорной
реакции RB = 121,87 Н.
Эпюра нормальных
сил от действия только опорной реакции RB
будет иметь вид, показанный на рис. б.
Для построения окончательной эпюры нормальных сил для статически неопределимого
бруса, показанного на рис. а, следует
сложить две эпюры: эпюру нормальных сил в основной системе (рис. б) и эпюру нормальных сил от действия
опорной реакции RB (рис. б). Проведя сложение двух эпюр, получим
окончательную эпюру N, показанную на рис. в, а затем можно переходить к построению эпюры нормальных
напряжений ![]() (рис. г).
(рис. г).
Стержень
переменного сечения с заданным соотношением площадей поперечного сечения ![]() , выполненный из разного материала, загружен силой F (см. рис. 1). Между правым концом стержня и стенкой
существует зазор
, выполненный из разного материала, загружен силой F (см. рис. 1). Между правым концом стержня и стенкой
существует зазор ![]() .
.
Требуется:
1) определить продольные силы, напряжения на каждом участке и проверить прочность стержня от действия заданной нагрузки F.
2) найти дополнительные напряжения,
возникающие в стержне при его нагревании на температуру ![]() и проверить прочность
стержня от температурного воздействия.
и проверить прочность
стержня от температурного воздействия.
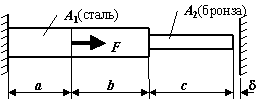
Рис.1
Решение.
Прежде всего надо убедиться, что заданная система является статически неопределимой. Найдем абсолютную деформацию стержня, показанного на рисунке, предполагая сначала, что правая стенка отсутствует. Тогда, используя метод сечений, определим продольные силы на трех участках стержня:
- на первом
участке длиной ![]() ;
;
- на втором и
третьем участках ![]() .
.
Полное
удлинение стержня, равное в общем случае ![]() , в данной задаче равно удлинению первого участка и,
следовательно, по
, в данной задаче равно удлинению первого участка и,
следовательно, по ![]()
![]() .
.
Если под действием нагрузки абсолютная деформация ![]() стержня будет больше заданного зазора
стержня будет больше заданного зазора ![]() , то стержень упрется правым концом в стенку и возникнут
опорные реакции как в левом защемлении (
, то стержень упрется правым концом в стенку и возникнут
опорные реакции как в левом защемлении (![]() ), так и в правом опорном закреплении (
), так и в правом опорном закреплении (![]() ) (рис. 2, а).
Для заданной системы можно составить только одно независимое уравнение статики
) (рис. 2, а).
Для заданной системы можно составить только одно независимое уравнение статики ![]() . Таким образом, две неизвестные опорные реакции нельзя найти
из одного уравнения, и система в процессе деформации становится один раз статически неопределимой.
. Таким образом, две неизвестные опорные реакции нельзя найти
из одного уравнения, и система в процессе деформации становится один раз статически неопределимой.

Рис.2
Для раскрытия статической неопределимости используем расчет по упругой стадии деформаций и запишем три группы уравнений:
1) уравнения равновесия. Из них получим:
- для всего
стержня ![]() ;
;
- для
отсеченных частей стержня ![]()
![]()
![]() Заметим, что
при составлении уравнений равновесия отсеченных частей стержня сделано
предположение, что первая и вторая части стержня растянуты, а третья часть –
сжата;
Заметим, что
при составлении уравнений равновесия отсеченных частей стержня сделано
предположение, что первая и вторая части стержня растянуты, а третья часть –
сжата;
2) уравнение
совместности деформаций, смысл которого в данной задаче очень простой: полная
деформация стержня равна заданному зазору. При составлении уравнения
совместности деформаций важно, чтобы знаки абсолютных деформаций
соответствовали сделанным предположениям о направлении усилий. В нашем примере ![]() ;
;
3) физические уравнения
![]()
![]()
![]() .
.
Решив
полученную систему уравнений, найдем продольные силы, а затем напряжения в
разных частях стержня и построим эпюры их распределения по длине стержня
(рис. 2, б). Если знак
усилия после решения системы уравнений получился отрицательным, это означает,
что сделанное предположение о направлении продольной силы не подтвердилось. В
рассмотренной задаче отрицательным должно получиться усилие ![]() , т. е. второй участок длиной b не растянут, а сжат. Знаки N
и s
на эпюрах ставим в соответствии с правилом знаков для продольной силы.
, т. е. второй участок длиной b не растянут, а сжат. Знаки N
и s
на эпюрах ставим в соответствии с правилом знаков для продольной силы.
После
определения напряжений производим проверку прочности по формулам ![]() или
или ![]() так же, как в
статически определимой системе. Если условие прочности на каком-нибудь участке
стержня не будет выполняться, измените значение F так, чтобы условие прочности соблюдалось.
так же, как в
статически определимой системе. Если условие прочности на каком-нибудь участке
стержня не будет выполняться, измените значение F так, чтобы условие прочности соблюдалось.
II. Определение температурных напряжений
Найдем
удлинение стержня от температурного воздействия ![]() и убедимся в том, что
это удлинение больше заданного зазора
и убедимся в том, что
это удлинение больше заданного зазора ![]() .
.
![]() .
.
Если ![]() , то система является один раз статически
неопределимой и раскрытие статической неопределимости производим по той
же схеме, что и в предыдущей части задачи:
, то система является один раз статически
неопределимой и раскрытие статической неопределимости производим по той
же схеме, что и в предыдущей части задачи:
Из уравнений
равновесия следует, что ![]() и
и ![]() . Здесь в соответствии с рис. 3, а предполагаем, что стержень всюду сжат.
(Силу F при определении температурных
напряжений считаем равной нулю.)
. Здесь в соответствии с рис. 3, а предполагаем, что стержень всюду сжат.
(Силу F при определении температурных
напряжений считаем равной нулю.)
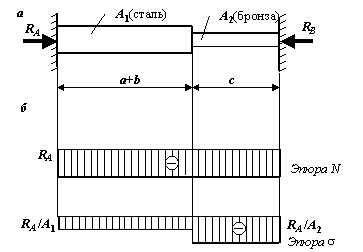
Рис.3
Уравнение
совместности деформации показывает, что абсолютная деформация стержня, равная
разности удлинения стержня от температурного воздействия![]() и укорочения
от действия сжимающих продольных сил
и укорочения
от действия сжимающих продольных сил ![]() не может быть
больше заданного зазора
не может быть
больше заданного зазора ![]() :
:
![]() ,
,
где ![]() .
.
Укорочение стержня от действия продольных сил найдем, используя физические уравнения (закон Гука):
![]() и
и 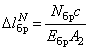 .
.
После решения полученной системы уравнений найдем усилия в обеих частях стержня. Полученный положительный знак должен подтвердить предположение о том, что стержень сжат. Строим эпюры продольной силы и напряжений (рис. 3, б) от температурного воздействия.
Проверяем
прочность стержня и в случае невыполнения условия прочности на каком-нибудь
участке находим новое значение ![]() , при
котором условие прочности будет соблюдаться на всех участках.
, при
котором условие прочности будет соблюдаться на всех участках.
Пример 6.
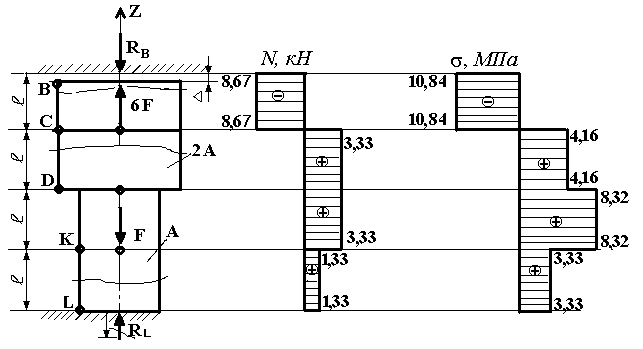
На рис.1,а изображен стальной ступенчатый брус (E = 2×105
МПа), жестко закрепленный с одной стороны. С другой стороны между стержнем и заделкой
имеется зазор ![]() = 0,01 мм. Данный
стержень нагружен осевыми силами,
выраженными через кратную нагрузку F = 2 кН, длина
участков l = 0,4 м, Е
= 2×105
МПа, а площади
поперечных сечений, выражены через А
= 4×10-4
м2.
= 0,01 мм. Данный
стержень нагружен осевыми силами,
выраженными через кратную нагрузку F = 2 кН, длина
участков l = 0,4 м, Е
= 2×105
МПа, а площади
поперечных сечений, выражены через А
= 4×10-4
м2.
Требуется:
1. Установить,
закроется ли зазор для заданной расчетной схемы.
2. Раскрыть
статическую неопределимость.
3. Построить
эпюру продольных сил и нормальных напряжений.
4. Проверить
прочность бруса, если допускаемое напряжение ![]() = 160 МПа.
= 160 МПа.
а) б) в)
Рис.1
Решение.
1. Устанавливаем
закроется ли зазор между стержнем и заделкой
от приложенных внешних нагрузок.
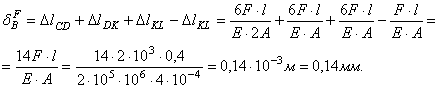
Получили, что
полная деформация бруса ![]() от действия внешних
сил больше, чем зазор
от действия внешних
сил больше, чем зазор ![]() = 0,01 мм, т.е. зазор
= 0,01 мм, т.е. зазор ![]() перекрывается и
возникает опорная реакция RB.
перекрывается и
возникает опорная реакция RB.
2. Определение степени статической
неопределимости. В результате перекрытия зазора возникает вторая опорная
реакция RB. Для заданной линейной системы
сил составим уравнение статического равновесия:
![]() ; - RB + 6F – F + RL = 0.
; - RB + 6F – F + RL = 0.
В результате
имеем два неизвестных RB и RL и одно уравнение статического равновесия. Следовательно задача один раз статически неопределима и
требуется составить еще одно уравнение – условие
совместности перемещений.
3. Раскрытие статической неопределимости.
Для
определения опорных реакций составим условие совместности перемещений для
сечения В: от действия внешних нагрузок ![]() и от силы реакции RB;
и от силы реакции RB; ![]() или
или ![]() ;
;
Согласно результатов расчета п.1 выше: ![]() .
.
Перемещение
сечения В только от реакции ![]() :
:
![]() ;
;
Тогда исходное
уравнение примет вид: ![]() ;
;
Умножаем обе
части уравнения на ЕА и делим на l:
![]() .
.
Отсюда находим
RВ :
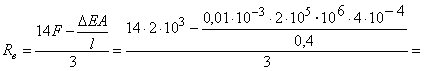
![]() .
.
Из уравнения
равновесия (см. п.2) находим вторую
реакцию RL:
![]() ;
; ![]() кН.
кН.
Полученный
знак минус перед реакцией RL
показывает, что действительное ее направление, в противоположную сторону от выбранного.
4. Построение эпюры продольных сил и нормальных
напряжений.
Далее,
используя метод сечения (рис. 2), определяем величины продольных сил на
участках стержня и строим эпюру N (рис. 2, б)
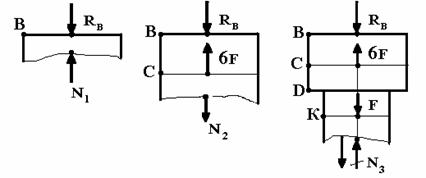
а)
б)
в)
Рис.2
Участок
ВС: ![]() ; N1 - RВ =
0; N1 = RВ = 8,67 кН.
; N1 - RВ =
0; N1 = RВ = 8,67 кН.
Участок
СК: ![]() ; N2 + 6F - RВ = 0; N2 = 6F
- RВ = 6 ×2 –8,67 = 3,33 кН.
; N2 + 6F - RВ = 0; N2 = 6F
- RВ = 6 ×2 –8,67 = 3,33 кН.
Участок KL: ![]() ; - RВ
+ 6F - F + N3
= 0; N3 = RВ
–5F = 8,67 – 5 × 10 = - 1,33 кН.
; - RВ
+ 6F - F + N3
= 0; N3 = RВ
–5F = 8,67 – 5 × 10 = - 1,33 кН.
Так как
продольная сила N3
= - 1,33 кН, то меняем на схеме рисунка 2,в направление вектора на противоположный.
Определяем
величину нормальных напряжений ![]() по участкам бруса,
строим эпюру
по участкам бруса,
строим эпюру ![]() (рис.2,в)
и сравниваем эти величины с допускаемым нормальным напряжением
(рис.2,в)
и сравниваем эти величины с допускаемым нормальным напряжением ![]() = 160 МПа.
= 160 МПа.
Участок ВС:
![]()
Сравнение ![]() выполняем по модулю.
Условие прочности выполняется.
выполняем по модулю.
Условие прочности выполняется.
Участок CD:
![]()
Условие прочности
выполняется.
Участок DK:
![]()
Условие
прочности выполняется.
Участок КL:
![]()
Условие
прочности выполняется.
Пример 7.
Определить
усилия и нормальные напряжения в стержне с зазором ![]() , изображенном на рисунке, при действии силы P и нагревании на
, изображенном на рисунке, при действии силы P и нагревании на ![]() .
.
Принять зазор ![]() =0,1 мм, а=0,5 м, F=100 см2,
P=1500 кН,
=0,1 мм, а=0,5 м, F=100 см2,
P=1500 кН, ![]() =300 С.
=300 С.
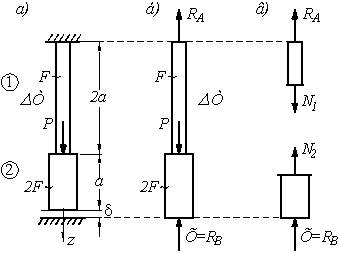
Решение.
В результате
сборки конструкции (ликвидации зазора ![]() ), действии силы P и температуры
), действии силы P и температуры ![]() в опорах возникнут
реакции
в опорах возникнут
реакции ![]() . Уравнение равновесия имеет вид
. Уравнение равновесия имеет вид
![]() .
.
Задача один
раз статически неопределима. Решаем задачу методом сил. Для эквивалентной системы составляем дополнительное уравнение
совместности деформаций. Перемещение сечения ![]() ограничено, поэтому
ограничено, поэтому
![]() .
.
Используя принцип независимости действия сил и закон Гука для эквивалентной системы получаем
![]() ,
,
или
![]() ,
,
откуда
![]() .
.
Тогда:
![]() .
.
Методом
сечения находим усилия на каждом из участков стержня:
![]()
Напряжения
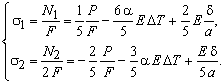
Таким образом,
каждое из слагаемых в выражениях для напряжений содержит три вида слагаемых.
Первые возникают за счет действия силы ![]() , вторые – за счет изменения температуры (температурные
напряжения), третьи − за счет устранения зазора
, вторые – за счет изменения температуры (температурные
напряжения), третьи − за счет устранения зазора ![]() (монтажные
напряжения).
(монтажные
напряжения).
В первом
случае, когда (![]() ), силовые напряжения
), силовые напряжения
![]() ,
, ![]() ,
, ![]() ,
,
т.е. первый
участок стержня растягивается, а второй сжимается.
Во втором
случае, когда действует только температура (![]() )
)
![]() ,
, ![]() ,
, ![]() ,
,
т.е.
напряжения во всем стержне сжимающие.
В третьем
случае (![]() )
)
![]() ,
, ![]() ,
, ![]()
оба участка
растянуты. В этом случае стержень был растянут для
ликвидации зазора и закреплен.
Пример 8.
Сила ![]() передаётся через
абсолютно жёсткую плиту А
на сплошной стальной цилиндр 1
площадью поперечного сечения 15 см2 и полый медный цилиндр 2 площадью 20 см2. Сила
действует по оси обоих цилиндров (рис. 1).
передаётся через
абсолютно жёсткую плиту А
на сплошной стальной цилиндр 1
площадью поперечного сечения 15 см2 и полый медный цилиндр 2 площадью 20 см2. Сила
действует по оси обоих цилиндров (рис. 1).
Принять: Р = 45 кН; F1 = 15 см2; F2
= 20 см2; E1 = 2∙105
МПа; E2 = 1∙105 МПа; коэффициент
линейного расширения для стали ![]() = 1,2∙10 -5 1/град, для меди
= 1,2∙10 -5 1/град, для меди ![]() = 1,6∙10 -5 1/град.
= 1,6∙10 -5 1/град.
Требуется:
1. найти усилия в стальном N1 и медном цилиндрах N2; изменить температуру конструкции, чтобы усилия в стальном и медном цилиндрах были одинаковы N1=N2;
2. изменить температуру конструкции, чтобы
напряжения в стальном и медном цилиндрах были одинаковы ![]() .
.
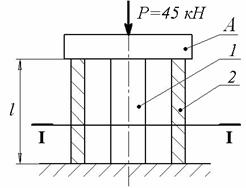
Рис. 1
Решение.
1. Определение усилий ![]() и
и ![]()
Сделаем
сечение ![]() и рассмотрим
равновесие верхней отсечённой части, действие отброшенной части заменим
усилиями
и рассмотрим
равновесие верхней отсечённой части, действие отброшенной части заменим
усилиями ![]() и
и ![]() (рис.
2).
(рис.
2).
Для данной
системы сил можно составить одно уравнение статики. (У=1). Число неизвестных
равно двум (R=2). Таким
образом, система один раз статически неопределима:
![]() .
.
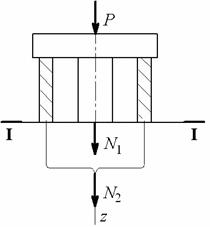
Рис. 2
Составим
уравнение равновесия
![]()
Рассмотрим
систему в деформированном состоянии (рис. 3) и составим уравнение совместности
перемещений.
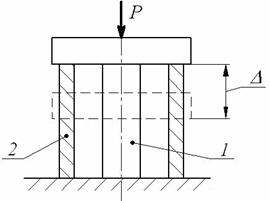
Рис. 3
Очевидно, что
![]() .
.
Выразим
деформацию цилиндров 1 и 2 через усилия
![]()
![]()
где учтено ![]() .
.
Тогда:
![]()
Следовательно:
![]()
Подставляя
полученное выражение ![]() , получим
, получим
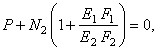
откуда
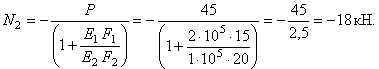
Тогда
![]()
Знак «минус» в
выражениях говорит о том, что усилия в цилиндрах будут сжимающими.
2. Изменение температуры конструкции ![]() , чтобы усилия в
цилиндрах стали одинаковыми
(
, чтобы усилия в
цилиндрах стали одинаковыми
(![]() )
)
Следовательно:
![]() .
.
В выражениях
для деформаций цилиндров нужно учесть влияние изменения температуры DТ.
Тогда
![]()
![]()
Отсюда:
![]()
или
![]()
откуда
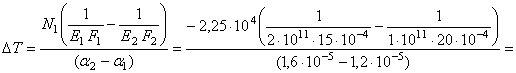
![]() .
.
Таким образом,
чтобы усилия в цилиндрах стали одинаковыми, конструкцию нужно нагреть на 9,4 °С.
3. Изменение температуры конструкции (![]() ), чтобы напряжения в цилиндрах стали
одинаковыми (
), чтобы напряжения в цилиндрах стали
одинаковыми (![]() )
)
Напряжения в
цилиндрах равны
![]()
Тогда с учетом
![]() получаем
получаем
![]() или
или ![]()
Тогда:
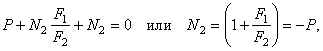
откуда
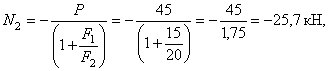
![]()
Выражения для
деформаций каждого из цилиндров
![]()
![]()
Тогда:
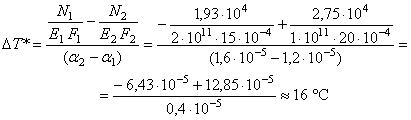
Таким образом,
чтобы напряжения в стальном и медном цилиндрах стали одинаковыми, конструкцию
нужно нагреть на 16 °С.
Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
