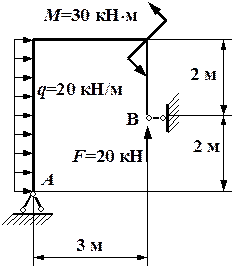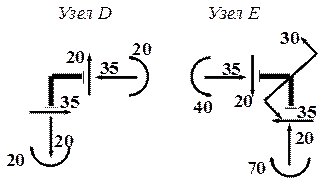Главная

Лекция 10. Статически определимые плоские рамы

Содержание

Стержневые системы и их классификация

Кинематический анализ стержневых систем

Расчет статически определимых рам

Рамы с жесткой заделкой

Рамы на двух шарнирных опорах

Рамы на двух опорах с промежуточным шарниром

Расчет комбинированных конструкций

Вопросы для самопроверки

Стержневые системы и их классификация

В сопротивлении материалов и в строительной механике при расчёте конструкций вместо них самих рассматриваются расчётные схемы или механические модели. В таких расчётных схемах стержни соединяются друг с другом связями в виде шарниров или жёстких узлов. Примерами простейших стержневых систем являются фермы (рис.10.1). Отличительной особенностью фермы является то, что нагрузку к ферме можно прикладывать в виде сосредоточенных сил только к узлам. Это объясняется тем, что стержни, из которых состоит ферма, испытывают деформацию растяжения или сжатия. Если нагрузку к ферме в виде сосредоточенной силы или распределенной нагрузки приложить непосредственно к стержню, соединяющему узлы, а не в узле, то такая нагрузка вызовет изгиб стержня, на который он не рассчитан. Внеузловое приложение нагрузки к ферме может привести к ее разрушению. Фермы получили широкое распространение как несущие конструкции на транспорте в мостовых сооружениях, в строительной индустрии для перекрытия больших пролетов при строительстве различных сооружений: промышленных цехов, концертных и торговых залов, ангаров, в машиностроении и т.д.

Усилия в фермах определяются методом сечений (вырезания узлов).

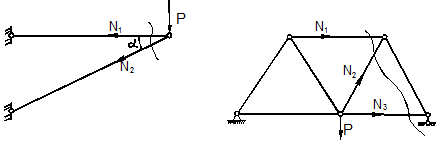
а) б)

Рис.10.1

Балками называются стержневые конструкции, испытывающие действие поперечных нагрузок, приложенных в виде сосредоточенных сил и моментов или распределенных нагрузок в любом сечении балки в пролете или на консоли (рис.10.2). Пролетом называется часть балки, расположенная между ее опорами. Консоль – это часть балки, выступающая за опору. Основной вид деформации, испытываемый балкой, является плоский поперечный изгиб. Однако балки могут испытывать другие виды деформации: косой изгиб (пространственный и плоский), изгиб с растяжением и сжатием, изгиб с кручением и т.д. Балки являются наиболее распространенными конструкциями, используемыми в строительстве и машиностроении.

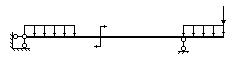
Рис.10.2. Балка

Если элементы-стержни соединяются с помощью жёстких узлов и испытывают в основном изгиб, то они называются рамами (рис 10.3).

Если балка лежит на нескольких опорах, то её называют неразрезной многопролётной балкой в отличие от многопролётных разрезных, в которых над опорами врезаны шарниры (рис.10.4), и она составляет ряд однопролётных статически неопределимых балок.

а) б) в) г)

Рис. 10.3

а) б)

Рис.10.4

Кривые стержни образуют арки (рис.10.5), которые в основном работают на сжатие и способны перекрывать большие пролёты.

а) б)

Рис.10.5

Кинематический анализ стержневых систем

Свойство систем изменять свою форму при отсутствии деформации называется их кинематической изменяемостью. При определении изменяемости или неизменяемости стержневой системы следует представить себе все её элементы абсолютно жёсткими. Каждую абсолютно жёсткую часть системы называют обычно диском.

В соответствии с классификацией по кинематическому признаку существуют три типа стержневых систем: геометрически изменяемые, геометрически неизменяемые и мгновенно изменяемые системы.

Геометрически изменяемыми называются такие стержневые системы, перемещение узлов которых возможно при отсутствии деформаций стержней системы. Сформулируем определение для геометрически изменяемой системы, используя понятие о связи и числе степеней свободы: геометрически изменяемой называется такая стержневая система, у которой число степеней свободы больше числа связей. В технике такие системы называют механизмами. Одним из примеров геометрически изменяемой системы является пантограф, используемый на транспорте для передачи тока от контактного провода к двигателю транспортного средства (рис.10.6).

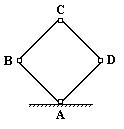
Рис.10.6. Пример геометрически изменяемой

системы в виде пантографа

Шарниры в точках А, В, С и D пантографа позволяют менять его конфигурацию в зависимости от необходимости. При этом прямые углы, образуемые элементами пантографа, изменяются, а деформации стержней пантографа не возникают.

Другим примером геометрически изменяемой системы является кривошипно-шатунный механизм (рис.10.7).

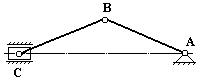
Рис.10.7. Пример геометрически изменяемой системы в виде

кривошипно-шатунного механизма

Кривошип АВ, вращаясь вокруг точки А, приводит в движение шатун ВС и вместе с ним ползун С. Если в точке В механизма приложить вертикальную силу, то ползун переместится и угол АВС изменит свою величину без возникновения деформаций в шатуне и кривошипе. Если искусственным образом ограничить перемещение ползуна С, то изображенная на рис.10.7 система перестанет быть геометрически изменяемой. Следует отметить, что геометрически изменяемые системы нельзя использовать в качестве несущих конструкций.

Геометрически неизменяемыми называются стержневые системы, перемещение узлов которых происходит только за счет деформации стержней системы или за счет смещения опор конструкции. В геометрически неизменяемой системе число степеней свободы всегда или равно числу связей или меньше числа связей. В геометрически неизменяемую систему можно превратить пантограф, изображенный на рис.10.6, если соединить узлы пантографа А и С жестким стержнем (рис.10.8).

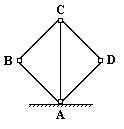
Рис.10.8. Пример геометрически неизменяемой системы

Теперь, чтобы изменить прямые углы СВА или CDA системы, нужно преодолеть сопротивление стержней системы и вызвать их деформацию.

В геометрически неизменяемую систему можно превратить и кривошипно-шатунный механизм. Для этого, как это отмечалось выше, необходимо ограничить перемещение ползуна С в горизонтальном направлении. В этом случае при приложении в узле вертикальной силы изменение угла АВС произойдет только в результате деформации элементов АВ и ВС.

Следует отметить, что в качестве несущих конструкций в технике всегда используются только геометрически неизменяемые системы.

С кинематической точки зрения мгновенно изменяемыми называются такие стержневые системы, которые допускают бесконечно малые перемещения узлов системы без деформации ее элементов. С этой точки зрения эти стержневые системы похожи на геометрически изменяемые. Но в отличие от геометрически изменяемых систем в мгновенно изменяемых системах при бесконечно малых перемещениях узлов возникают бесконечно большие усилия и напряжения в стержнях, что приводит к мгновенному разрушению конструкции. Покажем это на примере стержневой системы, состоящей из двух горизонтально расположенных стержней, соединенных в узле В шарниром (рис.10.9).

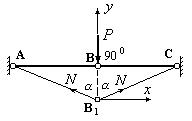
Рис.10.9. Пример мгновенно изменяемой стержневой системы

Пусть под действием силы P точка В системы сместилась вниз на бесконечно малую величину и система заняла положение АB₁С. В силу симметрии усилия в стержнях системы А B₁ и С B₁ будут одинаковыми и равными N. Поместим начало координат в точку B₁ и составим уравнение равновесия на ось y. Получим:

Из уравнения (1) следует:

Если учесть, что перемещение точки В было бесконечно малым, угол 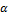практически не изменился и остался равным 90°. При 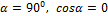и, следовательно, из уравнения (2) усилие 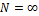. Таким образом, при бесконечно малом перемещении узла В в системе возникают бесконечно большие усилия.

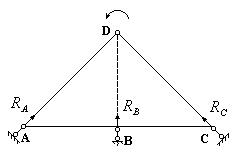
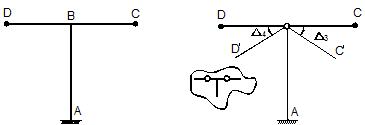
К числу мгновенно изменяемых стержневых систем можно отнести также систему, реакции опор которой сходятся в одной точке (рис.10.10). При таком расположении опор возможен бесконечно малый поворот балки вокруг точки D. Это может вызвать бесконечно большие усилия в опорах и разрушение последних.

Рис.10.10. Пример мгновенно изменяемой системы

Следует отметить, что мгновенно изменяемые системы нельзя использовать в качестве несущих конструкций.

Для выяснения вопроса о геометрической изменяемости или неизменяемости стержневых систем проводится их кинематический анализ.

Степенью свободы твёрдого тела, в т.ч. стержня, называется число независимых перемещений или координат N, определяющих его положение в пространстве или на плоскости.

Свободная точка на плоскости имеет две степени свободы – координаты x и y (рис.10.11).

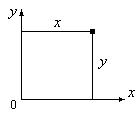
Рис.10.11

Свободная точка в пространстве имеет три степени свободы – координаты x, y и z (рис.10.12).

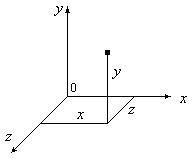
Рис.10.12

Свободное тело на плоскости обладает тремя степенями свободы – две координаты произвольной точки, принадлежащей прямой линии АВ, проведенной в теле, и угол поворота прямой линии АВ относительно одной из осей координат (рис.10.13).

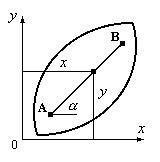
Рис.10.13

Стержень в плоскости обладает тремя степенями свободы (N = 3). Его положение можно определить с помощью трёх перемещений (рис.10.14,а).

Свободное тело в пространстве обладает шестью степенями свободы – тремя координатами произвольной точки, принадлежащей прямой линии, проведенной в теле, и тремя углами поворота этой линии относительно осей координат.

Устройство, уничтожающее степень свободы, называется связью. В зависимости от соотношения между числом степеней свободы и числом связей, накладываемых на тело, различают еще несколько классификаций стержневых систем.

Связь, которая лишает тело одной степени свободы, называется простой. Один опорный стерженёк (например, каток) представляет собой такую одну простую связь (рис.10.14,б). Он лишает стержень одного вертикального независимого перемещения . Закреплённый стержень имеет в плоскости две степени свободы N = 2.

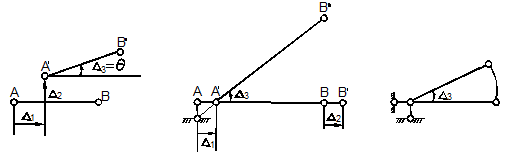
а) б) в)

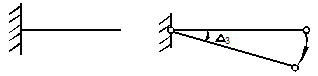
г) д)

Рис.10.14

На рис.10.14,в левый конец стержня закреплён с помощью двух опорных стерженьков (неподвижный шарнир), т.е. двух простых связей , он лишает тело двух независимых перемещений и и разрешает только поворот . Степень свободы так закреплённого стержня N = 1.

Если левый конец стержня защемить (рис.10.14, г), то он теряет возможность к перемещениям в плоскости. Его степень свободы N = 0. В этом случае будем говорить, что на стержень наложены три простые связи.

Освободим теперь стержень от одной простой связи, врезав в защемление на левом его конце шарнир (рис.10.14, д). Стержень получает возможность к вращению, и его положение определяется угловым перемещением . Его степень свободы стала снова N =1.

Пусть мы имеем простейшие рамы (рис.10.15) Заменим жёсткий узел В в первой из них (рис.10.15,а) шарниром. Мы можем отметить, что внутренний шарнир В снимает одну простую связь при соединении двух стержней. Если в узле В сходятся три стержня и мы врезаем в их соединение шарнир, то он снимает две простые связи, т.е. на единицу меньше числа сходящихся в раме стержней. Если соединяется m стержней (m>3) , то при врезании шарнира освободится (m-1) простая связь.

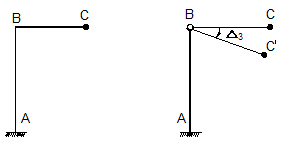
а) б)

Рис.10.15

Учитывая изложенное выше, мы можем степень свободы стержневой системы вычислить по формуле П.Л.Чебышева:

где Д – число неизменных жёстких частей стержневой конструкции, обладающих тремя степенями свободы; Ш₀ – число простых шарниров; С₀ – число опорных стержней (простых связей).

Для определения числа Д следует предварительно отбросить все внутренние шарниры и опорные связи, а для определения Ш₀ – все опоры.

Для шарнирно-стержневых систем (ферм) степень свободы может быть определена по более простой формуле:

где У – число узлов фермы, С = Д – число внутренних стержней фермы, С₀ – число опорных стержней (простых внешних связей).

На рис 10.16,а изображена стержневая система у которой

Система кинематически неизменяемая.

Врежем в данную стержневую систему два шарнира в узлах Е, Н (рис.10.16,б,в).

Тогда у системы будет

Следовательно система имеет две степени свободы.

Два независимых перемещения системы и показаны на рис.10.16,б,в.

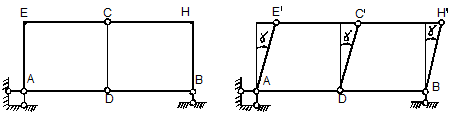
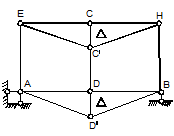
а) б) в)

Рис.10.16

В заключение отметим, что число простых связей, превращающих стержневую систему в неизменяемую, называется необходимым числом связей для образования стержневой конструкции.

Расчет статически определимых рам

Статически определимыми системами называются стержневые системы, для определения реакций опор в которых достаточно уравнений равновесия. С точки зрения соотношения числа связей и числа степеней свободы статически определимыми называются стержневые системы, число степеней свободы которых равно числу связей, накладываемых на систему. Примеры статически определимых балок и рам приведены на рис.10.17.

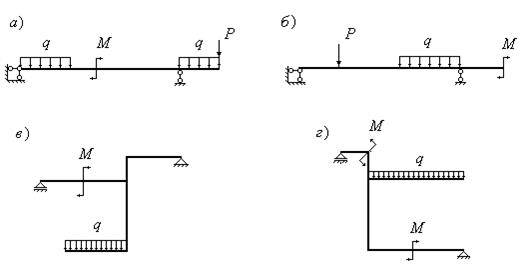
Рис.10.17

Варианты опор принимаются в виде отдельных стержней (рис. 10.17,а,б) и в виде треугольников (рис.10.17,в,г). На рис.10.17,а левая опора, состоит из двух стержней, ограничивающих перемещение балки в вертикальной и горизонтальном направлении. Такая опора называется шарнирно неподвижной и соответствует правой опоре на рис.10.17,в.

Некоторые стержневые системы, обладая лишними внешними связями, тем не менее являются статически определимыми системами. Пример такой статически определимой балки приведен на рис.10.18,а.

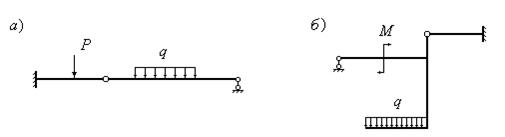
Рис.10.18

Балка имеет один внутренний шарнир. Реакции опор таких стержневых систем определяются с использованием только уравнений равновесия и, следовательно, эти системы являются статически определимыми. Методика определения реакций в таких системах приводится в разделе “Статика” в теоретической механике. Еще один пример внутренне статически определимой рамы приведен на рис. 10.18,б.

Статически определимая рама – конструкция, состоящая из нескольких изгибаемых стержней, закрепленных так, что опорные реакции и внутренние усилия можно найти с помощью уравнений статики. Чаще всего стержни рамы соединены между собой жестким образом, так, что в процессе деформации угол между стержнями не меняется. Мы будем рассматривать только плоские рамы, стержни которых расположены под углом 90°. Вертикальные стержни рамы принято называть стойками, горизонтальные – ригелями. Конструкция рамы позволяет прикладывать нагрузку в любом сечении рамы, как в узлах, так и вне узлов. Стержни рамы могут испытывать те же деформации, что и балочные конструкции. Рамные системы получили широкое распространение в промышленном и гражданском строительстве, в машиностроении, на транспорте, в авиа- и судостроении и т.д. В стержнях плоских рам возникают три внутренних усилия: продольная и поперечная силы и изгибающий момент.

Первым этапом расчета является определение усилий в опорных связях, т. е. реакций опор.

Внутренние усилия в рамах определяются методом сечений, и порядок их нахождения тот же, что и для балок. Из шести внутренних силовых факторов в сечениях плоской рамы в общем случае возникают три: продольная сила N; поперечная сила Q; изгибающий момент M. Напомним, что согласно методу сечений:

- продольная сила N равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось стержня;

- поперечная сила Q равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось, перпендикулярную оси стержня;

- изгибающий момент M равен сумме моментов всех сил, действующих с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения.

Правила знаков для продольной и поперечной сил те же, что и раньше: растягивающая продольная сила положительна, поперечная сила положительна, если она обходит сечение по ходу часовой стрелки. Правило знаков для изгибающего момента в рамах следующее: момент считается положительным, если он изгибает стержень рамы выпуклостью вовнутрь (для некоторых рам невозможно определить, где внешняя часть рамы, а где внутренняя. В этом случае знак изгибающего момента не определяется и эпюра изгибающих моментов строится со стороны растянутых волокон без знака).

На эпюрах N и Q положительные значения принято откладывать снаружи, на эпюре М – внутри – со стороны растянутых волокон.

От действия трех внутренних усилий в стержнях рамы возникают напряжения: нормальные и касательные. Нормальные напряжения определяются как сумма напряжений от продольной силы (N/A) и от изгибающего момента по формуле

Касательные напряжения находят по формуле Журавского

Перемещения точек оси рамы определяются, как правило, методом Максвелла – Мора по формуле

Заметим, что произвольная точка оси рамы в отличие от точки оси балки может перемещаться не только по вертикали, но и по горизонтали. Будем обозначать линейные перемещения точек оси рамы буквой , отмечая направление перемещения индексом сверху: и . Углы поворота сечений рамы, как и балок, обозначаем буквой .

В данном разделе ограничимся рассмотрением простейших статически определимых рам трех видов:

1) с жесткой заделкой;

2) на двух шарнирных опорах (неподвижной и подвижной);

3) на двух шарнирно неподвижных опорах с простым промежуточным шарниром.

Рамы с жесткой заделкой

Пример 1.

Рассмотрим жесткозащемленную плоскую раму (рис.10.19,а). В жесткой заделке рамы в общем случае нагружения возникают три опорные реакции: две силы (и ) и опорный момент (). Для построения эпюр определение этих реакций не является безусловной необходимостью: расчет, как и в случае жесткозащемленной балки, можно вести от свободного конца, то есть всякий раз так выбирать отсеченную часть для рассматриваемого сечения, чтобы в нее не попадала опора с неизвестными опорными реакциями. Тем не менее, иногда целесообразно вычислить опорные реакции. Это позволяет проверить построение эпюр или облегчить их построение. Для вычисления реакций в жесткозащемленной раме используются три условия равновесия:

Построим эпюры для рассматриваемой рамы, не вычисляя опорные реакции.

Методика построения эпюр аналогична ранее рассмотренной для балок, т.е. сначала необходимо наметить характерные сечения. В дополнение к ранее указанным, в рамах характерными являются также сечения, расположенные бесконечно близко к жесткому узлу на всех элементах, сходящихся в этом узле.

Построение эпюры . Следуя установленным правилам, в рассматриваемой раме можно выделить 8 характерных сечений. Продольная сила в любом из них численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня. При этом следует учитывать, что положение продольной оси будет изменяться в зависимости от того, чему принадлежит рассматриваемое сечение - стойкам или ригелю.

Построение эпюры . Поперечная скила в любом сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную ось рамы. Положение поперечной оси также будет изменяться в зависимости от принадлежности данного сечения стойкам или ригелю. С учетом правила знаков, двигаясь от свободного конца к жесткой заделке, получим для :

(проекция пары М на любую ось равна нулю);

Необходимо обратить внимание на тот факт, что , т.е. что поперечная сила в верхних сечениях противоположных стоек от действия силы, приложенной к правой стойке (при заделке, расположенной слева, и наоборот) имеет противоположные знаки. Отчасти это можно объяснить противоположными направлениями оси y для сечений 4 и 7, но более строгое обоснование указанного равенства будет дано ниже.

Построение эпюры . Изгибающий момент в любом сечении численно равен алгебраической сумме моментов всех нагрузок, приложенных по одну сторону от рассматриваемого сечения, относительно этого сечения (более строго: относительно оси x этого сечения). Обратим внимание на два важных замечания:

1) составляющая момента от действия сосредоточенного момента М всегда одинакова и равна М;

2) под плечом силы всегда понимается длина перпендикуляра, опущенного из центра тяжести данного сечения на линию действия силы. Это означает, что, например, плечо силы F для сечений 4-7 одинаково и равно 3 м.

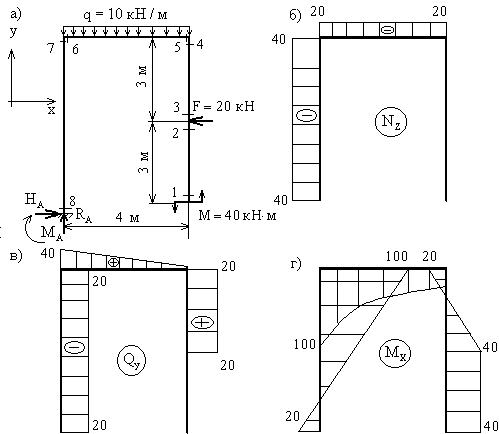
Рис.10.19

Таким образом, для сечений 1-8 получим:

(сжатым является правое волокно в сечениях 1-3, поэтому ордината отложена вправо от оси стойки);

(знаки "+" и "-" здесь имеют относительный характер; результирующий момент сжимает левые волокна в сечении 4 и нижние волокна в сечении 5, поэтому ордината "20" откладывается соответственно влево и вниз);

(сжаты нижние волокна);

(сжаты правые волокна);

(сжаты левые волокна).

Между в плоских рамах сохраняются те же зависимости, что и в балках, а именно:

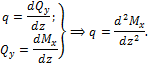
Из этого следует, что правила контроля эпюр и остаются теми же, что и для балок.

Эпюры в плоских рамах строятся наиболее просто и при отсутствии нагрузок, распределенных вдоль стержней, представляют собой графически отрезки прямых, параллельные осям стержней (или совпадают с ними при ).

Если проанализировать процесс построения эпюр (рис.10.19,б-г), то очевидно, что наиболее "сложно" вычислять ординаты в сечениях стержня, примыкающего к заделке (на рис.10.19,б-г это сечения 7 и 8). Как уже отмечалось, с этой целью иногда вычисляют реакции и момент .

При принятом для всей рамы направлении осей z,y (рис.10.19,а) уравнения равновесия имеют вид:

Полученный для каждой из величин знак "+" говорит, что направления их были выбраны правильно.

После вычисления опорных реакций значения величин в сечениях 7 и 8 (как, впрочем, и в любом другом) можно вычислять, двигаясь от жесткой заделки к свободному концу.

Например, для сечений 7 и 8:

(знак "-" указывает на сжатие в этих сечениях с силой );

(т.к. реакция стремится повернуть каждое из этих сечений против часовой стрелки.)

При сравнении величины с ранее полученной величиной видно, что

, о чем уже говорилось выше.

(сжаты левые волокна стойки);

(сжаты правые волокна стойки).

Разумеется, результаты получаемые для любого сечения при движении от свободного конца к жесткой заделке и при движении в обратном направлении одинаковы.

Пример 2.

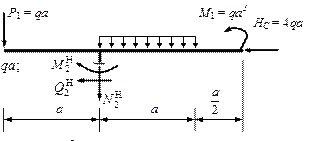
Для рамы, жестко защемленной одним концом (рис.10.20), построить эпюры N_z, Q_y и M_x.

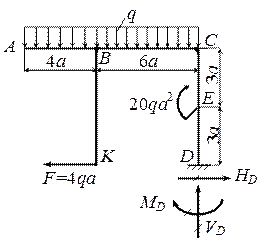
Рис.10.20

Решение.

1. Определение опорных реакций:

2. Построение эпюр N_z, Q_y, M_x (рис.10.21).

Э п ю р а N_z. Стойка CD сжимается силой N_CD = -V_D = -10qa, а ригель ВС растягивается силой N_BC = F = 4qa. В остальных стержнях продольной силы нет.

Э п ю р а Q_y. На участках ВК и CD поперечная сила постоянна Q_BK = F =4qa, Q_CD = -H_D = -4qa, а в ригеле АС изменяется по линейному закону от Q_A = 0 до Q_CB = -q10a = -10qa.

Рис. 10.21

Э п ю р а М_х. В стойке ВК момент изменяется по линейному закону от М_К = 0 до М_ВК = 4qa6a = 24qa² (растяжение с внутренней стороны контура). В стойке CD также имеем линейный закон со скачком в сечении Е, где приложена пара сил 20qa². Сосредоточенный момент вызывает растяжение с правой стороны стойки при движении от точки D к точке С, поэтому и скачок на эпюре будет вправо на величину приложенного момента. Вычисляем

M_ED = -M_D + H_D3a = -30qa² + 4qa3a = -18qa²,

M_EC = M_ED - M = -18qa² - 20qa² = -38qa²,

M_CE = -M_D - M + H_D3= -26qa² и строим эпюру в стойке CD. В узле С нет внешней пары сил, поэтому M_CB = M_CE = -26qa². В ригеле АС, нагруженном погонной нагрузкой q, изгибающий момент изменяется по квадратичному закону. В точке А нет внешней пары сил, поэтому М_А = 0. Вычисляем

M_BA = -q4a2a = -8qa² (растяжение сверху),

M_BС = -q4a2a + F6a = 16qa² (растяжение снизу) и строим параболу, обращенную выпуклостью вниз (в направлении погонной нагрузки q).

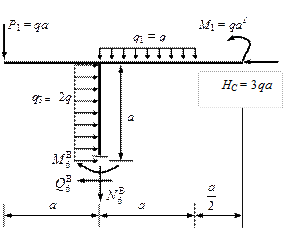
Пример 3.

Произвести расчет плоской рамы и подобрать круглое сечение диаметром d. Материал стержня Сталь 30.

Исходные данные для расчета плоской рамы представлены на рис. 10.21.1.

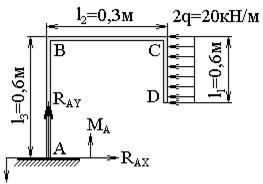
Рис.10.21.1

Решение.

1. Определим реакции, возникающие в заделке:

2. Для построения эпюр внутренних силовых факторов рассмотрим три произвольных сечения на участках АВ, ВС и CD (рис. 10.21.2).

На участке АВ (0z₁l₃) (рис. 10.21.2,а):

На участке ВС (0z₂l₂) (рис. 10.21.2,б):

На участке CD (0z₃l₁) (рис. 10.21.2,в):

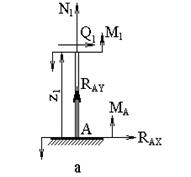
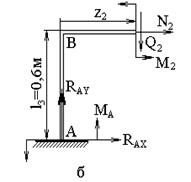
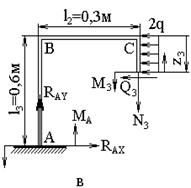
Рис.10.21.2

По полученным данным строим эпюры продольной, перерезывающей силы и изгибающего момента (рис. 10.21.3).

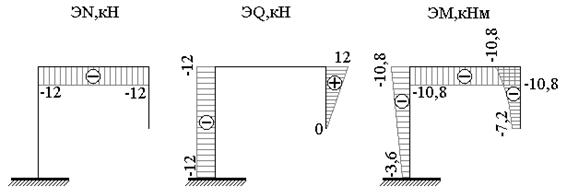
Рис.10.21.3

3. Расчет на прочность.

Рассчитаем диаметр стержней, исходя из условия прочности, при этом М_max=10,8 кНм, материал стержня Сталь 30, допускаемые напряжения

где n – коэффициент запаса, тогда диаметр стержня:

Примем (из ряда Ra20 по ГОСТ 6636-69) d=80 мм.

Рамы на двух шарнирных опорах

В дальнейшем для краткости будем говорить "шарнирная рама", имея в виду ее статическую определимость и отсутствие промежуточных шарниров.

Пример 4.

Рассмотрим раму той же конфигурации, размеров и с теми же нагрузками, что и в предыдущем примере 1, но с шарнирным опиранием (рис. 10.22, а).

Здесь также имеем 8 характерных сечений, но для построения эпюр необходимо вычислить сначала опорные реакции, т.к. ни для одного из сечений нельзя выбрать отсеченную часть так, чтобы избежать попадания в нее опоры с неизвестной реакцией.

Для определения опорных реакций в плоских шарнирных рамах используются следующие уравнения равновесия:

Первое уравнение равновесия используется в том из двух приведенных вариантов, который будет содержать одну неизвестную опорную реакцию.

Так, в рассматриваемом примере этим условием будет , которое будет содержать неизвестную реакцию H_A (в то время как условие содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие .

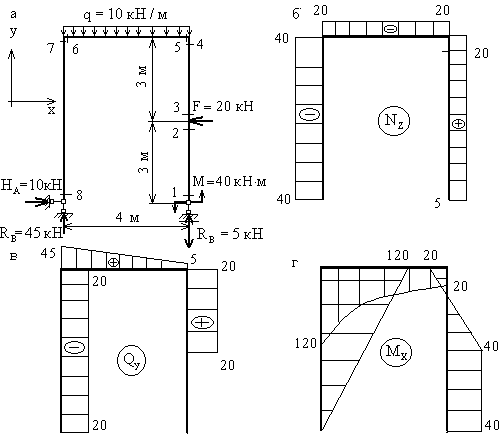
Рис.10.22

Второе и третье уравнения равновесия () - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения (иногда - с нулевым плечом).

В качестве проверки вычисленных реакций используется условие, противоположное первому, то есть или .

Построение эпюр N_z, Q_y и M_x в шарнирных рамах выполняется так же, как и в защемленных, но "с меньшими затратами", так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.

Вычислим реакции опор рамы (рис.10.22,а)

Уравнения статики:

Знак "-", полученный при вычислении реакции R_A, говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку:

то есть реакции опор вычислены правильно.

Построение эпюры N_z.

Двигаясь по оси рамы от сечения 1 к сечению 6, получим:

N_z1 = N_z2 = N_z3 = N_z4 = R_B = 5 кН,

N_z5 = N_z6 = - F = - 45 кН.

Для сечений 7 и 8 проще рассматривать отсеченную часть, продвигаясь от опоры А к сечению 7:

N_z8 = N_z7 = - R_A = - 45 кН.

Этот же результат получим из рассмотрения отсеченной части 1-6:

N_z7 = N_z8 = - R_B - q4 = - 45 кН.

По вычисленным значениям строим эпюру N_z (рис. 10.22,б)

Построение эпюры Q_y.

Из рассмотрения отсеченной части 1-5:

Q_y1 = Q_y2 = 0,

Q_y3 = Q_y4 = F = 20 кН,

Q_y1 = R_A = 5 кН.

Из рассмотрения отсеченной части 8-6:

Q_y8 = Q_y7 = - H_A = - 20 кН,

Q_y1 = R_A = 45 кН.

Эпюра Q_y, построенная по вычисленным значениям, показана на рис. 10.22,в.

Построение эпюры M_x.

Из рассмотрения отсеченной части 1-5:

M_x1 = M_x2 = M = 40 кНм (сжаты правые волокна стойки);

M_x3 = M_x2 = 40 кНм (плечо силы F равно нулю);

M_x4 = M_x5 = M - F3 = - 20 кНм (сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);

Из рассмотрения отсеченной части 8 -6:

M_x8 = 0,

M_x7 = M_x6 = H_A6 = 120 кНм

(сжаты правые волокна стойки и нижние волокна ригеля в сечениях 7 и 6 соответственно).

Эпюра M_x показана на рис. 10.22,г.

Пример 5.

Рассмотрим шарнирную раму более сложной конфигурации (рис.10.23, а).

Здесь необходимо рассматривать 10 характерных сечений для построения эпюр N_z, Q_y и M_x. Сечения 1-6 расположены на ригеле слева направо, а сечения 7-10 - на стойке сверху вниз. Как и в предыдущем примере, указанное расположение характерных сечений является безусловно необходимым, а их нумерация - произвольной.

Уравнения статики для вычисления опорных реакций имеют вид:

Проверка вычисления опорных реакций:

При построении эпюр N_z, Q_y и M_x целесообразно выбирать отсеченную часть, продвигаясь к центральному узлу рамы с четырех сторон, т.к. в этом случае определение внутренних силовых факторов в каждом из характерных сечений осуществляется наиболее просто.

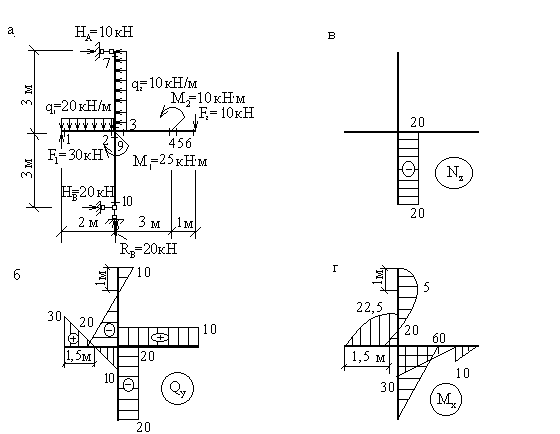
Рис.10.23

Построение эпюр N_z, Q_y и M_x .

Из рассмотрения левой относительно центрального узла отсеченной части (сечения 1-2):

(сжаты верхние волокна).

Из рассмотрения правой отсеченной части (сечения 3-6):

Из рассмотрения верхней относительно центрального узла отсеченной части (сечения 7-8):

Из рассмотрения нижней отсеченной части (сечения 9-10):

Характер эпюры Q_y на участках рамы с распределенными нагрузками q₁ и q₂, а именно, наличие пересечений эпюры с осью рамы, говорит о том, что в этих точках момент M_x принимает экстремальные значения. Определение положений точек пересечения (т.е. тех точек, где Q_y = 0) выполняется так же, как и в балках.

Вычислим экстремальные значения момента M_x.

На участках под распределенной нагрузкой q₁:

(сжаты верхние волокна).

На участке с распределенной нагрузкой q₂:

(сжаты правые волокна).

Эпюры N_z, Q_y и M_x показаны на рис.10.23,б,в,г.

Пример 6.

Построить эпюры продольной и поперечной сил, а также изгибающего момента для рамы, приведенной на рис. 10.24.

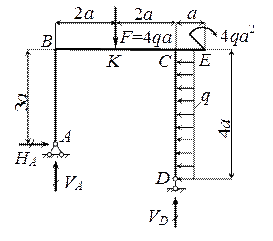
Рис. 10.24

Решение.

1. Определение опорных реакций.

Составляем уравнения равновесия:

, Н_А = 4qa;

, V_D4a - 4qa² + q4aa - F4a = 0, откуда V_D = 2qa;

, -V_A4a - Н_Аa - 4qa² + q4aa + Fa = 0, откуда V_A = 2qa.

Проверка:

2. Построение эпюр N_z, Q_y, M_x (рис.10.16).

Э п ю р а N_z. В стойках: N_AB = -V_A = -2qa, N_CD = -V_D = -2qa.

Ригель ВС сжимается силой Н_А, поэтому N_DC = -H_A = -4qa. На консоли СЕ продольная сила отсутствует, т.е. N_СЕ = 0.

Э п ю р а Q_y. На участках АВ, ВС и СЕ нет погонной нагрузки, поэтому поперечная сила постоянна. В стойке CD поперечная сила изменяется по линейному закону. Вычисляем поперечную силу в характерных точках Q_A = -H_A = - 4qa, Q_BK = V_A = 2qa, Q_CK = Q_BK - F = -2qa, Q_CD = H_A = 4qa, Q_D = 0, Q_E = 0 и строим эпюру Q_y.

Э п ю р а М_х. В стойке АВ изгибающий момент изменяется по линейному закону от М_А = 0 до М_В = -Н_Аa = -12qa² (растяжение с наружной стороны контура). Аналогичный характер имеет эпюра М_х на участках ВК и КС.

Находим М_К = V_A2a - Н_А3a = -8qa² растяжение снаружи и М_СК = V_A4a - Н_А3a - F2a = -12qa².

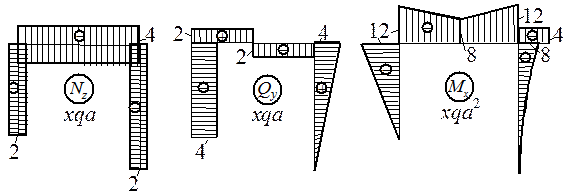
Рис. 10.25

На консоли СЕ изгибающий момент постоянен (Q_y = 0) и равен М_СЕ = -4qa² (растяжение сверху). В стойке CD, загруженной равномерно распределенной нагрузкой, момент изменяется по закону квадратной параболы, обращенной выпуклостью в сторону погонной нагрузки (влево). По условию загружения на опоре D M_D = 0, а в сечении С изгибающий момент вычисляем как сумму моментов всех сил, расположенных ниже этого сечения M_CD = -q4a2a = -8qa² (растяжение с наружной стороны контура). По двум точкам (С и D) приближенно строим параболу.

Эпюры N_z, Q_y и M_x показаны на рис.10.25.

Пример 7.

Рассмотрим раму, показанную на рис.10.26, и определим в ней внутренние усилия, то есть построим эпюры N, Q и М.

Рис.10.26

Решение.

Найдем три опорные реакции, используя три уравнения статики. Желательно составлять такие уравнения, чтобы в каждое из них входила бы только одна неизвестная реакция. В данном примере это такие уравнения (предполагаемые направления реакций показаны на рис. 10.27, а):

Сумма проекций сил на вертикальную ось равна 0;

Для проверки используем уравнение "сумма проекций сил на горизонтальную ось равна нулю":

Находим внутренние усилия, используя метод сечений. Рама имеет три участка. Заметим, что если для балки границей между участками считалось сечение, где появлялся новый силовой фактор, то для рам границей между участками является также и узел, где соединяются соседние стержни рамы (стойка и ригель). Рассечем стержни рамы на трех участках и выберем начало отсчета х на каждом участке (удобно начало отсчета выбирать в начале участка – рис. 10.27, а).

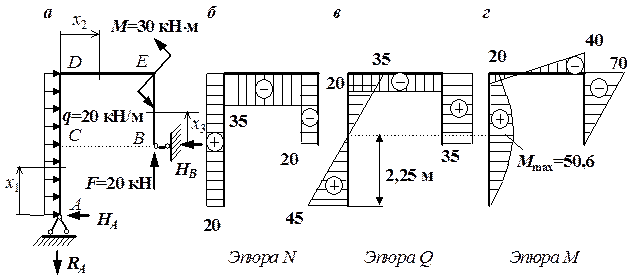
Рис.10.27

Запишем выражения для продольной, поперечной сил и изгибающего момента на каждом участке, используя вышеприведенные определения этих усилий и правила знаков для них:

участок 1: м;

участок 2: м;

участок 3: м;

Строим эпюры усилий, используя написанные выражения (рис. 10.27, б, в, г). Значение максимального момента определяем так же, как в балках.

Проверку правильности построения эпюр в рамах производим, проверяя равновесие узлов. Для этого вырезаем узлы (в рассматриваемой раме их два: D и E) и прикладываем к сечениям, примыкающим к узлам, все внутренние усилия согласно построенным эпюрам. Направление усилий должно соответствовать их знакам. На рис.10.28 показаны вырезанные из рамы узлы D и E вместе с действующими в сечениях, примыкающих к узлам, внутренними усилиями. Видно, что узлы находятся в равновесии. Из условия равновесия узлов следует, что, если в узле не приложена внешняя пара сил (узел D), то изгибающие моменты в сечениях, примыкающих к узлу, обязательно одинаковы. То есть, зная изгибающий момент в угловой точке для стойки, можно получить графически ординату М в угловой точке для ригеля, проведя циркулем дугу из вершины угла, как из центра. Если в узле действует сосредоточенная пара сил, то значения изгибающих моментов в примыкающих сечениях отличаются на величину этой пары.

Рис.10.28

Пример 8.

Для заданной рамы (рис 10.29, а) построить эпюры продольных сил; поперечных сил; изгибающих моментов. Провести подбор квадратного сечения из условия прочности МПа, для опасного сечения рамы. a=0,4 м; M=20 кНм; P=10 кн; q=40 кН/м.

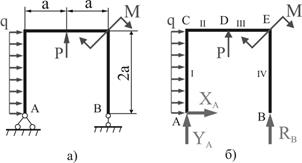
Рис. 10.29

Решение.

Ось рамы представляет собой ломаную линию, однако каждый прямолинейный участок ее можно рассматривать как балку. Поэтому, чтобы построить какую либо эпюру для рамы, нужно построить ее для каждой отдельной балки, входящей в состав рамы. В отличие от обыкновенных балок в сечениях стержней рамы, кроме изгибающих моментов М и поперечных сил Q, обычно действуют еще и продольные силы N. Следовательно, для рам нужно строить эпюры N, Q и M.

Для N и Q сохраняются ранее принятые правила знаков:

N>0, если продольные силы вызывают растяжение;

Q>0, если ее векторы стремятся вращать части рассеченной рамы (относительно точек, близких к сечению) по часовой стрелке.

Для изгибающих моментов специального правила знаков не устанавливают, а при составлении выражений для M(x) принимают по собственному усмотрению какой либо момент положительным.

Выражения для N(x), Q(x), и M(x) записывают очень редко — главным образом для тех участков, где действует распределенная нагрузка. Чаще всего просто вычисляют значения N, Q и M в характерных сечениях (на границах участков и в экстремальных точках), а затем проводят линии эпюр, учитывая особенности построения этих эпюр.

Ординаты эпюр, как и всегда, откладываем перпендикулярно к оси рамы, причем положительные ординаты N и Q с внешней стороны рамы, а отрицательные — с внутренней (если, конечно, рама такой конфигурации, что можно различить ее наружную и внутреннюю стороны). Эпюры М условимся и для рам строить на сжатых волокнах.

1) Нахождение опорных реакций.

Так как рама имеет более одной опоры, то прежде чем приступить к построению эпюр, нужно обычными методами статики найти опорные реакции (рис. 10.29, б).

Для проверки правильности определения реакций опор составим уравнение моментов относительно точки приложения силы P:

2) Эпюра «N»

Чтобы построить эпюру «N», нужно спроецировать силы, приложенные к части рамы, лежащих по одну сторону от сечения, на ось стержня.

На участке AC: (растяжение).

На участке CD (рассматриваем правую часть):

На участке DE (рассматриваем правую часть):

На участке BE: (сжатие).

По этим данным строим эпюру «N» (рис. 10.30, а)

3) Эпюра «Q»

В сечении A стержня AC (т. е. в сечении I, бесконечно близком к A) имеем

В сечении C стержня AC

Для любого сечения на участке CD сумма проекций лежащих справа сил на сечение одинакова и равна Y_A

Для любого сечения на участке DE сумма проекций лежащих справа сил на сечение одинакова, равна R_B и дает отрицательную величину, т. к. сила R_B стремится повернуть сечение на III участке против часовой стрелки:

Для любого сечения на участке BE сумма проекций нижележащих сил на сечение равна нулю:

Эпюра «Q» представлена двумя прямоугольниками на горизонтальной части рамы и треугольником на стойке AC (рис.10.30, б)

4) Эпюра «M»

Для построения эпюры «M» будем вычислять величины изгибающих моментов в характерных сечениях A, C, D и B.

Очевидно, что в точке A:

Очевидно и то, что в любом сечении стержня BE:

В сечении C стержня AC (т. е. в сечении I, бесконечно близком к C) имеем

Знак плюс в данном выражении мы выбирали, предполагая, что сжаты правые волокна. Получившийся знак минус при подстановке значения X_A говорит о том, что в сечении C стержня AC будут сжаты волокна слева. Поэтому на эпюре «M» из точки C откладываем влево координату, равную 12,8 кНм.

Поперечная сила на участке AC не меняет знак (не будет экстремальных значений на эпюре изгибающих моментов), поэтому для построения эпюры изгибающих моментов на данном участке проводим кривую второго порядка ac выпуклостью навстречу направлению распределенной нагрузки q (выпуклостью влево). Учитывая, что поперечная сила в точке C , касательная к эпюре моментов в этой точке параллельна оси участка (рис. 10.30, в).

В сечении E стержня DE (в сечении III, бесконечно близком к точке E) изгибающий момент будет равен внешнему моменту M:

кНм.

Под действием момента M сжимаются нижние волокна, поэтому значение кНм будем откладывать вниз.

В сечении D стержня DE (в сечении III, бесконечно близком к точке D) изгибающий момент будет равен

кНм.

Положительный момент в сечении создавался внешним моментом M, который сжимает нижние волокна. Поэтому положительное значение 5,6 кНм откладываем из точки D вниз и проводим на эпюре «M» прямую de.

Так как в точке D отсутствует внешний сосредоточенный момент, в сечении D стержня CD имеем ту же величину изгибающего момента, что и для сечения D стержня DE:

кНм.

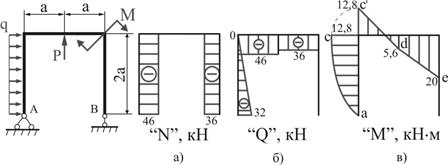
Рис. 10.30

В сечении C стержня CD (т. е. в сечении II, бесконечно близком к C), приняв, что положительный будет такой изгибающий момент, который вызывает сжатие нижних волокон, имеем такое же выражение момента, что и для сечения C стержня AC

кНм

Знак «минус» говорит о том, что в сечении С стержня CD сжаты верхние волокна. Откладываем вверх координату, равную 12,8 кНм и проводим на эпюре изгибающих моментов прямую

5) Подбор квадратного сечения.

По эпюре изгибающих моментов видно, что опасным будет являться сечение в точке E, для которого изгибающий момент равен M=20 кНм

Условие прочности:

где осевой момент сопротивления; для квадратного сечения

Сторона квадрата b определится по формуле

Принимаем величину b ближайшую большую, кратную пяти.

b=95 мм

Если кроме изгибающего момента в опасном сечении действует и продольная сила N, то сечение необходимо проверить с учетом нормальных напряжений от продольной силы по формуле

Если более чем на 5%, необходимо увеличить размер сечения и снова выполнить проверку с учетом нормальных напряжений от продольной силы.

Пример 9.

Для рамы, приведенной на рис.10.31, построить эпюры внутренних усилий: нормальных сил N, поперечных сил Q и изгибающих моментов М.

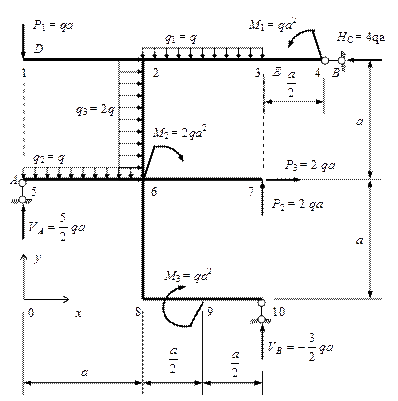
Рис.10.31

Решение.

1. Определяем опорные реакции.

Для определения реакции V_A составляем уравнение моментов относительно точки Е – точки где пересекаются реакции V_A и Н_с:, для реакции V_В - уравнение моментов относительно точки D (пересечение реакций V_В и Н_с), для реакции Н_с: - уравнение проекций на горизонтальную ось Х.

а)

б)

в)

Так как реакция V_В получилась со знаком минус, то реальное ее направление противоположно указанному на схеме рамы (рис. 10.31). Не меняя направление реакции на чертеже, в последующих расчетах подставляем отрицательное значение реакции.

Для проверки правильности определения вертикальных реакций используем уравнение проекций на вертикальную ось Y -

Уравнение равновесия удовлетворяется, вертикальные реакции определены верно.

2. Вычисляем значения внутренних усилий – нормальных N и поперечных Q сил и изгибающих моментов М.

Для определения внутренних сил проводим сечение, которое всегда разбивает простую раму на две части, вычерчиваем одну из частей (ту, при рассмотрении которой проще определить внутренние усилия), указываем на чертеже положительные направления внутренних усилий и определяем внутренние усилия из уравнений равновесия отсеченной части рамы.

Примечание. На концах стержней значения внутренних усилий всегда равны соответствующим внешним сосредоточенным силам (в том числе опорным реакциям), приложенным в этих точках рамы: продольным внешним силам (силам, действующим вдоль оси стержня) - для нормальных сил N; поперечным внешним силам (силам, действующим перпендикулярно оси стержня) - для поперечных сил Q; внешнему моменту - для изгибающих моментов М. При отсутствии внешних сосредоточенных усилий соответствующие внутренние усилия равны нулю. Знаки внутренних сил определяются по сформулированным выше правилам. Поэтому для этих точек расчетную схему вычерчивать не будем. Для рассчитываемой рамы это точки 1, 4, 5, 7, 9. Соответственно, для этих точек можно не использовать индексы Л, П, Н, В, так как сечения определяются однозначно.

Точка 1.

Точка 4. - растянуто нижнее волокно.

Точка 5.

Точка 7.

Точка 10.

Точка 2.

Сечение слева

- растянуто верхнее волокно

Сечение справа.

- растянуто нижнее волокно.

Сечение ниже

- растянуто правое волокно.

Точка 3.

Так как в точке 3, соединяются два участка прямого стержня и здесь нет сосредоточенных внешних усилий, значения внутренних усилий в сечениях слева и справа одинаковы.

- растянуто нижнее волокно.

Точка 6.

Сечение выше.

- растянуто правое волокно.

Сечение слева.

- растянуто нижнее волокно.

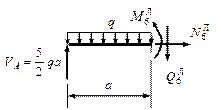
Сечение справа.

- растянуто нижнее волокно.

Точка 8.

Сечение выше.

- растянуто волокно справа.

Сечение справа.

- растянуто волокно справа.

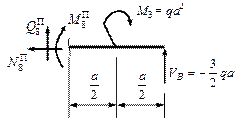
Точка 9.

Сечение слева.

- растянуто волокно справа.

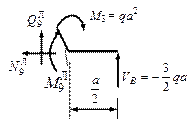
Сечение справа.

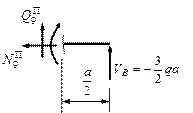
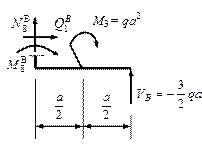
3. Строим эпюры внутренних усилий – N, Q, M.

Предварительно выпишем полученные значения внутренних усилий по участкам (табл.10.1). В первой графе таблице идут номера точек ограничивающих участок. Значения нормальных сил приведены на весь участок. Для поперечных сил и изгибающих моментов приведены их значения вначале и в конце участка – начало участка соответствует первой точке номера участка, конец – второй. Например для участка 2 – 6, начало участка в точке 2, конец участка в точке 6. Для моментов, указывается с кокой стороны стержня откладывается указанное значение (растянутое волокно): н – снизу, в – сверху, л – слева, п – справа. При нулевом значении момента указывается растянутое волокно в окрестности точки.

Таблица 10.1

Участок	N	Qнач	Qкон	Mнач	Раст.	Mкон	Раст.
1 - 2	0	-qa	-qa	0	в	qa^2	в
2 - 3	-4qa	qa	0	0,5qa^2	н	qa^2	н
3 - 4	-4qa	0	0	qa^2	н	qa^2	н
2 - 6	-2qa	-4qa	-2qa	1,5qa^2	л	4,5qa^2	л
5 - 6	0	- 2,5qa	-1,5qa	0	н	2qa^2	н
6 - 7	2qa	-2qa	-2qa	2qa^2	н	0	н
6 - 8	qa	0	0	2,5qa^2	п	2,5qa^2	п
8 - 9	0	1,5qa	1,5qa	2,5qa^2	в	1,75qa^2	в
9 - 10	0	1,5qa	1,5qa	0,75qa^2	в	0	в

Для построения эпюры изгибающих моментов на участках с распределенной нагрузкой (участки 2 – 3, 2 – 6 и 5 – 6) эпюры строятся по трем точкам (рис.10.32).

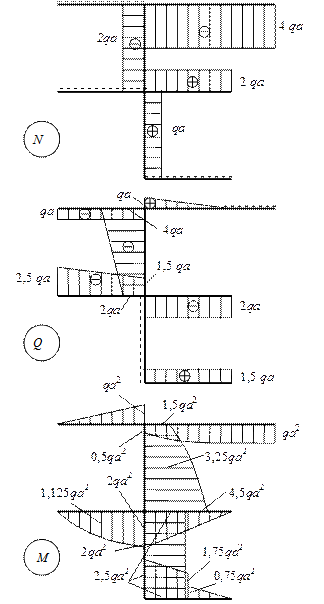
Рис. 10.32

Так как в рассматриваемой раме на участках с распределенной нагрузкой нет нулевых значений поперечной силы (нет экстремальных значений изгибающих моментов), то вычислим моменты в серединах участков:

участок 2 – 3

участок 2 – 6

участок 5 – 6

Эпюры внутренних усилий в раме, построенные на основании приведенных сечениях, приведены на рис. 10.32.

4. Проводим контроль характерных особенностей полученных эпюр.

а) Эпюры нормальных усилий N постоянны на всех участках.

б) Эпюры поперечных сил Q постоянны на участках 1-2, 3-4, 5-6, 6-8, 8-9, 9-10, где отсутствует распределенная нагрузка. На участках 2-3, 2-6, 5-6, где действует равномерно распределенная нагрузка, эпюры изменяются линейно.

в) На участках 1-2, 5-6, 8-9, 9-10, где поперечные силы постоянны, изгибающие моменты изменяются линейно. На участках 3-4, 6-8, где поперечные силы равны нулю, изгибающие моменты постоянны. На участках 2-3, 2-6, 5-6, где действует распределенная нагрузка, эпюры изгибающих моментов криволинейны – квадратная парабола, выгнутая в сторону действия нагрузки, и согласуются с эпюрами поперечных сил на этих участках в соответствии с соотношениями Журавского. Так как на участках с распределенной нагрузкой эпюра поперечных сил не пересекает оси стержней (нет точек, где Q = 0), то на этих участках нет экстремумов изгибающих моментов.

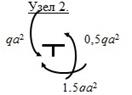
5. Проводим проверку равновесия узлов.

а) Проверка равновесия узлов на совместное действие нормальных и поперечных сил.

Узел 8 также находится в равновесии, так как на него действуют два равных, противоположно направленных изгибающих момента

Таким образом, все узлы рамы находятся в равновесии.

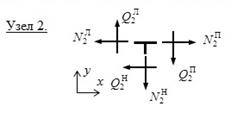
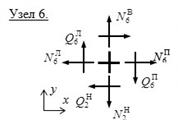
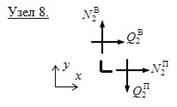
б) Проверка равновесия узлов по изгибающим моментам

Пример 10.

Построить эпюры M_x , Q_y , N_z для заданной плоской рамы (рис.10.33).

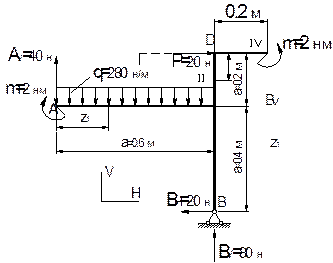
Рис.10.33

Решение.

1. Направим вертикальные реакции вверх. Горизонтальная составляющая должна быть равна силе P, но противоположна ей по направлению, что следует из уравнения равновесия Для определения реакций составим уравнения равновесия:

Положительные значения реакций указывают на совпадение первоначально выбранных направлений усилий с истинным. Для проверки их численных значений рассмотрим уравнение равновесия , которое должно удовлетворяться тождественно при найденных значениях реакций:

Таким образом, реакции найдены правильно.

2.Число участков в данном случае равно числу стержней рамы.

а)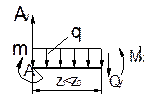 б) в)

Рис.10.34

Применяя метод сечений к I участку (рис.10.34, а), получим выражения для внутренних силовых факторов:

Видно, что эпюра Q_y линейна, а эпюра M_x является параболой. При (опора А) будут В сечении, где Q_y обращается в нуль, момент M_x достигает максимума:

В сечении =0,6 м значения силовых факторов будут: На первом участке полученные значения M_x , Q_y , N_z наносим на соответствующие эпюры (рис. 10.35).

Применяя метод сечений на втором участке (рис.10.34, б) получим формулы для силовых факторов:

Вычислим значения в сечениях и по ним построим соответствующие эпюры на втором участке. Применение метода сечений на третьем и четвертом участках (рис.10.34, в). Применяя метод сечений дает следующие выражения для внутренних силовых факторов:

Видно, что эпюра M_x на третьем участке линейна, а на четвертом участке постоянна. Найдя соответствующие значения M_x и Q_y , в крайних сечениях третьего и четвертого участков, завершаем построение эпюр M_x и Q_y и эпюру N_z для заданной плоской рамы (рис. 10.35).

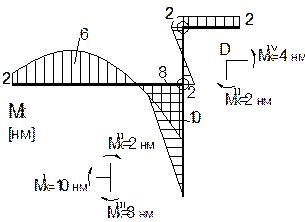
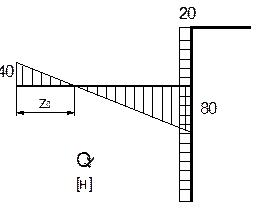
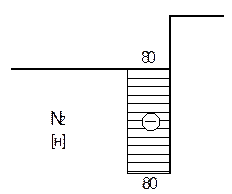
Рис.10.35

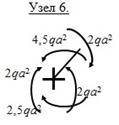
Для плоской рамы необходима также проверка равновесия узлов. Рассмотрим равновесие узла С, в котором соединены три стержня. Вырежем участок рамы вблизи этого узла (рис.10.35) и приложим соответствующие моменты M_x для трех участков по направлению сжатых волокон. Нетрудно видеть, что узел С находиться в равновесии, так как имеем Аналогично проверяем узел D (рис.10.35). В узле, где соединяются два стержня и не приложены внешний сосредоточенный момент, найденное значение для одного стрежня можно перенести раствором циркуля на другой стержень.

Пример 11.

Для статически определимой системы плоской рамы в виде ломаного бруса (рис. 10.36, а) построить эпюры M_x и Q_y и эпюру N_z ;

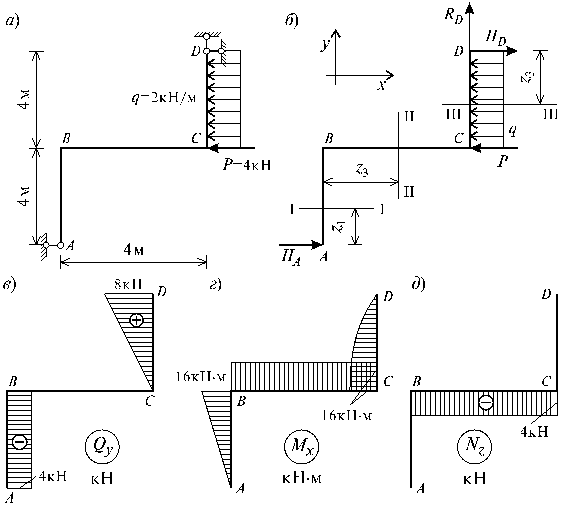
Рис.10.36

Решение.

Заданная плоская стержневая система (рис. 10.36, а), элементы которой представляют собой прямолинейные стержни, жестко соединенных между собой, называется рамой. При произвольном характере нагружения, в поперечных сечениях элементов заданной системы возникают следующие три силовых фактора: поперечная сила Q, изгибающий момент M и продольная сила N. Главной отличительной особенностью рамной системы от других стержневых систем является то, что в деформированной состоянии угол сопряжения между различными элементами равен углам сопряжения элементов до нагружения системы.

Правило знаков для Q_y , M_x и N_z и порядок построения их эпюр для таких систем остаются прежними.

Так как заданная система имеет только три внешние связи (вертикальную и горизонтальную в т. D и горизонтальную в т. А), следовательно, при общем характере нагружения возникает всего три опорные реакции. Как нам уже известно, для плоских систем можно воспользоваться только тремя уравнениями равновесия статики для определения опорных реакций, поэтому заданная система является статически определимой.

1) Определение опорных реакций.

Составив уравнения равновесия для всей рамы и решив их, получим:

R_D = 0;

-H_A 8 + Р 4 + q 4 2 = 0,    

H_D 8 - Р 4 - q 4 6 = 0,    

Проверка: H_A + H_D - Р - q 4 = 0;

4 + 8 - 4 - 2 4 = 0;    

12 - 12 = 0;    

0 = 0.

Уравнение равновесия превращается в тождество, что говорит о правильности вычисления опорных реакций.

2) Определение количества участков

Так как, в рамах границами участков являются точки приложения сил и точки изменения направления оси элементов системы, то заданная система имеет три участка: участок I - АВ, участок II -ВС, участок III - СD (рис. 10.36, б).

3) Составление аналитических выражений Q_y, M_x и N_z и определение их значений в характерных сечениях каждого участка

Определение внутренних силовых факторов в сечениях рам производится также с помощью метода сечений. Однако при выполнении разрезов всегда следует выяснить, какую из частей рамы считать левой, а какую правой. Для этого предполагают, что обход рамы ведется слева направо, т.е. от А к В, от В к С, от С к D. При этом наблюдение ведут с нижней стороны участков, находясь лицом к оси участков.

Участок I () (рис. 10.37).

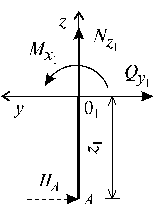
Рис.10.37

Проведя сечение в пределах этого участка, рассмотрим равновесие левой отсеченной части длиной z₁ . Составив уравнение равновесия и и для этой части и решив их относительно и , получим аналитические выражения изменения Q_y , M_x и N_z на участке I:

- уравнение прямой;

- нормальная сила отсутствует.

Величины Q_y , M_x и N_z в граничных сечениях участка будут равны:

при z₁ = 0

при z₁ = 4 м

Участок II () (рис. 10.38).

Сделав сечение в пределах этого участка, составим уравнения равновесия для левой части:

Рис.10.38

Знак “минус” перед говорит о том, что элемент ВС сжат, а не растянут. Из полученных уравнений видно, что на участке II поперечная сила равна нулю, а изгибающий момент и нормальная сила постоянны.

Участок III () (рис. 10.39). Приняв начало координат в сечении D и сделав разрез в пределах этого участка, рассмотрим равновесие правой отсеченной части длиной z₃ .

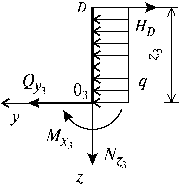
Рис.10.39

Составив уравнения равновесия и и решив их, получим:

- уравнение прямой.

- уравнение квадратной параболы;

Ординаты эпюр найдем из полученных выражений, подставив в них значения z₃, соответствующие граничным сечениям участка:

при z₃ = 0

при z₃ = 4 м    

Для уточнения очертания квадратной параболы определим величину при z₃ = 2 м:

4) Построение эпюр Q_y , M_x и N_z для рамы

Отложив в масштабе перпендикулярно к оси каждого элемента рамы полученные значения Q_y , M_x , N_z в граничных и промежуточных сечениях участка и соединяя концы ординат линиями, соответствующими выражениям Q_y , M_x и N_z , строим их эпюры (рис. 10.36, в, г, д).

Правильность построения эпюр внутренних усилий подтверждается на основе статической проверки, заключающейся в том, что условия равновесия рамы (), как в целом, так и любой ее отсеченной части, под воздействием внешних нагрузок и усилий, возникающих в проведенных сечениях, соблюдаются тождественно.

Пример 12.

Построить эпюры Q, M и N и подобрать двутавровое поперечное сечение для рамы (рис. 10.40, а), если известно: Р=20 кН, m=10 кНм, l=2 м, h=3 м, =160 МПа.

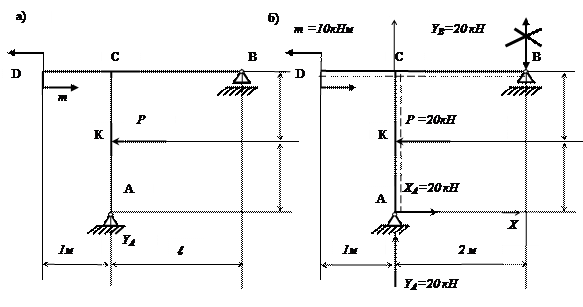
Рис.10.40

Решение.

1. Определение опорных реакций (рис. 10.40,б)

Проверка:

2. Построение эпюр Q, М и N

Разбиваем раму на участки, выбираем пунктирное волокно (рис. 10.40,б).

Участок АК:

Участок КС:

Участок DС:

Участок ВС:

Эпюры показаны на рисунке 10.41, а, б, в.

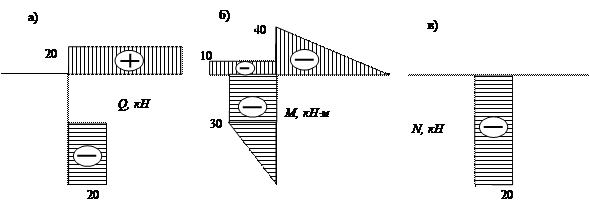
Рис.10.41

3. Проверка правильности построения эпюр Q, М и N

Проверка производится методом вырезания узлов. Узел должен находиться в равновесии, т. е. должно выполняться условие равенства нулю суммы проекций всех внешних и внутренних сил на оси X, Y, а также равенства нулю суммы всех внешних и внутренних моментов относительно узла.

Для проверки вырезаем узел С (рис. 10.42) и прикладываем к нему внешние силы беря их с заданной схемы (на рис. 1 внешних сил к узлу С не приложено), а также поперечные силы, изгибающие моменты и продольные силы, беря их направление и величину с эпюр Q, M и N (рис. 10.41, а, б, в).

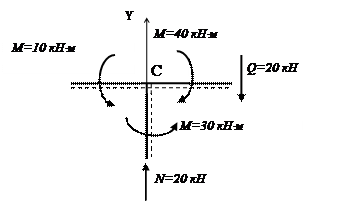
Рис.10.42

Из рисунке 10.42 видно, что

4. Подбор сечения

Производим подбор сечения рамы по условию прочности при =160 Мпа.

- берется с эпюры изгибающих моментов (рис.10.41,б)

По ГОСТ 8239-89 подбираем двутавр № 22^а, W_x=251 см³.

Рамы на двух опорах с промежуточным шарниром

Как отмечалось выше, рамы на двух шарнирно-неподвижных опорах с одним промежуточным шарниром также являются статически определимыми.

Пример 13.

Рассмотрим построение эпюр для рамы с промежуточным шарниром (рис.10.43,а)

Решение.

В дополнение к условиям равновесия, здесь для определения неизвестных реакций () используются еще два условия: и , каждое из которых по своей сути выражает факт равенства нулю изгибающего момента в промежуточном шарнире С (рис.10.43,а).

Для определения четырех неизвестных реакций возможно использование различных комбинаций уравнений равновесия, но чаще всего используются следующие уравнения:

При этом для проверки вычисленных реакций служат уравнения:

При заданных нагрузках (рис.10.43,а) уравнения равновесия принимают вид:

Знак "-", полученный при вычислении реакции , говорит о необходимости изменить принятое для нее направление на противоположное (перечеркнутая стрелка на рис.10.43,а).

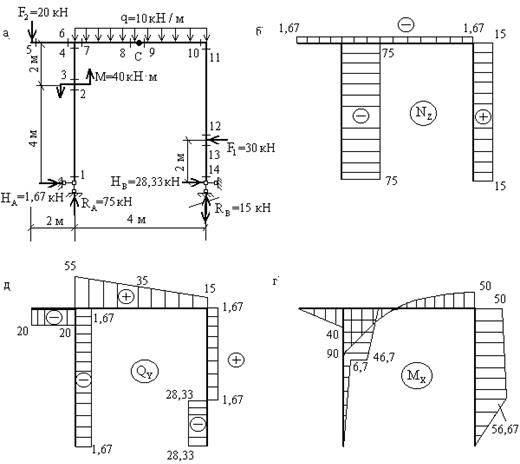
Рис.10.43

Проверяем правильность вычисления опорных реакций.

Теперь вычисляем значения в характерных сечениях, выбирая для сечений 1-8 левую отсеченную часть, а для сечений 9-14 - правую.

Из рассмотрения левой отсеченной части:

(сжаты правые волокна стойки);

(сжаты нижние волокна ригеля);

Вновь подчеркнем, что знаки "+" и "-" для изгибающих моментов принимаются относительно, то есть для разграничения противоположно направленных моментов, а эпюра строится со стороны сжатых волокон.

Из рассмотрения правой отсеченной части:

(сжаты верхние волокна ригеля)

(сжаты правые волокна стойки)

Эпюры , построенные по вычисленным значениям, приведены на рис.10.43,б,в,г.

Пример 14.

Рассмотрим двухдисковую конструкцию, состоящую из двух рам (трехшарнирная рама) (рис.10.44).

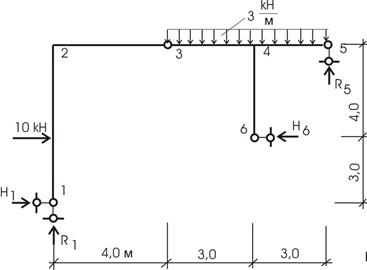
Рис.10.44

Решение.

Определение опорных реакций для данной конструкции возможно только двумя первыми приемами.

1. Использование свойств шарнира.

Видим, что ни одно из уравнений не дает решения.

Решаем систему из 4 уравнений с 4 неизвестными:

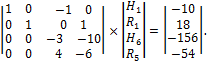
Решение системы уравнений дает

кH; кH;

кH; кH.

Знак минус, как мы уже отмечали, указывает, что направление реакции Н₁ нами выбрано ошибочно и для построения внутренних усилий (эпюры М, Q, N) ее направление нужно поменять на обратное.

2. Расчленение конструкции (рис. 10.45,а, б).

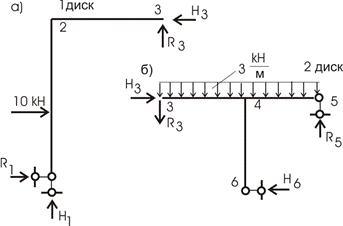
Рис.10.45

Составляем уравнения статики для каждого диска.

1 диск:

2 диск:

Получили 6 неизвестных и 6 уравнений:

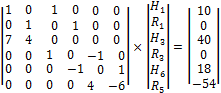
Решение системы уравнений дает:

кH; кH;

кH; кH;

кH; кH.

Сравнивая полученные результаты двумя приемами, видим, что они практически одинаковы.

Построение эпюр внутренних усилий проведем для каждого элемента.

1 диск (рис. 10.46).

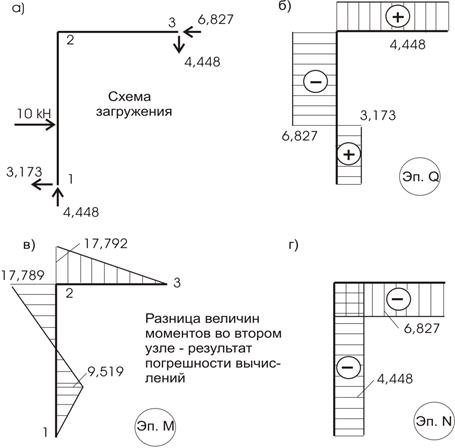
Рис.10.46

Разница моментов во втором узле – результат погрешности вычислений.

2 диск (рис. 10.47).

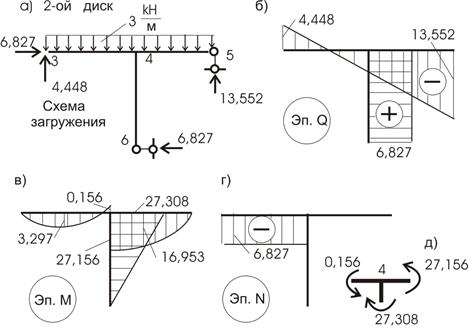
Рис.10.47

Проверка равновесия узла 4 дает (рис. 10.47,д):

27,308-27,156-0,156=0;

27,308-27,312=0;

Можем считать, что узел в равновесии (погрешность составляет 0,014%).

Графики изменения внутренних усилий для конструкции в целом показаны на рисунках 10.48,а, б, в.

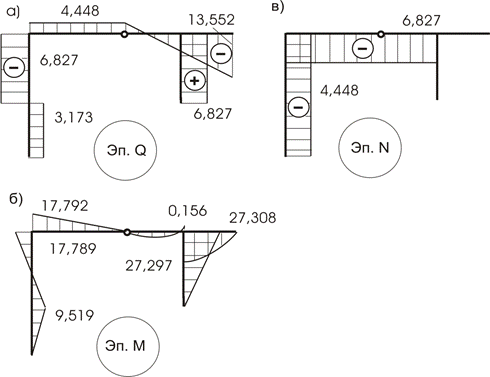
Рис.10.48

Пример 15.

Рассмотрим многодисковую раму (рис.10.49).

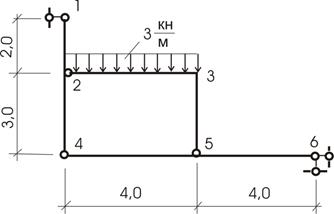
Рис.10.49

Решение.

Кинематический анализ дает:

Конструкция неизменяемая и неподвижная. Определение опорных реакций в связях (шарнирах) проведем расчленением конструкции на ее составляющие элементы (другие приемы здесь неприемлемы).

1 диск (элемент) – рис. 10.50,а.

Составляем для 1 элемента уравнения статики:

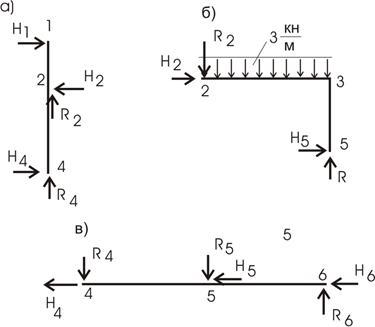
Рис.10.50

2 диск (элемент) – рис. 10.50,б.

3 диск (элемент) – рис. 10.50,в.

Систему уравнений представим в матричной форме:

.

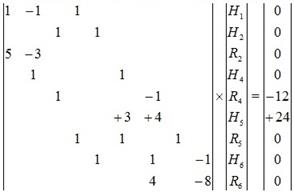Решение системы дает:

кH; кH; кH;

кH; кH; кH;

кH; кH; кH.

Эпюры внутренних усилий строим по элементам (рис. 10.51, 10.52, 10.53), а потом объединяем в одно целое (рис. 10.54). Нужно помнить, что в схемах загружения усилия в связях прикладываем с учетом их знака: если получили знак минус, то направление усилия меняем на противоположное.

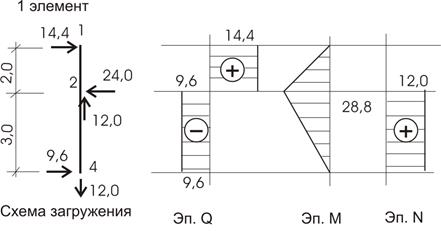
Рис.10.51

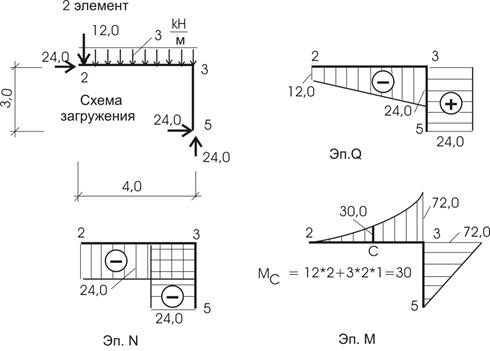
Рис.10.52

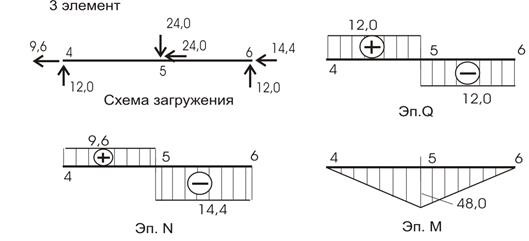
Рис.10.53

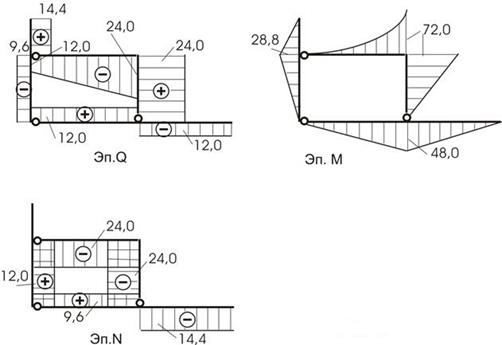
Рис.10.54

Расчет комбинированных конструкций

Комбинированные конструкции – конструкции, состоящие из сочетания рам, балок, ферм.

Пример 16.

Для примера рассмотрим конструкцию, показанную на рис.10.55 (конструкция мостового перехода).

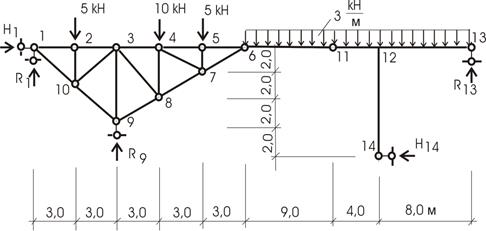
Рис.10.55

Решение.

1. Кинематический анализ.

Для конструкции в целом

Расчленим конструкцию на ее элементы:

1-ый элемент – ферма

Ферма - геометрически неизменяемая конструкция (диск), опирающаяся на 3 опорных стержня, следовательно, является основной конструкцией. Балка и рама (второй и третий элементы) крепятся к ферме с помощью связей – шарнирами 6 и 11.

2. Опорные реакции (усилия) в связях

Расчленим конструкцию на три элемента: ферму, балку, раму.

1- ый элемент (рис. 10.56)

2 ой элемент (рис. 10.57,а)

или

Отсюда находим кН;

из 2 уравнения

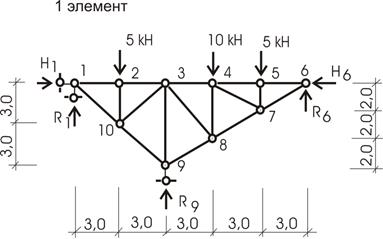
Рис.10.56

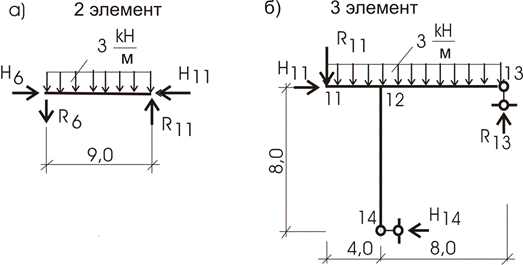
Рис.10.57

3-ий элемент (рис.10.57,б)

или

Усилия в связях 2 и 3 элементов определены, что позволит определить и усилия в связях 1 элемента:

Из третьего уравнения:

из второго:

Знание усилий в связях позволяет одним из разобранных путей построить эпюры внутренних усилий в балке и раме (рис. 10.58) и определить усилия в стержнях фермы (таблица 10.2).

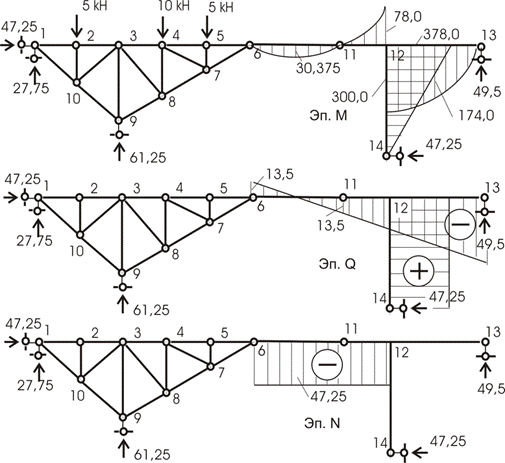
Рис.10.58

Таблица 10.2

Стержень	1-2	2-3	3-4	4-5	5-6	6-7	7-8	8-9
Величина усилия	-19,5	-19,5	-23,25	-26,98	-26,98	-24,32	-28,82	-36,31

Стержень	9-10	1-10	2-10	3-10	3-9	3-8	4-8	4-7	5-7
Величина усилия	-42,78	-39,25	-5	3,53	-10,85	10,44	-12,5	4,50	-5

Вопросы для самопроверки

- Дайте определение фермы.

- Какую нормальную силу называют положительной? Отрицательной?

- Запишите условие равновесия узла фермы.

- Какую раму называют плоской?

- Какие внутренние силовые факторы могут возникнуть в поперечных сечениях плоской рамы?

- Какие условия равновесия необходимо записать для определения опорных реакций плоской рамы?

- Какие закономерности для изгибающего момента следуют из условий равновесия узлов рамы?

- Сформулируйте правило знаков для нормальной силы.

- Сформулируйте правило знаков для поперечной силы.

- Сформулируйте правило знаков для изгибающего момента.

- Признаки равновесия узла рамы?

- Уравнение статики для одномерных задач, плоских (двухмерных) и трехмерных.

- Как определяются опорные реакции в статически определимых рамах?

- Определение изгибающего момента на примере расчета рамы. Правило знаков для изгибающих моментов.

- Определение перерезывающей силы на примере расчета рамы. Правило знаков для перерезывающей силы.

- Определение продольной силы N на примере расчета рамы. Правило знаков для продольной силы.

- Проверка правильности построения эпюр M, N, Q.

- Система уравнений равновесия для расчета статически определимых стержневых систем. Ее особенности в случае геометрической изменяемости системы.

- Внутренние усилия в стержнях рам и балок. Правила построения и свойства эпюр изгибающего момента, перерезывающего и продольного усилий.

- Как определяют опорные реакции в простых, однопролетных балках?

- Что такое продольное усилие в сечении?

- Что такое перерезывающая сила в сечении?

- Что собой представляет изгибающий момент в сечении?

- На каких волокнах откладывается величина изгибающего момента?

- Величина изгибающего момента по длине стержня (участка стержня) меняется по линейному закону, в каком случае?

- На эпюре изгибающих моментов наблюдается точка излома, в каком случае?

- На эпюре изгибающих моментов наблюдается скачок, в каком случае?

- Чем определяется положительное направление внутренних усилий?

- Что такое простое сечение в плоской расчетной схеме?

- Какое правило знаков принято при построении эпюр М и Q?

- Какой вид имеют эпюры изгибающих моментов и поперечных сил на участках, где отсутствует нагрузка?

- Определение внутренних усилий в статически определимых рамах. Построение эпюр M, Q, N в статически определимых рамах.

- Как изменяются изгибающий момент и поперечная сила на участке, где действует равномерно распределенная нагрузка q, или сосредоточенная сила F, или сосредоточенный момент m?

- Чему равен момент в шарнире (или на шарнирной опоре) если бесконечно близко от него не приложен внешний сосредоточенный момент?

- Как “подвешивается” балочная эпюра изгибающих моментов простой балки на участке балки длиной l, загруженной равномерно распределенной нагрузкой q (или сосредоточенной силой F, или сосредоточенным моментом M), если известны изгибающие моменты по концам этого участка?

- Определение внутренних усилий в стержнях сложных статически определимых рам. Способы контроля правильности построенных эпюр внутренних усилий.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00