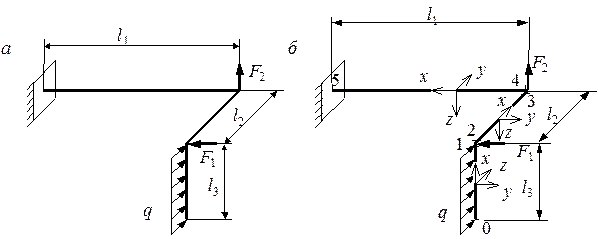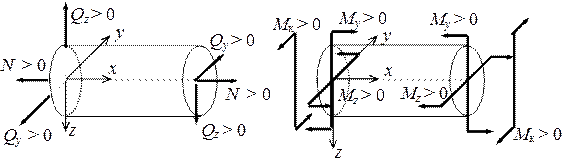Главная
Лекция 11. Пространственные
системы
Содержание
Внутренние усилия пространственных систем
Опоры пространственных систем и их реакции
Кинематический анализ пространственных
систем
Определение перемещений пространственных
систем
Построение эпюр в плоско-пространственных
системах (ППС)
Построение эпюр в ломаных стержнях
Расчет на прочность и подбор сечения ломаных пространственных стержней
Задачи для самостоятельного решения
Внутренние усилия пространственных систем
Все сооружения являются пространственными, и на них действуют нагрузки, лежащие в разных плоскостях. Поэтому и расчетные схемы сооружений должны быть пространственными.
Как мы
знаем, в плоских стержневых системах определяются три внутренних усилия M, Q, N (рис. 1,а).
А в пространственных стержневых системах таких усилий шесть: изгибающие моменты
My и Mz, крутящий момент Mx, поперечные силы Qy
и Qz, продольная сила N (рис.1,б).
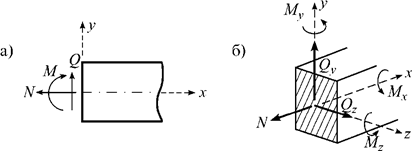
Рис. 1
Опоры пространственных систем и их реакции
Пространственные системы опираются на пространственные опоры, которые имеют свои кинематические и статические свойства. Обычно связи опор считаются жесткими, а перемещения по их направлениям равны нулю. При определении опорных реакций используются известные в механике уравнения равновесия.
В отличие от плоских систем опоры пространственных систем могут быть 15 типов. Из них рассмотрим четыре типа опор.
1. Шаровая подвижная опора (рис. 2,а). На рисунке изображается как шарик, свободно качающийся между опорной плоскостью и элементом конструкции, а в расчетной схеме – как одна вертикальная связь. У этой опоры имеется пять степеней свободы – она дает возможность поступательных перемещений в двух и поворотов в трех направлениях. В ней возникает только одна опорная реакция Ry.
2. Шаровая опора на цилиндрических катках (рис. 2,б). На рисунке изображается как шарик между двумя балансирами, один из которых жестко связан с элементом конструкции, а другой находится на цилиндрических катках. В расчетной схеме изображается в виде двух связей. У этой опоры имеется четыре степени свободы – одно поступательное перемещение и три поворота. В ней возникают две реакции Ry и Rz.
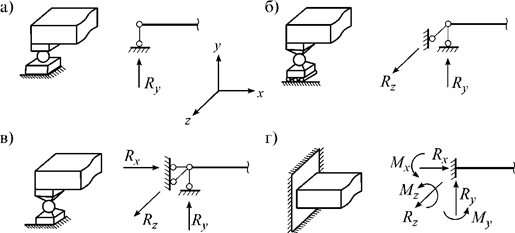
Рис. 2
3. Шаровая неподвижная опора (рис. 2,в). На рисунке изображается как шарик между двумя балансирами, жестко связанными с элементом конструкции и основанием, а в расчетной схеме в виде трех связей. У этой опоры есть три степени свободы – возможность поворота в трех направлениях. В ней возникают три реакции Rx, Ry и Rz.
4. Заделка (рис. 2,г). На рисунке изображается как заделанный брус (или стержень), а в расчетной схеме как обычная заделка. У заделки степеней свободы нет. В ней возникают три реакции Rx, Ry и Rz и три реактивных момента Mx, My и Mz.
Кроме рассмотренных здесь, еще имеется 11 различных опор.
Реакции статически определимых пространственных систем определяются из шести уравнений равновесия. Имеется четыре варианта записи этих уравнений, из которых рассмотрим только два:
1. ΣX=0; ΣY=0; ΣZ=0; ΣMx =0; ΣMy =0; ΣMz =0.
Здесь ΣX, ΣY, ΣZ – суммы проекций на три оси x, y, z, которые не должны лежать в одной плоскости и быть параллельными; суммы моментов не обязательно составлять относительно тех же осей.
2. ΣM1=0; ΣM2=0; ΣM3=0; ΣM4=0; ΣM5=0; ΣM6=0.
Здесь 1, 2, …, 6 – шесть любых осей в пространстве. Но:
– эти оси не должны пересекать одну прямую;
– число параллельных осей не должно быть больше трех;
– если три оси пересекаются в одной точке, остальные три не должны быть параллельными.
Кинематический анализ пространственных систем
Как известно, расчетная схема сооружения должна быть геометрически неизменяемой. Многие условия и выводы, полученные при кинематическом анализе плоских систем, применимы и при анализе пространственных систем. Но их недостаточно. Потому вводятся новые понятия и рассматриваются новые способы анализа их геометрической неизменяемости.
Любую геометрически неизменяемую часть пространственной системы будем называть телом. Любое тело без связей имеет шесть степеней свободы – три независимых поступательных перемещения и три поворота. Следовательно, для исключения этих степеней свободы тело нужно закреплять как минимум шестью связями.
Простейший способ закрепления тела к земле показан на рис. 3,а, где имеется три типа опор – шаровая подвижная опора A, шаровая опора на цилиндрических катках B и шаровая неподвижная опора C. Из них опора C исключает три поступательных перемещения тела, опора B – два поступательных перемещения и опора A – одно поступательное перемещение. Таким образом получается геометрически неизменяемая система.
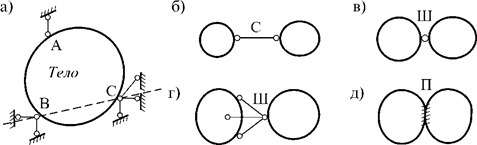
Рис. 3
Связи, соединяющие два тела, могут быть разными. Простейшая связь в виде стержня (С) показана на рис. 3,б. Если же два тела соединяются шаровым шарниром (рис.3,в), то это соединение эквивалентно трем связям (рис. 3,г). Припайка, жестко связывающая два тела (рис.3,д), эквивалентна шести связям.
Если в пространственной системе имеется nТ тел, nШ шаровых шарниров, nC стержней, nc0 опорных связей и nП припаек, то число степеней свободы такой системы определяется по формуле
W = 6nТ – 3nШ – nC
– nc0 – 6nП .
Как и для плоской системы, для геометрической
неизменяемости пространственной системы необходимо выполнение условия W![]() 0.
0.
Определение перемещений пространственных систем
В пространственных стержневых системах в общем случае могут возникать шесть внутренних усилий. Поэтому формула вычисления перемещений по методу Мора содержит шесть компонент:
![]()
где индексом P обозначены усилия грузового состояния: ![]() – два изгибающих и крутящий моменты,
– два изгибающих и крутящий моменты, ![]() – две поперечные и продольная силы;
надчеркиванием обозначены соответствующие усилия единичного состояния;
– две поперечные и продольная силы;
надчеркиванием обозначены соответствующие усилия единичного состояния; ![]() – моменты инерции относительно осей y, z и полярный момент
инерции;
– моменты инерции относительно осей y, z и полярный момент
инерции; ![]() – коэффициенты формы сечения.
– коэффициенты формы сечения.
Определение перемещений по этой формуле проводится как и при определении перемещений плоских стержневых систем. В пространственных рамах влиянием продольных и поперечных сил обычно пренебрегают и учитывают только первые три члена этой формулы, а в фермах учитывается только последний член.
Построение эпюр в
плоско-пространственных системах (ППС)
Систему, состоящую из прямолинейных стержней, жестко соединенных между собой, расположенных в одной плоскости и нагруженных перпендикулярно к этой плоскости, будем называть плоско-пространственной.
В настоящей лекции будем рассматривать только жесткозащемленые плоско-пространственные системы (далее сокращенно ППС). При этом возможны два основных варианта:
1) система располагается горизонтально, нагрузки приложены в вертикальных плоскостях (рис.3.1,а,б),
2) система располагается в вертикальной плоскости, нагрузки приложены горизонтально (рис.3.1,в,г)
В первом случае (рис.3.1,а,б) в поперечных сечениях стержней
системы могут возникать поперечная сила ![]() , изгибающий момент
, изгибающий момент ![]() и
крутящий момент
и
крутящий момент ![]() ; во втором случае -
; во втором случае - ![]() . Очевидно, что поворотом на 90 градусов
системы второго вида (рис.3.1,в,г)
приводятся к системам первого вида, при этом
. Очевидно, что поворотом на 90 градусов
системы второго вида (рис.3.1,в,г)
приводятся к системам первого вида, при этом ![]() переходит в
переходит в ![]() - в
- в ![]() , поэтому в дальнейшем ограничимся
рассмотрением систем первого вида.
, поэтому в дальнейшем ограничимся
рассмотрением систем первого вида.
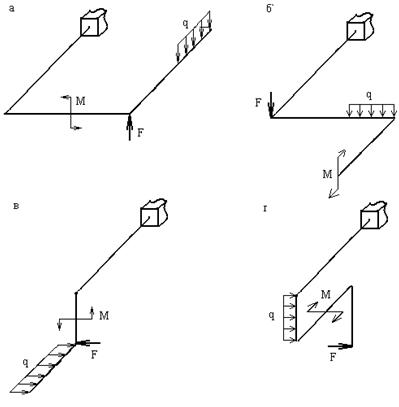
Рис.3.1
Известно, что при одновременном наличии в
сечениях изгибаемой стержневой системы внутренних моментов и внутренних сил
влияние последних на напряженно-деформированное состояние системы незначительно
(исключение составляет "короткие" стержни), поэтому исключим из
рассмотрения поперечную силу ![]() .
.
Итак, остановимся на правилах построения эпюр
![]() для
плоско-пространственных систем.
для
плоско-пространственных систем.
Прежде чем перейти к рассмотрению примеров на
построение эпюр внутренних силовых факторов вспомним, как определяются моменты относительно
тех или иных осей от сил, расположенных в пространстве.
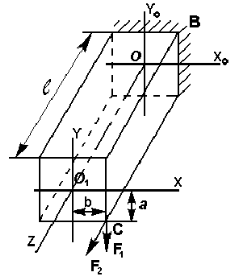
Рис.3.2
На рис.3.2 представлен брус и две силы F1 и F2, приложенные в точке С, расположенной в торцевой
плоскости бруса соответственно на расстоянии a и b в от осей X и Y.
Сила F1 параллельна оси Y, а сила F2 – оси Z.
Определить величину моментов относительно X0, Y0 и Z от этих
сил в сечении В бруса. Вычислим момент от силы F1 относительно Х0.
Плечо этой силы определяется расстоянием между плоскостью Х0ОУ0
в сечение B и параллельной ей вертикальной плоскостью, содержащей силу F1.
Это расстояние равно l.
Следовательно, в сечении В
(изгибающий момент в вертикальной плоскости) ![]() . Момент силы F1 относительно оси Y0 равен нулю так как сила
параллельна этой оси. Плечо силы F1
относительно оси Z определяется
расстоянием между плоскостью Y0OZ и параллельной ей вертикальной
плоскостью, содержащей силу F1(l). Тогда
крутящий момент
. Момент силы F1 относительно оси Y0 равен нулю так как сила
параллельна этой оси. Плечо силы F1
относительно оси Z определяется
расстоянием между плоскостью Y0OZ и параллельной ей вертикальной
плоскостью, содержащей силу F1(l). Тогда
крутящий момент ![]() . Если
смотреть на брус со стороны внешней нормали к поперечному сечению, то этот
момент направлен по часовой стрелке. Такое направление момента будем считать
отрицательным. Правило знаков для крутящих моментов, вообще говоря, условно и
может быть любым. Необходимо только моменты, скручивающие брус в разные
стороны, откладывать по разные стороны от нулевой линии эпюры.
. Если
смотреть на брус со стороны внешней нормали к поперечному сечению, то этот
момент направлен по часовой стрелке. Такое направление момента будем считать
отрицательным. Правило знаков для крутящих моментов, вообще говоря, условно и
может быть любым. Необходимо только моменты, скручивающие брус в разные
стороны, откладывать по разные стороны от нулевой линии эпюры.
Рассмотрим силу F2.
Момент от силы F2
относительно оси Z равен нулю, т.к.
сила F2 параллельна этой
оси. Плечо силы F2 относительно
оси Х0 и сечении В, определяемое
расстоянием между горизонтальной плоскостью X0OZ и параллельной ей горизонтальной
плоскостью, содержащей силу F2,
равен a,
следовательно изгибающий момент в вертикальной плоскости ![]() . Плечо силы F2 относительно оси Y0 в сечении В равно расстоянию между вертикальной
плоскостью Y0OZ и параллельной ей вертикальной
плоскостью, содержащей силу F2.
Это расстояние равно b.
Следовательно, изгибающий момент в горизонтальной плоскости
. Плечо силы F2 относительно оси Y0 в сечении В равно расстоянию между вертикальной
плоскостью Y0OZ и параллельной ей вертикальной
плоскостью, содержащей силу F2.
Это расстояние равно b.
Следовательно, изгибающий момент в горизонтальной плоскости ![]() . Эпюры
изгибающих моментов строятся на сжатом волокне. Итак, в сечении В будут возникать
следующие моменты:
. Эпюры
изгибающих моментов строятся на сжатом волокне. Итак, в сечении В будут возникать
следующие моменты:
изгибающий момент в
вертикальной плоскости ![]()
(в этом уравнении момент силы F2, сжимающие верхние волокна бруса, взят со знаком
плюс);
изгибающий момент в горизонтальной
плоскости ![]()
(сжаты волокна левой половины поперечного сечения
бруса);
крутящий момент ![]()
Закономерности изменения внутренних силовых факторов в
зависимости от характера действующих внешних нагрузок (сосредоточенная сила,
равномерно распределенная поперечная нагрузка, сосредоточенный момент)
устанавливаются так же, как для балок и плоских рам.
Пример
1.
Рассмотрим ППС (рис.3.3,а). Прежде чем строить для этой системы эпюры ![]() , построим эпюры
, построим эпюры ![]() для
каждой из четырех возможных нагрузок (они представлены на схеме), так как
вообще говоря, любые эпюры
для
каждой из четырех возможных нагрузок (они представлены на схеме), так как
вообще говоря, любые эпюры ![]() в силу
принципа независимости действия сил будут представлять собой алгебраическую
сумму этих простейших эпюр, построенных от каждой нагрузки в отдельности, но,
разумеется, с учетом места приложения нагрузок, их направлений и геометрической
конфигурации системы.
в силу
принципа независимости действия сил будут представлять собой алгебраическую
сумму этих простейших эпюр, построенных от каждой нагрузки в отдельности, но,
разумеется, с учетом места приложения нагрузок, их направлений и геометрической
конфигурации системы.
Для достижения максимальной общности будем
считать, что сила F, момент типа ![]() и
момент типа
и
момент типа ![]() (имеется в виду плоскость действия каждого из
них) приложены к концевому сечению (т.А
на рис.3.3,а), а распределенная
нагрузка приложена к первому от свободного конца участку стержня (стержень АВ
на рис.3.3,а). Причем, все построения будем выполнять в
общем виде, полагая, для наглядности, что a< l.
(имеется в виду плоскость действия каждого из
них) приложены к концевому сечению (т.А
на рис.3.3,а), а распределенная
нагрузка приложена к первому от свободного конца участку стержня (стержень АВ
на рис.3.3,а). Причем, все построения будем выполнять в
общем виде, полагая, для наглядности, что a< l.
Пусть к
плоско-пространственной системе (рис.3.3,в) приложена только сила F. Построим эпюры ![]() для
заданной системы. Здесь, как и при любой другой внешней нагрузке, более сложным
является построение эпюры изгибающих моментов
для
заданной системы. Здесь, как и при любой другой внешней нагрузке, более сложным
является построение эпюры изгибающих моментов ![]() . В соответствии с ранее оговоренными
принципами, для построения эпюры
. В соответствии с ранее оговоренными
принципами, для построения эпюры ![]() в заданной ППС выделим 6 характерных сечений. Так как
имеется жесткая заделка, то расчет ведем от свободного конца. При вычислении
изгибающего момента очень важно правильно определить плоскость изгиба стержня,
которому принадлежит рассматриваемое характерное сечение, т.к. плечо
действующей нагрузки необходимо определить именно в плоскости изгиба.
в заданной ППС выделим 6 характерных сечений. Так как
имеется жесткая заделка, то расчет ведем от свободного конца. При вычислении
изгибающего момента очень важно правильно определить плоскость изгиба стержня,
которому принадлежит рассматриваемое характерное сечение, т.к. плечо
действующей нагрузки необходимо определить именно в плоскости изгиба.
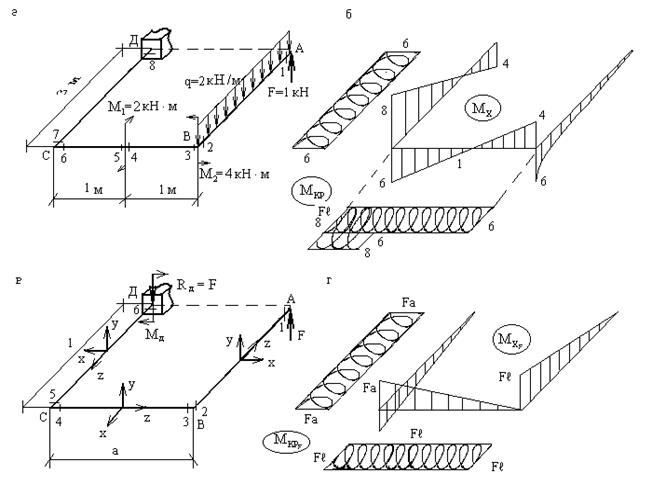
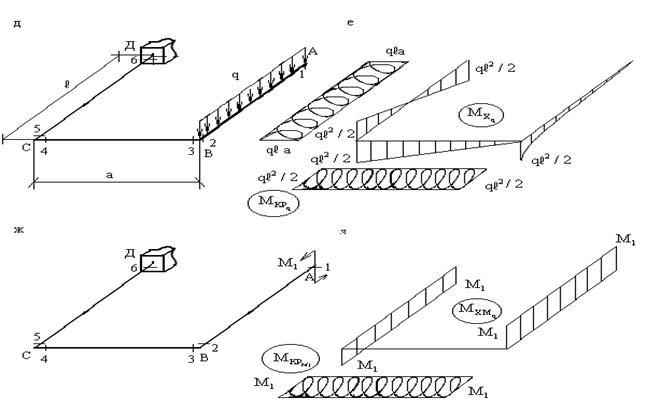
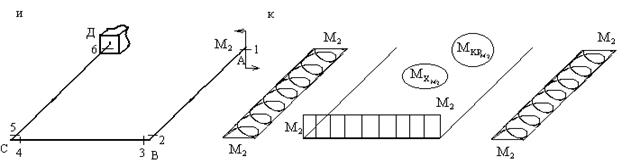
Рис.3.3
Стержень АВ изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа;
![]()
![]() (сжаты
верхние волокна).
(сжаты
верхние волокна).
Стержень ВС изгибается в вертикальной плоскости, параллельной плоскости чертежа:
![]() (сила F не имеет плеча в плоскости изгиба!);
(сила F не имеет плеча в плоскости изгиба!);
![]() (сжаты верхние волокна).
(сжаты верхние волокна).
Стержень СД, как и стержень АВ, изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа.
![]() (сжаты нижние волокна).
(сжаты нижние волокна).
![]() (сила F не имеет плеча в плоскости изгиба).
(сила F не имеет плеча в плоскости изгиба).
Остановимся подробнее на определении
изгибающего момента ![]() . Как видно из приведенных выше значений:
. Как видно из приведенных выше значений: ![]() , то есть моменты в сечениях 2 и 5 (обратим
внимание на их расположение, а не на нумерацию, которая, естественно, может
быть совершенно произвольной) одинаковы по величине, но противоположны по
направлению. Это утверждение можно доказать.
, то есть моменты в сечениях 2 и 5 (обратим
внимание на их расположение, а не на нумерацию, которая, естественно, может
быть совершенно произвольной) одинаковы по величине, но противоположны по
направлению. Это утверждение можно доказать.
Причем, возможно как строгое доказательство, так и некоторые "нестрогие" рассуждения, приводящие к тому же факту. Начнем с последних. Под действием приложенной силы F (рис.3.3,в) происходит "перекос" системы: точка В смещается вверх, а точка С - вниз; при этом обе точки располагаются на одинаковом расстоянии (в вертикальной плоскости, перпендикулярной плоскости чертежа) от линии действия силы F, следовательно, моменты в сечениях 2 и 5 одинаковы, но противоположны по знаку.
Для иллюстрации другого подхода к
"нестрогому" доказательству утверждения о том, что ![]() введем
в рассмотрение так называемую скользящую систему координат (рис.3.3,в). Такое
название связано с тем, что координатные оси как бы скользят вдоль ломаной
продольной оси системы, не поворачиваясь вокруг нее. При этом на каждом участке
плоско-пространственной системы ось z направлена вдоль продольной оси
соответствующего стержня, ось y - вверх (или вниз) при расположении системы в
горизонтальной плоскости, а ось x остается перпендикулярной к плоскости yoz. Как следует из чертежа, на участках АВ и СД ось x
имеет противоположное направление, следовательно, моменты
введем
в рассмотрение так называемую скользящую систему координат (рис.3.3,в). Такое
название связано с тем, что координатные оси как бы скользят вдоль ломаной
продольной оси системы, не поворачиваясь вокруг нее. При этом на каждом участке
плоско-пространственной системы ось z направлена вдоль продольной оси
соответствующего стержня, ось y - вверх (или вниз) при расположении системы в
горизонтальной плоскости, а ось x остается перпендикулярной к плоскости yoz. Как следует из чертежа, на участках АВ и СД ось x
имеет противоположное направление, следовательно, моменты ![]() имеют
на этих участках разные знаки, а так как сечения 2 и 5 равноудалены от линии
действия силы F, то очевидно равенство моментов в этих сечениях по абсолютной
величине.
имеют
на этих участках разные знаки, а так как сечения 2 и 5 равноудалены от линии
действия силы F, то очевидно равенство моментов в этих сечениях по абсолютной
величине.
И, наконец, рассмотрим более строгое
доказательство. Двигаясь от свободного конца при выборе отсеченной части, мы
получили: ![]() (сжаты
верхние волокна). Определим момент
(сжаты
верхние волокна). Определим момент ![]() в
сечении 5, двигаясь при выборе отсеченной части со стороны жесткой заделки. Для
определения момента таким способом необходимо знать реакции заделки. При
действии на систему силы F из всех возможных в общем случае нагружения реакций в жесткой
заделке возникают реакция
в
сечении 5, двигаясь при выборе отсеченной части со стороны жесткой заделки. Для
определения момента таким способом необходимо знать реакции заделки. При
действии на систему силы F из всех возможных в общем случае нагружения реакций в жесткой
заделке возникают реакция ![]() и
опорный момент
и
опорный момент ![]() , определяемые из условий равновесия:
, определяемые из условий равновесия:
![]()
![]()
Теперь, двигаясь со стороны жесткой заделки, для сечения 5 получим:
![]() (сжаты
нижние волокна), то есть
(сжаты
нижние волокна), то есть ![]() (момент
(момент ![]() не
влияет на величину
не
влияет на величину ![]() , так как его плоскость действия
перпендикулярна плоскости изгиба).
, так как его плоскость действия
перпендикулярна плоскости изгиба).
Очевидно, что подобные
рассуждения можно провести при любой внешней нагрузке, поэтому в дальнейшем при
построении эпюры ![]() всегда будем руководствоваться правилом:
изгибающий момент в сечении 5 равен изгибающему моменту в сечении 2
(опять-таки, имеется в виду положение сечений, а не их порядковые номера) и
противоположен ему по знаку, при условии, что на участке 2-5 не приложен
сосредоточенный момент, который для сечения 5 является изгибающим, то
есть момент типа
всегда будем руководствоваться правилом:
изгибающий момент в сечении 5 равен изгибающему моменту в сечении 2
(опять-таки, имеется в виду положение сечений, а не их порядковые номера) и
противоположен ему по знаку, при условии, что на участке 2-5 не приложен
сосредоточенный момент, который для сечения 5 является изгибающим, то
есть момент типа ![]() (рис.3.3,а). При наличии на участке 2-5 такого
момента равенство ординат по модулю в сечениях 2 и 5 "искажается" на
величину
(рис.3.3,а). При наличии на участке 2-5 такого
момента равенство ординат по модулю в сечениях 2 и 5 "искажается" на
величину ![]() в
соответствующую направлению
в
соответствующую направлению ![]() сторону.
сторону.
Теперь построим эпюру ![]() .
.
Участок АВ не подвержен кручению, так как сила F приложена к продольной оси стержня АВ. Участок ВС закручивается силой F с плечом l, следовательно:
![]()
Участок СД также закручивается силой F, но с плечом a, то есть:
![]()
Эпюры ![]() и
и ![]() представлены на рис.3.3,г.
представлены на рис.3.3,г.
Аналогичным образом строятся эпюры изгибающих
и крутящих моментов от распределенной нагрузки q (рис.3.3,д),
сосредоточенного момента типа ![]() (рис.3.3,ж)
и сосредоточенного момента типа
(рис.3.3,ж)
и сосредоточенного момента типа ![]() (рис.3.3,и).
(рис.3.3,и).
Не останавливаясь детально на построении этих
эпюр, отметим некоторые особенности. Эпюра ![]() на
участке под распределенной нагрузкой (и только на этом участке!)- квадратная
парабола, направленная выпуклостью навстречу нагрузке. На участке СД -
противоположном тому, где приложена нагрузка q -
эпюра
на
участке под распределенной нагрузкой (и только на этом участке!)- квадратная
парабола, направленная выпуклостью навстречу нагрузке. На участке СД -
противоположном тому, где приложена нагрузка q -
эпюра ![]() пересекает ось в точке, расположенной напротив
равнодействующей распределенной нагрузки (рис.3.3,д).
пересекает ось в точке, расположенной напротив
равнодействующей распределенной нагрузки (рис.3.3,д).
Анализ эпюр от сосредоточенных моментов ![]() (рис.3.3,з)
и
(рис.3.3,з)
и ![]() (рис.3.3,к)
позволяет сделать очевидный вывод о том, что если момент приводит к изгибу
какого-либо стержня, то кручение на этом участке отсутствует и наоборот.
(рис.3.3,к)
позволяет сделать очевидный вывод о том, что если момент приводит к изгибу
какого-либо стержня, то кручение на этом участке отсутствует и наоборот.
Теперь, учитывая накопленный опыт при построении эпюр от раздельного действия каждой из четырех нагрузок, рассмотрим более сложное нагружение (рис.3.3,а).
При указанных на этом рисунке нагрузках для
построения эпюры ![]() необходимо выделить 8 характерных сечений. Двигаясь от свободного конца,
получим по участкам:
необходимо выделить 8 характерных сечений. Двигаясь от свободного конца,
получим по участкам:
Участок АВ изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа:
![]()
![]() (сжаты нижние волокна).
(сжаты нижние волокна).
Кручение на участке АВ отсутствует, так как сила F и нагрузка q имеют нулевые плечи относительно продольной оси участка АВ.
Участок ВС изгибается в вертикальной плоскости, параллельной плоскости чертежа.
![]() (сжаты
верхние волокна);
(сжаты
верхние волокна);
![]() (сжаты
нижние волокна);
(сжаты
нижние волокна);
![]() , так как момент
, так как момент ![]() , приложенный к отсеченной части для сечения
5, действует в плоскости, перпендикулярной ВС и на изгиб участка ВС не влияет;
, приложенный к отсеченной части для сечения
5, действует в плоскости, перпендикулярной ВС и на изгиб участка ВС не влияет;
![]() (сжаты
нижние волокна).
(сжаты
нижние волокна).
Для построения эпюры крутящих моментов на
участке ВС рассмотрим отдельно участки 3-4 и 5-6, так как между сечениями 4 и 5
приложен момент ![]() . Участок 3-4 закручивается силой F с плечом 3м и в противоположную сторону - нагрузкой q с плечом 1,5м:
. Участок 3-4 закручивается силой F с плечом 3м и в противоположную сторону - нагрузкой q с плечом 1,5м:
![]() (здесь
знак "-" носит сугубо условный характер и
может служить только для обозначения направления кручения). Участок 5-6 помимо
силы F и
нагрузки q закручивается еще и моментом
(здесь
знак "-" носит сугубо условный характер и
может служить только для обозначения направления кручения). Участок 5-6 помимо
силы F и
нагрузки q закручивается еще и моментом ![]() , причем, в том же направлении, что и
нагрузкой q, поэтому:
, причем, в том же направлении, что и
нагрузкой q, поэтому:
![]()
Участок 7-8 закручивается нагрузкой q с плечом 2м и в противоположную сторону - силой F с плечом 2 м и моментом ![]() , следовательно:
, следовательно:
![]()
По вычисленным значениям строим эпюры ![]() и
и ![]() (рис.3.3,б).
(рис.3.3,б).
Построение эпюр в ломаных
стержнях
Систему, состоящую из жестко соединенных между собой стержней, оси которых не лежат в одной плоскости, будем называть ломаным стержнем. При этом ограничимся рассмотрением только таких ломаных стержней, отдельные элементы которых стыкуются друг с другом под прямыми углами, а внешние нагрузки приложены перпендикулярно к осям стержней (рис.3.4,а,б).
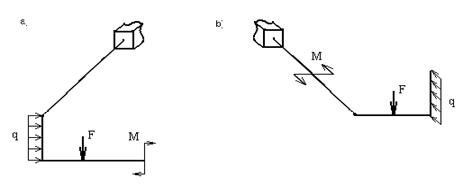
Рис.3.4
В общем случае нагружения в поперечных сечениях
ломаных стержней могут возникать все 6 известных внутренних силовых факторов:
продольная сила ![]() , поперечные силы
, поперечные силы ![]() , изгибающие моменты
, изгибающие моменты ![]() , крутящий момент
, крутящий момент ![]() . Очень часто, особенно в машиностроительных
конструкциях, отдельные элементы ломаного стержня имеют незначительную длину,
иногда соизмеримую с размерами поперечного сечения, то есть являются
"короткими" стержнями. В этом случае не только внутренние моменты
. Очень часто, особенно в машиностроительных
конструкциях, отдельные элементы ломаного стержня имеют незначительную длину,
иногда соизмеримую с размерами поперечного сечения, то есть являются
"короткими" стержнями. В этом случае не только внутренние моменты ![]() , но и внутренние силы (
, но и внутренние силы (![]() ) существенно влияют на
напряженно-деформированное состояние конструкции, поэтому для ломаных стержней
будем строить эпюры всех шести внутренних силовых факторов.
) существенно влияют на
напряженно-деформированное состояние конструкции, поэтому для ломаных стержней
будем строить эпюры всех шести внутренних силовых факторов.
Для правильного построения эпюр здесь обязательным является использование скользящей системы координат, о которой уже говорилось при рассмотрении плоско-пространственных систем.
Для обеспечения равновесия жесткого пространственного
стержня на него необходимо и достаточно наложить шесть связей; три связи,
запрещающие линейные перемещения по трем координатным осям, и три связи,
запрещающие ее поворот относительно координатных осей.
В общем случае нагружения пространственной системы
необходимо с помощью шести независимых уравнений статики определить реакции,
накладываемые внешними связями на данную систему. Методика построения эпюр
внутренних силовых факторов для пространственных систем точно такая же, как
балок и плоских рам. Сложность построения эпюр состоит только в том, что для
подсчета моментов необходимом определять плечи соответствующих сил.
Пример
2.
Рассмотрим простейший случай нагружения ломанного стержня - двумя взаимноперпендикулярными сосредоточенными силами, приложенными на свободном конце (рис.4,а).
Выбираем скользящую систему координат (рис.4,б). Ось z всегда направлена вдоль продольной оси того или иного участка ломаного стержня, а при переходе с одного участка на другой координатные оси поворачиваются на 90 градусов, но никогда не вращаются вокруг оси z. Удобнее всего начинать выбор скользящей системы координат с горизонтального участка ломаного стержня, который параллелен плоскости чертежа или лежит в этой плоскости (участок ВС на рис.4,б).
На этом участке (а он аналогичен обычной балке) ось y направляется вертикально (вверх или вниз), ось z - вдоль продольной оси участка, а ось x - перпендикулярно плоскости yoz, после чего система координат передвигается на остальные участки ломаного стержня.
Построение эпюры ![]() .
.
Построение этой и всех последующих эпюр ведем
от свободного конца. Правило знаков для ![]() остается таким же, как и для других
систем, а именно: растяжению соответствует знак "+", сжатию -
"-".
остается таким же, как и для других
систем, а именно: растяжению соответствует знак "+", сжатию -
"-".
Участок АВ имеет нулевую
продольную силу, так как ![]() перпендикулярны продольной оси этого участка:
перпендикулярны продольной оси этого участка:
![]()
Участок ВС растягивается силой ![]() :
:
![]()
Участок СД сжимается силой ![]() :
:
![]()
Построение эпюр ![]() и
и ![]() .
.
Поперечную силу ![]() формируют только те силы, которые параллельны
оси x на данном участке, а поперечную силу
формируют только те силы, которые параллельны
оси x на данном участке, а поперечную силу ![]() - силы, параллельные оси y. Здесь также
сохраняется обычное для Q правило знаков:
- силы, параллельные оси y. Здесь также
сохраняется обычное для Q правило знаков: ![]() , если внешняя сила, приложенная к отсеченной
части, стремится повернуть рассматриваемое сечение по часовой стрелке и
, если внешняя сила, приложенная к отсеченной
части, стремится повернуть рассматриваемое сечение по часовой стрелке и ![]() - в
противоположном случае. С учетом сказанного в характерных сечениях имеем:
- в
противоположном случае. С учетом сказанного в характерных сечениях имеем:
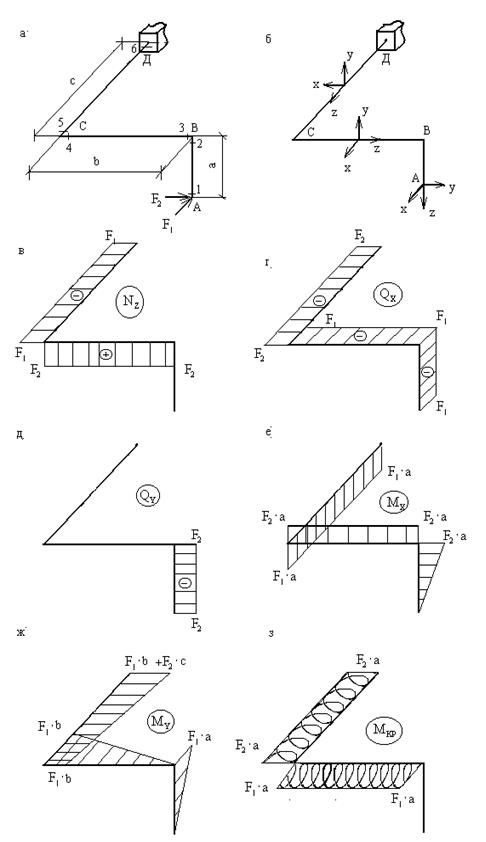
Рис. 4
![]()
![]()
![]()
![]()
![]()
Построение эпюр ![]() .
.
Ординаты эпюр изгибающих моментов будем, как обычно,
откладывать со стороны сжатых волокон, не указывая знаков, причем ориентировать
эпюры нужно так, чтобы плоскость эпюры совпадала с плоскостью действия пары
того изгибающего момента, для которого она построена. Иначе говоря, эпюра ![]() на
всех участках ломаного стержня располагается в плоскости yoz, а эпюра
на
всех участках ломаного стержня располагается в плоскости yoz, а эпюра ![]() - в плоскости xoz.
- в плоскости xoz.
Начнем с построения эпюры ![]() . Здесь нас будет интересовать изгиб каждого
участка в плоскости yoz (см. скользящую систему координат на рис.4,б) и,
соответственно, плечо каждой действующей на отсеченную часть нагрузки нужно
измерять в этой плоскости.
. Здесь нас будет интересовать изгиб каждого
участка в плоскости yoz (см. скользящую систему координат на рис.4,б) и,
соответственно, плечо каждой действующей на отсеченную часть нагрузки нужно
измерять в этой плоскости.
На участке АВ плоскость yoz
- вертикальная плоскость, параллельная плоскости чертежа. В этой плоскости
стержень АВ изгибается только силой ![]() , так как
, так как ![]() перпендикулярна плоскости yoz :
перпендикулярна плоскости yoz :
![]()
![]() (сжаты
правые волокна).
(сжаты
правые волокна).
На участке ВС плоскость yoz ориентирована так же, как и на участке АВ,
причем, все точки ВС равноудалены от линии действия силы ![]() , поэтому:
, поэтому:
![]() (сжаты
верхние волокна).
(сжаты
верхние волокна).
На участке СД плоскость yoz
- вертикальная плоскость, перпендикулярная плоскости чертежа. В этой плоскости
стержень СД изгибается только силой ![]() , так как
, так как ![]() перпендикулярна yoz ;
все точки участка СД равноудалены (в рассматриваемой плоскости) от линии действия
силы
перпендикулярна yoz ;
все точки участка СД равноудалены (в рассматриваемой плоскости) от линии действия
силы ![]() , следовательно:
, следовательно:
![]() (сжаты
нижние волокна).
(сжаты
нижние волокна).
Рассуждая аналогичным образом, будем строить
эпюру ![]() , но теперь нужно рассматривать изгиб каждого
участка ломаного стержня в плоскости xoz.
, но теперь нужно рассматривать изгиб каждого
участка ломаного стержня в плоскости xoz.
На участке АВ плоскость xoz
- вертикальная плоскость, перпендикулярная плоскости чертежа. В этой плоскости
стержень АВ изгибается только силой ![]() , так как
, так как ![]() перпендикулярна плоскости xoz:
перпендикулярна плоскости xoz:
![]()
![]() (сжаты
дальние от наблюдателя волокна).
(сжаты
дальние от наблюдателя волокна).
На участке ВС плоскость xoz
- горизонтальная плоскость. В этой плоскости сила ![]() приложена вдоль продольной оси стержня ВС и к
изгибу привести не может, поэтому:
приложена вдоль продольной оси стержня ВС и к
изгибу привести не может, поэтому:
![]()
![]() (сжаты
дальние от наблюдателя волокна).
(сжаты
дальние от наблюдателя волокна).
На участке СД плоскость xoz
- это так же горизонтальная плоскость. Здесь к изгибу стержня СД приводят обе
силы: плечо силы ![]() постоянно и равно b, а плечо силы
постоянно и равно b, а плечо силы ![]() равно
нулю в сечении 5 и равно с в сечении 6:
равно
нулю в сечении 5 и равно с в сечении 6:
![]()
Иногда при построении эпюр изгибающих
моментов в ломанных стержнях возникают затруднения в
определении участия той или иной нагрузки в изгибе стержня или в определении
плеча той или иной нагрузки. В этих случаях всегда можно использовать простой,
но эффективный прием: спроектировать конструкцию и действующие нагрузки на ту плоскость в которой изгибается стержень, переходя тем самым
от пространственной конструкции к ее проекции, что позволяет легко определить
плечи каждой из нагрузок и их "вклад" в изгиб рассматриваемого
участка. Проследим использование этого приема например, при построении эпюры ![]() на
участке СД (рис.4,а,б). На этом участке плоскость xoz,
в которой нужно рассматривать изгиб стержня при построении
на
участке СД (рис.4,а,б). На этом участке плоскость xoz,
в которой нужно рассматривать изгиб стержня при построении ![]() - горизонтальная плоскость, следовательно,
для реализации описываемого приема необходимо спроектировать конструкцию на
горизонтальную плоскость, то есть изобразить вид сверху (рис.5).
- горизонтальная плоскость, следовательно,
для реализации описываемого приема необходимо спроектировать конструкцию на
горизонтальную плоскость, то есть изобразить вид сверху (рис.5).
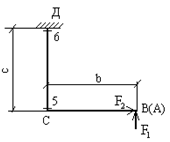
Рис.5
При этом сила ![]() будет видна направленной вдоль стержня ВС,
сила
будет видна направленной вдоль стержня ВС,
сила ![]() - перпендикулярно ВС, а
стержень ВА проектируется в точку. Теперь совершенно очевидно, что все
точки стержня СД равноудалены от линии действия силы
- перпендикулярно ВС, а
стержень ВА проектируется в точку. Теперь совершенно очевидно, что все
точки стержня СД равноудалены от линии действия силы ![]() , что приводит к постоянному моменту
, что приводит к постоянному моменту ![]() , а сила
, а сила ![]() имеет
нулевое плечо в сечении 5 и плечо, равное с, - в
сечении 6:
имеет
нулевое плечо в сечении 5 и плечо, равное с, - в
сечении 6:
![]()
![]()
В обоих сечениях сжаты правые волокна, то есть получен тот же результат, что и ранее, но в более наглядном виде.
Пример
3.
Построить эпюры изгибающих и крутящих моментов для
пространственного ломанного стержня, показанного на
рис.5.1,а.
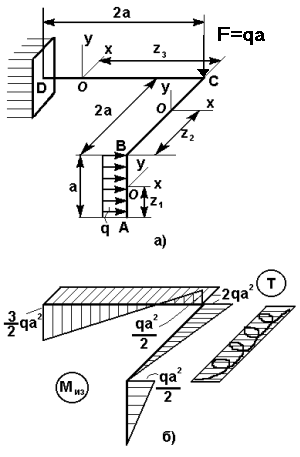
Рис.5.1
Стержень состоит из трех прямых брусьев АВ, ВС, СД,
жестко соединенных под прямыми углами в узлах В и С. Брус
АВ расположен в вертикальной плоскости, брусья ВС и СД - в горизонтальной плоскости.
Для определения внутренних силовых факторов,
действующих в поперечных сечениях стержня, воспользуемся методом сечений.
Рассекаем участок АВ на расстоянии Z1 от свободного
торца А (рис. 5.1,а)
и проводим оси координат в поперечном сечении бруса, поместив начало координат
в центре тяжести поперечного сечения бруса.
Ось Z направляем по нормали к поперечному сечению, а
оси X и Y проведём в плоскости поперечного сечения.
Определяем моменты относительно каждой оси. Равномерно
распределенная нагрузка заменяется равнодействующей qZ1
Эта равнодействующая параллельна оси X, поэтому MX=0.
Относительно оси Y плечом для равнодействующей qZ1 будет расстояние
между плоскостью XOY и параллельной ей горизонтальной плоскостью, содержащей
равнодействующую qZ1. Это расстояние ![]() .
.
![]()
Изгибающий момент меняется по параболе от нуля (при Z1=0)
до ![]() ( при Z1=a). (Сжаты
волокна правой половины поперечного сечения бруса). Момент относительно оси Z
равен нулю, т.к. равнодействующая qZ1, пересекает ось Z.
( при Z1=a). (Сжаты
волокна правой половины поперечного сечения бруса). Момент относительно оси Z
равен нулю, т.к. равнодействующая qZ1, пересекает ось Z.
Переходим к участку ВС.
Проводим сечение на расстоянии Z2 от
сечения В (рис.5.1,а).
Таким же образом, как и на участке АВ, проводим оси координат.
Равномерно распределённая нагрузка заменяется
равнодействующей qa, ![]() , т.к.
равнодействующая qa параллельна
оси X
, т.к.
равнодействующая qa параллельна
оси X ![]()
![]() - плечо для
равнодействующей qa, определяется
как расстояние между вертикальной плоскостью YOZ и параллельной ей вертикальной
плоскостью, содержащей равнодействующую qa (сжаты волокна
правой половины поперечного сечения бруса),
- плечо для
равнодействующей qa, определяется
как расстояние между вертикальной плоскостью YOZ и параллельной ей вертикальной
плоскостью, содержащей равнодействующую qa (сжаты волокна
правой половины поперечного сечения бруса),
При Z2=0 MY=0
При Z2=2а MY=2qa2
![]()
![]() - плечо для равнодействующей qa.
- плечо для равнодействующей qa.
Определяемое как расстояние между плоскостью ZOX и
параллельной ей горизонтальной плоскостью, содержащей равнодействующую qa.
Рассмотрим участок СД
По аналогии с предыдущими участками рассечём брус СД на расстоянии Z3 от сечения С. Проводим
оси X1Y1Z и определяем моменты относительно этих осей.
Относительно оси X создают момент сила F=qa и
равнодействующая на участке АВ, равная qa.
Плечом для силы F является расстояние между плоскостью XOY и параллельной ей
вертикальной плоскостью, содержащей силу F. Это расстояние равно Z3. Плечом для
равнодействующей qa
является расстояние между плоскостью XOZ и параллельной ей горизонтальной
плоскостью, содержащей силу qa.
Это расстояние - a/2. Итак, ![]() (Момент, сжимающий верхнюю половину
поперечного сечения бруса, взят со знаком плюс).
(Момент, сжимающий верхнюю половину
поперечного сечения бруса, взят со знаком плюс).
При ![]() (сжато
верхнее волокно);
(сжато
верхнее волокно);
При ![]() (сжато
нижнее волокно бруса);
(сжато
нижнее волокно бруса);
Плечом силы ![]() (равнодействующей на участке АВ) относительно
оси Y будет расстояние между плоскостью YOZ и параллельной ей вертикальной
плоскостью, содержащей равнодействующую
(равнодействующей на участке АВ) относительно
оси Y будет расстояние между плоскостью YOZ и параллельной ей вертикальной
плоскостью, содержащей равнодействующую![]() . Это расстояние равно 2a.
. Это расстояние равно 2a. ![]() (сжато
заднее волокно). Сила F=qa
момента относительно оси Y не дает т.к. сила параллельна оси Y.
(сжато
заднее волокно). Сила F=qa
момента относительно оси Y не дает т.к. сила параллельна оси Y. ![]() , т.к. сила F - пересекает ось Z, а равнодействующая
, т.к. сила F - пересекает ось Z, а равнодействующая ![]() на
участке АВ – параллельна оси Z. Эпюры изгибающих и крутящих моментов приведены
на рис.5.1,б. Эпюра изгибающих
моментов построена на сжатых волокнах. Нетрудно подметить, что при построении
эпюр моментов, пользуясь методом сечений, всё время рассматривалось равновесие
той части рамы, которая не содержит опорных реакций, что позволило не
определять их.
на
участке АВ – параллельна оси Z. Эпюры изгибающих и крутящих моментов приведены
на рис.5.1,б. Эпюра изгибающих
моментов построена на сжатых волокнах. Нетрудно подметить, что при построении
эпюр моментов, пользуясь методом сечений, всё время рассматривалось равновесие
той части рамы, которая не содержит опорных реакций, что позволило не
определять их.
Расчет на прочность и подбор
сечения ломаных пространственных стержней
В общем случае сложного сопротивления в стержне возникают все шесть видов внутренних усилий одновременно. Эти шесть усилий определяем, как обычно, методом сечений и строим эпюры усилий. После определения внутренних усилий находим опасные сечения, а в опасных сечениях – опасные точки. Рассмотрим подробно, где расположены опасные точки в двух наиболее часто используемых сечениях: круглом и прямоугольном. Выпишем формулы, необходимые для проверки прочности в этих точках.
Для определения положения опасных точек в круглом сечении построим эпюры
распределения напряжений. Чтобы построить эпюру нормальных
напряжений, вызванных двумя изгибающими моментами ![]() и
и ![]() определим направление суммарного
изгибающего момента. Изобразим пары
определим направление суммарного
изгибающего момента. Изобразим пары ![]() и
и ![]() в виде
векторов, определяя их направление по правилу правого винта (рис. 6).
в виде
векторов, определяя их направление по правилу правого винта (рис. 6).
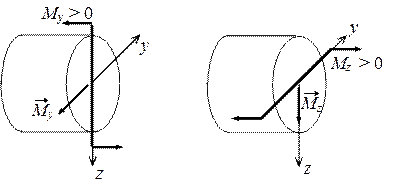
Рис.6
Полный изгибающий момент является
равнодействующей этих векторов и изображен на рис.2. Поскольку для круглого
сечения любая ось является главной, то в какой бы плоскости не был приложен
изгибающий момент, он вызывает плоский изгиб. Нейтральная
линия в этом случае перпендикулярна плоскости изгиба, то есть совпадает с
линией действия вектора полного изгибающего момента ![]() . На рис. 7 показана эпюра
нормальных напряжений, вызванных действием изгибающего момента
. На рис. 7 показана эпюра
нормальных напряжений, вызванных действием изгибающего момента ![]() . Кроме того, в сечении возникают
нормальные напряжения от продольной силы N и касательные
напряжения от крутящего момента
. Кроме того, в сечении возникают
нормальные напряжения от продольной силы N и касательные
напряжения от крутящего момента ![]() Эпюры распределения этих напряжений показаны
на рис. 7. Знаки напряжений
соответствуют положительным значениям внутренних усилий. Видно, что опасными точками
могут быть точки 1, 1¢, в которых действуют максимальные нормальные
напряжения от изгиба и продольной силы и максимальные касательные напряжения,
вызванные крутящим моментом. Для проверки прочности хрупких материалов важен
знак нормальных напряжений (более опасной точкой будет, как правило, точка с
растягивающими напряжениями), для пластичных материалов опасной будет точка,
где нормальные напряжения от изгиба и продольной силы имеют одинаковые знаки.
Опасные точки находятся в "балочном" напряженном состоянии и проверку
прочности в них следует осуществлять по теориям прочности, соответствующим
материалу стержня. Приведем условия прочности, справедливые для
"балочного" напряженного состояния, по двум наиболее часто
используемым теориям:
Эпюры распределения этих напряжений показаны
на рис. 7. Знаки напряжений
соответствуют положительным значениям внутренних усилий. Видно, что опасными точками
могут быть точки 1, 1¢, в которых действуют максимальные нормальные
напряжения от изгиба и продольной силы и максимальные касательные напряжения,
вызванные крутящим моментом. Для проверки прочности хрупких материалов важен
знак нормальных напряжений (более опасной точкой будет, как правило, точка с
растягивающими напряжениями), для пластичных материалов опасной будет точка,
где нормальные напряжения от изгиба и продольной силы имеют одинаковые знаки.
Опасные точки находятся в "балочном" напряженном состоянии и проверку
прочности в них следует осуществлять по теориям прочности, соответствующим
материалу стержня. Приведем условия прочности, справедливые для
"балочного" напряженного состояния, по двум наиболее часто
используемым теориям:
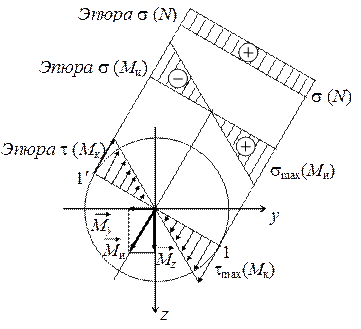
Рис.7
- для хрупких материалов – теория Мора
![]()
где ![]()
![]()
- для пластичных материалов – третья теория прочности
![]()
В формулах (1), (2) ![]() и
и ![]() –
напряжения в опасных точках.
–
напряжения в опасных точках.
В точках 1, 1¢ круглого сечения эти напряжения определяются так:
![]()
![]()
![]()
![]()
![]()
При подборе сечения обычно пренебрегают влиянием продольной силы. В этом случае условия прочности (1) и (2) для круглого сечения с учетом формул (5) и (6) можно преобразовать. Теория Мора приобретает такой вид:
![]()
а третья теория прочности приводится к следующему условию:
![]()
где ![]()
Из условий прочности (7), (8) можно найти необходимый момент сопротивления, а далее радиус поперечного сечения. Чтобы учесть продольную силу, немного увеличивают полученное значение радиуса (как правило, достаточно округления в большую сторону), находят напряжения по формулам (4)–(6) и проверяют прочность с учетом N по условиям (1) или (2).
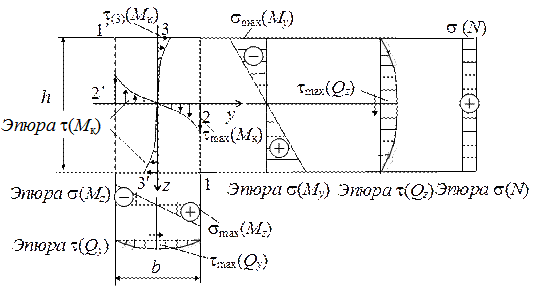
Рис.8
Построим эпюры распределения напряжений от всех усилий в прямоугольном сечении и определим положение опасных точек. Эти эпюры изображены на рис. 8, где знаки и направления напряжений соответствуют положительным внутренним усилиям. Из рис. 8 следует, что в прямоугольном сечении в общем случае опасными могут быть три группы точек:
- точки 1, 1¢ с максимальными нормальными напряжениями (для хрупких материалов важна не только величина напряжения, но и его знак).
![]()
- точки 2, 2¢ – в них действуют нормальные напряжения от N, максимальные нормальные напряжения от
![]() и максимальные касательные напряжения, вызванные крутящим
моментом и поперечной силой
и максимальные касательные напряжения, вызванные крутящим
моментом и поперечной силой ![]() :
:
![]()
![]()
- точки 3, 3¢ с нормальными напряжениями от N, максимальными нормальными напряжениями от
![]() и, кроме того, в этих точках действуют касательные напряжения
от кручения и максимальные касательные напряжения, вызванные поперечной силой
и, кроме того, в этих точках действуют касательные напряжения
от кручения и максимальные касательные напряжения, вызванные поперечной силой ![]() :
:
![]()
![]()
В зависимости от величин и знаков внутренних
усилий необходимо выбрать самые опасные точки и проверить в них прочность.
Знаки "плюс" или "минус" в формулах (9) – (13) выбираются в
зависимости от направления напряжений в рассматриваемой точке. При этом в
точках 2, 2¢ или 3, 3¢ хотя бы для одного напряжения ( ![]() или
или ![]() ) направления должны совпадать.
) направления должны совпадать.
В точке 1, где нормальные напряжения от N, ![]() и
и ![]() имеют
один знак, условие прочности записывается так
имеют
один знак, условие прочности записывается так
![]()
так как эта точка находится в линейном
напряженном состоянии. Для хрупких материалов в правой части неравенства стоит ![]() или
или ![]() в
зависимости от направления напряжения. Точки 2 (2¢) и 3 (3¢) находятся в "балочном" напряженном
состоянии и условие прочности в них записывается по формулам (1) или (2) в
зависимости от материала.
в
зависимости от направления напряжения. Точки 2 (2¢) и 3 (3¢) находятся в "балочном" напряженном
состоянии и условие прочности в них записывается по формулам (1) или (2) в
зависимости от материала.
В формулах (9) – (13)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Коэффициенты ![]() и
и ![]() определяются по таблице и зависят от h/b. В приведенных формулах b – меньшая сторона
прямоугольника, параллельная оси y. Знаки усилий в
формулах (4)–(6) и (15)–(20) не учитываются.
определяются по таблице и зависят от h/b. В приведенных формулах b – меньшая сторона
прямоугольника, параллельная оси y. Знаки усилий в
формулах (4)–(6) и (15)–(20) не учитываются.
Подбор размеров прямоугольного сечения производят из условия прочности в угловой точке без учета продольной силы. Условие прочности (8) в этой точке преобразуется к следующему виду:
![]()
Зная отношение моментов сопротивления ![]() , из (21) можно найти необходимую величину
момента сопротивления, а далее размеры сечения. Для учета продольной силы
обычно округляют полученные размеры в большую сторону и проверяют прочность во
всех опасных точках прямоугольного сечения с учетом всех усилий по приведенным
выше формулам.
, из (21) можно найти необходимую величину
момента сопротивления, а далее размеры сечения. Для учета продольной силы
обычно округляют полученные размеры в большую сторону и проверяют прочность во
всех опасных точках прямоугольного сечения с учетом всех усилий по приведенным
выше формулам.
Пример 4.
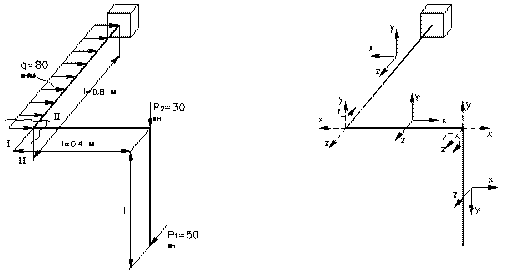
Задан стержень пространственного очертания, загруженный нагрузками (рис.9, а). Для заданного материала стержня требуется подобрать размеры поперечного сечения наиболее опасного участка для двух вариантов сечения: круглого и прямоугольного.
Рис.9
Решение.
Определим внутренние усилия, используя метод сечений и правила знаков для усилий, справедливые для всех задач сложного сопротивления (см. рис. 10).
Рис. 10
На каждом участке введем местные системы координат, показанные на рис. 2, б. Ось х всегда направлена вдоль оси стержня, оси y, z – главные центральные оси инерции сечения. Чтобы не определять опорные реакции, будем рассматривать все силы со свободного конца стержня и найдем усилия в сечениях 0–5 (см. рис. 10, б).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В соответствии с полученными результатами построим эпюры внутренних усилий (рис. 11).
Рис.11
В рассматриваемом примере опасным является
участок длиной ![]() , где действуют все усилия. На этом участке
опасным будем считать сечение 5 (хотя при определенном сочетании величин
нагрузок и размеров может быть опасным и сечение 4). Считая, что материал
стержня – чугун (
, где действуют все усилия. На этом участке
опасным будем считать сечение 5 (хотя при определенном сочетании величин
нагрузок и размеров может быть опасным и сечение 4). Считая, что материал
стержня – чугун (![]() ) подберем размеры поперечного сечения
стержня, приняв следующие исходные данные:
) подберем размеры поперечного сечения
стержня, приняв следующие исходные данные: ![]() . Для этих данных в
опасном сечении 5 действуют такие усилия:
. Для этих данных в
опасном сечении 5 действуют такие усилия:
![]()
![]()
Рассмотрим первый вариант – стержень круглого поперечного сечения. Подбор радиуса сечения производим без учета продольной и поперечных сил в соответствии с заданным материалом из условия прочности по теории Мора
![]()
В этой формуле
![]()
![]()
Из условия прочности по теории Мора найдем необходимый момент сопротивления
![]()
откуда, вспомнив, что ![]() , найдем радиус сечения
, найдем радиус сечения
![]()
Округляя радиус в большую сторону, примем r=7,9 см.
Далее необходимо построить эпюры распределения напряжений в круглом поперечном сечении. Для рассматриваемого примера эти эпюры показаны на рис. 12.
Рис.12
Напряжения определены по формулам
![]()
![]()
![]()
Сделаем проверку прочности для найденного размера с учетом продольной силы. Для чугунного стержня опасной является точка, в которой действуют растягивающие нормальные напряжения, т. е. точка 1 на рис. 12. В этой точке
![]() кН/см2;
кН/см2;
![]() кН/см2.
кН/см2.
Подставим найденные напряжения в условие прочности по теории Мора
![]()
![]()
Таким образом, найденный радиус r=7,9 см удовлетворяет условию прочности с учетом продольной силы и является окончательным.
Теперь рассмотрим второй вариант – стержень прямоугольного сечения с отношением h/b=2. Подбор сечения производим из условия прочности ![]() в угловой точке сечения. Поскольку в рассматриваемом примере
в угловой точке сечения. Поскольку в рассматриваемом примере ![]() , то располагаем сечение выгодным образом,
т.е. так, чтобы ось y располагалась посередине длинной стороны h прямоугольника. Тогда
, то располагаем сечение выгодным образом,
т.е. так, чтобы ось y располагалась посередине длинной стороны h прямоугольника. Тогда ![]() и
условие
и
условие ![]() для чугуна перепишем в таком виде:
для чугуна перепишем в таком виде:
![]()
Отсюда получим необходимый момент сопротивления
![]()
и, учтя, что ![]() , найдем высоту сечения
, найдем высоту сечения
![]()
Построим эпюры распределения напряжений в прямоугольном сечении от всех видов внутренних усилий и проверим прочность во всех опасных точках. Эпюры напряжений и опасные точки для рассматриваемого примера показаны на рис. 13.
Рис.13
Напряжения найдены по формулам
![]()
![]()
![]()
![]()
![]()
![]()
Опасными для хрупкого материала являются точки, в которых действуют растягивающие напряжения, т.е. точки 1, 2 и 3 (см. рис. 13). Суммируем напряжения в опасных точках с учетом их направлений. В точке 1
![]()
то есть условие прочности выполняется.
В точке 2
![]() кН/см2,
кН/см2,
![]() кН/см2
кН/см2
и условие прочности по теории Мора
![]()
выполняется.
Наконец, в точке 3 действуют напряжения
![]() кН/см2,
кН/см2,
![]() кН/см2.
кН/см2.
Условие прочности в этой точке
![]()
тоже выполняется. Таким образом, найденные размеры поперечного сечения h=20,4 см и b=10,2 см удовлетворяют условиям прочности во всех опасных точках.
Пример 5.
Дан пространственный консольный брус с ломаным очертанием осевой линии, нагруженный сосредоточенной силой Р = 1 кН и равномерно распределенной нагрузкой q = 2 кН/м. На рис. 14, а этот брус показан в аксонометрии в соответствии с прямоугольной системой координат xyz . Вертикальный элемент бруса имеет поперечное сечение в виде круга диаметром d = 0,06 м (рис. 1, в), горизонтальные элементы бруса имеют поперечные сечения в виде прямоугольника (рис. 14, б). Ширина сечения b = d = 0,06 м, а высота сечения c = 0,5d = 0,03 м. Ориентация главных осей поперечных сечений на каждом участке показана на рис. 14, г.
Требуется:
1. Построить в аксонометрии эпюры Mx , My , Mz , Nz, Qx , Qy ;
2. Указать вид сопротивления для каждого участка бруса;
3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий Nz, Mx , My и Mz (касательными напряжениями от Qx и Qy можно пренебречь);
4. Проверить прочность при расчетном сопротивлении R = 180 МПа.

Рис.14
Решение.
1. Построить в аксонометрии эпюры Mx , My , Mz , Nz, Qx , Qy . Заметим, что так как заданная система пространственная, при произвольном характере нагружения, в опорном сечении, где установлена заделка, возникает шесть опорных реакций (три опорные силы и три момента). Для определения опорных реакций, в данном случае, можем применить шесть уравнений равновесия статики. Так как число независимых уравнений равновесия равно числу опорных реакций, то можно сделать вывод, что рассматриваемая система в виде ломаного бруса, с заделанным одним концом, является статически определимой. Поэтому рассматриваемая система разрешима по методу сечений. Далее, учитывая особенности конструкции, определение величин внутренних усилий можно осуществить без предварительного вычисления величин опорных реакций.
Брус имеет три участка АВ, ВС и СD (рис. 14, г). При этом, после рассечения бруса на две части будем рассматривать равновесие оставшейся части, не связанной с заделкой (чтобы избежать предварительного определения опорных реакций в заделке бруса). Внутренние силовые факторы можно рассматривать как реакции, действующие в сечении на оставшуюся часть со стороны отброшенной части, поэтому процесс определения шести величин Mx , My , Mz , Nz, Qx , Qy может быть сведен к известному процессу определения опорных реакций.
Следует отметить, что при определении опорных реакций их направление можно указать произвольно, а затем из решения уравнения равновесия будет ясно, как в действительности действует реакция: если результат положительный, то реакция действует именно так, как мы предварительно указали, если отрицательный - то наоборот.
При построении эпюр будем руководствоваться следующими правилами:
- нормальная сила Nz считается положительной, если она вызывает растяжение бруса;
- крутящий момент Mz считается положительным, если при взгляде на сечение со стороны внешней нормали он виден вращающим брус по ходу часовой стрелки;
- поперечная сила Qx считается положительной, если при взгляде со стороны положительного направления оси y она стремится вращать оставшуюся часть бруса по ходу часовой стрелки относительно ближайшей точки на оси бруса (для поперечной силы Qy - то же, по отношению к x);
- ординаты эпюр Qx и Qy следует откладывать перпендикулярно оси бруса в плоскости действия этих сил и указывать знак;
- ординаты эпюр Мx и Мy будем откладывать перпендикулярно оси бруса со стороны растянутого волокна.
Участок АВ
(![]() ).
).
Оставшаяся часть изображена на
рис. 14, д. В центре
сечения помещаем систему координат. Оси x
и y совпадают с направлением главных
осей инерции сечения, показанных на рис. 14, г. Координата z1
увеличивается от точки А
к точке В. Для определения N покажем ее в направлении от сечения,
т.е. растягивающей, и составим уравнения равновесия: ![]() Nz = 0. Из
Nz = 0. Из ![]() следует Мx = 0
(рис. 15, а).
следует Мx = 0
(рис. 15, а).
Для определения Мz покажем его так, чтобы при взгляде на сечение он был виден вращающим брус по часовой стрелке, и составим уравнения равновесия (рис. 15, б):
![]() ; Мz = 0.
; Мz = 0.
Для определения Qx и Qy покажем их положительными в соответствии с выбранным правилом знаков и составим уравнения равновесия:
![]() , Qx - P = 0, Qx = P = 1 кН;
, Qx - P = 0, Qx = P = 1 кН;
![]() , Qy =
0.
, Qy =
0.
Эпюра Qx представляет собой прямоугольник (рис. 15, в) с ординатой, равной 1, лежащей в плоскости действия этого силового фактора. Составляем уравнение равновесия:
![]()
Ординаты эпюры My линейно зависят от z:
z = 0, My = 0;
z = a, My = -Pa = -1![]() 0,3 = -0,3 кНм.
0,3 = -0,3 кНм.
Знак минус указывает на то, что в действительности изгибающий момент My вызывает растягивающее напряжение в правой части поперечного сечения, поэтому ординаты эпюры My откладываются в правую сторону.
Участок ВC (![]() ).
).
Оставшаяся часть изображена на рис. 14, e. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 14, г. Координата z2 увеличивается от точки В к точке С. Процесс определения внутренних силовых факторов на этом участке такой же, как и на предыдущем. Важно отметить, что на оставшейся части соответствующий внутренний силовой фактор удобно показывать непосредственно перед его определением - для того, чтобы не затемнить чертеж. При этом Nz, Mz , Qx , Qy показывают в положительном направлении в соответствии с принятым правилом знаков, а изгибающие моменты Mx и My - наугад из двух возможных направлений (рис.14, e):
![]() , Nz = 0;
, Nz = 0;
![]() Mz + Pa = 0, Mz = -Pa = -0,3 кНм.
Mz + Pa = 0, Mz = -Pa = -0,3 кНм.
Плоскость прямоугольной эпюры произвольна (рис. 15, б).
![]() , Qx - P = 0,
Qx = P = 1 кН.
, Qx - P = 0,
Qx = P = 1 кН.
Эпюра Qx в виде прямоугольника показана на рис. 15, в.
![]() , Qy - q z = 0; Qy = q z ;
, Qy - q z = 0; Qy = q z ;
z = 0, Qy = 0;
z = 0,6
м, Qy = 2![]() 0,6 = 1,2 кН.
0,6 = 1,2 кН.
Эпюра Qy в виде треугольника показана на рис. 15, е.
![]()

Рис.15
Ординаты Mx изменяются по закону квадратной параболы.
z = 0, Mx = 0;
z = 0,6 м, Mx = -0,36 кНм;
![]() ; z = 0- точка экстремума в эпюре Mx в сечении z = 0.
; z = 0- точка экстремума в эпюре Mx в сечении z = 0.
Знак минус указывает, что растягивающие
напряжения возникают не в ближней части сечения, а в дальней. При этом наблюдатель
ориентирован относительно глобальной системы координат xy, показанной на рис. 14, а следующим образом: ось x направлена к наблюдателю, поэтому
ординаты Mx
откладываем в дальнюю сторону (рис. 15, а).
![]() , My + P z = 0, My = -P z;
, My + P z = 0, My = -P z;
z = 0, My = 0;
z = 0,6 м, My = -0,6 кНм.
Эпюра My - треугольная. Растягивающие напряжения возникают в правой части сечения - ординаты откладываем вправо.
Участок CD
(![]() ).
).
Оставшаяся часть изображена на рис. 14, ж. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 14, г. Координаты z3 увеличиваются от точки С к точке D. Повторяя все рассуждения, проведенные на предыдущих участках, будем иметь следующее (рис. 14, д):
![]() , N - P = 0, N = P = 1 кН;
, N - P = 0, N = P = 1 кН;
![]() кНм.
кНм.
Эпюра Mz - в виде прямоугольника. Плоскость изображения произвольная:
![]() , Qx + q b1 = 0, Qx = -q b1 = -2
, Qx + q b1 = 0, Qx = -q b1 = -2![]() 0,6= -1,2 кН.
0,6= -1,2 кН.
Эпюра Qx - в виде прямоугольника в плоскости действия Qx.
![]() , Qy = 0;
, Qy = 0;
![]() , Mx + P b1 = 0,
Mx
= -P b1 = -0,6 кНм.
, Mx + P b1 = 0,
Mx
= -P b1 = -0,6 кНм.
Эпюра Mx - в виде прямоугольника. Растягивающие напряжения при изгибе возникают в нижней части поперечного сечения -ординаты эпюры откладываем вниз.
![]() , My + P a - q b1 z3 = 0,
My = q b1 z3 -P a = 1,2 z3 - 0,3.
, My + P a - q b1 z3 = 0,
My = q b1 z3 -P a = 1,2 z3 - 0,3.
Величина My определяется как линейная функция от z3. При z3 = 0; My = -0,3 кНм. В этом сечении растягивающие напряжения возникают не в дальней части сечений, а в ближней - ординату откладываем к наблюдателю.
При z3 = 0,5м My = 1,2![]() 0,5 - 0,3 = 0,6-0,3 = 0,3 кНм.
0,5 - 0,3 = 0,6-0,3 = 0,3 кНм.
В этом сечении My откладываем от наблюдателя (рис. 15, г).
2. Установить вид сопротивления для каждого участка бруса. По эпюрам устанавливаем вид сопротивления на каждом участке бруса. На участке АВ возникают изгибающий момент My и поперечная сила Qx , что свидетельствует о наличии поперечного изгиба. На участке ВС возникают изгибающие моменты Mx, My , поперечные силы Qx , Qy и крутящий момент Mx , что свидетельствует о наличии косого изгиба и кручения. На участке СD действуют изгибающие моменты Mx и My , поперечная сила Qx , растягивающая сила N и крутящий момент Mz , что свидетельствует о наличии косого изгиба с растяжением и кручением.
3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N, Mx, My и Mz (касательными напряжениями от Qx и Qy можно пренебречь). Участок АВ. Наибольшая величина изгибающего момента My , судя по эпюре (рис. 2, г) возникает в сечении, бесконечно близком к точке В. Максимальные нормальные напряжения при изгибе определяются по формуле:
![]()
где момент сопротивления
![]()
Участок ВС. По эпюрам Mx и My устанавливаем, что опасным является сечение, бесконечно близкое к точке С. Для круглого сечения суммарный изгибающий момент:
![]() кНм,
кНм,
а наибольшие нормальные напряжения равны:
![]()
где момент сопротивления круглого сечения при изгибе:
![]()
При кручении круглого сечения возникают касательные напряжения, максимальные значения которых определяются по формуле:
![]()
где Wp - момент сопротивления при кручении. Известно, что
![]()
тогда
![]()
Участок СD. По эпюрам Mx и My видим, что равными по опасности будут сечения, бесконечно близкие к точкам С и D. При действии растягивающей силы N во всех точках поперечного сечения возникают одинаковые нормальные напряжения:
![]()
где F = b![]() c = 0,06
c = 0,06![]() 0,03=0,0018 м2 - площадь поперечного сечения;
0,03=0,0018 м2 - площадь поперечного сечения;
![]()
где
![]()
При действии изгибающего момента My наибольшие нормальные напряжения будут равны:
![]()
При кручении бруса прямоугольного сечения возникают касательные напряжения, максимальные значения которых определятся по формуле:
![]()
где ![]() - геометрическая величина, играющая роль момента
сопротивления при кручении стержней прямоугольного сечения. Здесь
- геометрическая величина, играющая роль момента
сопротивления при кручении стержней прямоугольного сечения. Здесь ![]() - коэффициент, зависящий от отношения большей
стороны прямоугольника к меньшей (в данном случае при b/c
= 2,
- коэффициент, зависящий от отношения большей
стороны прямоугольника к меньшей (в данном случае при b/c
= 2, ![]() = 0,493).
= 0,493).
4. Проверка прочности при расчетным сопротивлении R = 180 МПа. Расчетное напряжение по третьей теории прочности для плоского напряженного состояния определяется по формуле:
![]()
Участок АВ. Линейное напряженное
состояние является частным случаем плоского (![]() ), поэтому в нашем случае:
), поэтому в нашем случае:
![]() где R = 180 МПа.
где R = 180 МПа.
Участок ВС. Проверка прочности по третьей теории:
![]()
Участок СD. Сначала найдем максимальное нормальное напряжение от внутренних силовых факторов N, Mx и My :
![]()
Касательные напряжения в угловой точке от кручения равны 0. Имеет место линейное напряженное состояние:
![]()
Далее рассмотрим напряженное состояние в
окрестности точки, где действует максимальное касательное напряжение ![]() = 27,7 МПа. Имеет место
плоское напряженное состояние:
= 27,7 МПа. Имеет место
плоское напряженное состояние:
![]()
![]()
Следовательно, так как условие обеспечения прочности во всех опасных точках участков ломанного бруса выполняются, то прочность конструкции в целом следует считать обеспеченной.
Пример 6.
Определить из расчета на прочность диаметр d сечения пространственной рамы (рис. 16, а), применив критерий Мизеса. Дано:
![]()
а)
б)
Рис.16
Решение.
Так как рама консольная, то эпюры внутренних
силовых факторов строим без определения
опорных реакций. Как и ранее, направим ось z на первом стержне по его оси, а оси x,y – как показано на
рис.16,б. Перенос системы координат
на второй стержень, где ось должна совпадать с осью стержня, осуществляется
поворотом системы координат вокруг оси y. Используя метод
сечений и принятые ранее правила построения эпюр, строим эпюры изгибающих
моментов ![]() (рис.17, а,б) и крутящих моментов
(рис.17, а,б) и крутящих моментов ![]() (рис.18). Пренебрегая влиянием продольных и
поперечных сил, определим опасное сечение для данной системы. Наиболее
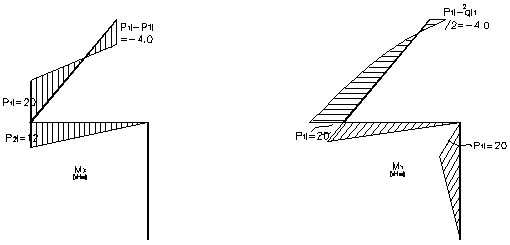
нагруженными являются сечения I-I и II-II (рис.17, а, б).
Определим, какое из них является наиболее опасным. Приведенный момент
(рис.18). Пренебрегая влиянием продольных и
поперечных сил, определим опасное сечение для данной системы. Наиболее
нагруженными являются сечения I-I и II-II (рис.17, а, б).
Определим, какое из них является наиболее опасным. Приведенный момент ![]() по
критерию Мизеса определяется по формуле
по
критерию Мизеса определяется по формуле
![]()
В сечении I-I
![]()
Видно, что сечение I-I является опасным и для него проводится расчет на прочность в опасной точке
![]()
Диаметр сечения d рамы будет равен
![]()
а)
б)
Рис. 17
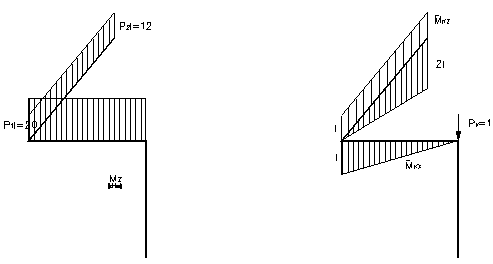
Рис. 18 Рис.
19
Округляя, принимаем d=25 мм. Для определения вертикального
перемещения точки к прикладываем в
этой точке единичную силу и строим эпюры единичных моментов ![]() (рис.19). Вертикальное перемещение точки
(рис.19). Вертикальное перемещение точки ![]() вычисляется по формуле:
вычисляется по формуле:
![]()
![]()
![]()
Учитываем, что
![]()
Пример 7.
Коленчатый стальной стержень прямоугольного поперечного сечения защемлен одним концом и нагружен поперечной силой P=0,9 кН на свободном конце. Определить в точках A и B защемленного сечения расчетные напряжения по третьей теории прочности (рис. 20).
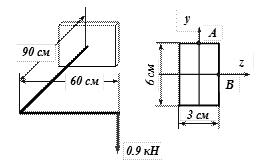
Рис.
20
Решение.
Построим эпюру моментов с целью определения величин внутренних силовых факторов, действующих в поперечном сечении стержня в заделке (рис.21).
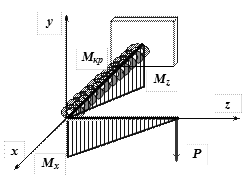
Рис.21
В результате действия силы P в защемленном сечении будут действовать изгибающий и крутящий моменты.
![]()
![]()
Эквивалентные напряжения по третьей теории прочности рассчитываются по формуле
![]()
Для точки B:
![]()
![]()
здесь ![]()
![]()
Для точки A:
![]()
![]()
![]()
![]()
Пример 8.
Для заданного ломаного бруса (рис. 22),
имеющего круглые поперечные сечения в пределах элементов длиной ![]() и
и ![]() , прямоугольное сечение в пределах элемента
длиной
, прямоугольное сечение в пределах элемента
длиной ![]() , требуется выполнить следующие расчеты:
, требуется выполнить следующие расчеты:
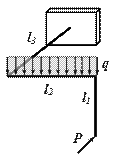
Рис.22
1. Построить эпюры продольных усилий, изгибающих и крутящих моментов,
2. Определить допускаемые нагрузки P и q, исходя из заданных размеров прямоугольного сечения элемента
бруса длиной ![]() ,
,
3. Определить диаметры круглых сечений
элементов бруса длиной ![]() и
и ![]() .
.
Примечания:
а) Построение эпюр внутренних силовых факторов производить, используя скользящую систему координат с постоянным направлением осей.
б) В расчетах на прочность использовать теорию максимальных касательных напряжений.
в) Прямоугольное сечение бруса длиной ![]() считать ориентированным так, что плоскость
наибольшей жесткости совпадает с плоскостью действия максимального изгибающего
момента.
считать ориентированным так, что плоскость
наибольшей жесткости совпадает с плоскостью действия максимального изгибающего
момента.
Дано:
![]()
![]()
Решение.
1. Построение эпюр внутренних силовых факторов
Для определения величины и характера
распределения внутренних силовых факторов по длине каждого участка ломаного бруса
построим эпюры продольных сил N, изгибающих ![]() и
крутящих
и
крутящих ![]() моментов. Поперечными силами Q в расчетах, как правило, пренебрегают,
так как их влияние незначительно. Для ломаного бруса, показанного на рис. 22,
эпюры внутренних силовых факторов приведены на рис. 23.
моментов. Поперечными силами Q в расчетах, как правило, пренебрегают,
так как их влияние незначительно. Для ломаного бруса, показанного на рис. 22,
эпюры внутренних силовых факторов приведены на рис. 23.
2. Определение допускаемой нагрузки P и q.
2.1 Определение опасного сечения элемента
бруса длиной ![]() .
.
Анализ эпюр показывает, что наиболее опасным
является сечение в заделке. В этом сечении действуют: максимальный изгибающий
момент ![]() , изгибающий момент
, изгибающий момент ![]() , постоянный по длине участка, крутящий
момент
, постоянный по длине участка, крутящий
момент ![]() , а также продольная сжимающая сила N.
, а также продольная сжимающая сила N.
2.2 Определение опасных точек в опасном сечении элемента
Прямоугольное сечение элемента бруса длиной ![]() ориентируем так, чтобы плоскость наибольшей
жесткости совпадала с плоскостью действия максимального изгибающего момента
ориентируем так, чтобы плоскость наибольшей
жесткости совпадала с плоскостью действия максимального изгибающего момента ![]() . Положение плоскости наибольшей жесткости
определяется жесткостью поперечного сечения относительно главных центральных
осей x и y, в частности, величиной максимального момента сопротивления. В
данном случае (рис. 24)
. Положение плоскости наибольшей жесткости
определяется жесткостью поперечного сечения относительно главных центральных
осей x и y, в частности, величиной максимального момента сопротивления. В
данном случае (рис. 24)
![]()
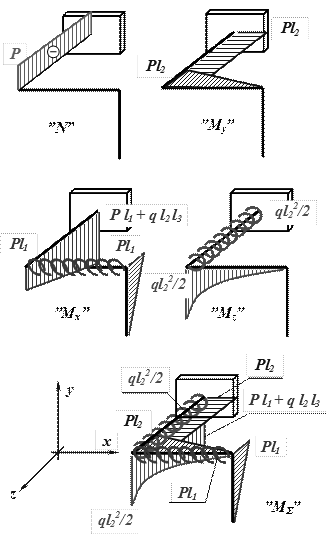
Рис.23
Максимальный изгибающий момент также
действует относительно оси x (![]() ). Следовательно, сечение должно быть
расположено так, как показано на рис. 24.
). Следовательно, сечение должно быть
расположено так, как показано на рис. 24.
Для определения положения опасных точек в
опасном сечении построим эпюры распределения нормальных (от ![]() ) и касательных (от
) и касательных (от ![]() ) напряжений (рис. 24).
) напряжений (рис. 24).
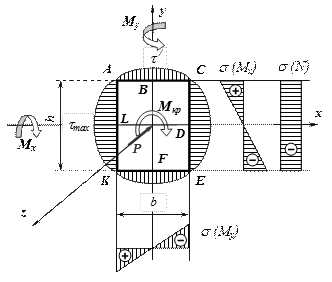
Рис.24
Эпюры нормальных и касательных напряжений показывают, что наиболее опасными являются следующие три точки этого сечения:
- точка E, где суммируются нормальные напряжения от ![]() , касательные
напряжения равны нулю,
, касательные
напряжения равны нулю,
- точка D, где суммируются нормальные напряжения от ![]() , а касательные напряжения от
, а касательные напряжения от ![]() принимают максимальные значения,
принимают максимальные значения,
- точка F, где суммируются нормальные напряжения от
![]() , а касательные
напряжения равны
, а касательные
напряжения равны ![]() .
.
2.3. Определение величин изгибающих и крутящих моментов в опасном сечении и моментов сопротивления.
Выразим q через
величину P. Так как по условию
задачи ![]() , то получаем
, то получаем
![]()
Моменты в опасном сечении имеют следующие значения:
![]()
![]()
![]()
При заданном соотношении h/b=2,5 и b=3 см моменты сопротивления принимают следующие значения:
![]()
![]()
![]()
где при h/b=2,5, ![]()
2.4 Определение допускаемой нагрузки
Расчет в точке E. В точке E имеют место только нормальные напряжения, поэтому на основании принципа независимости действия сил
![]()
![]()
![]()
Расчет в точке D. Для точки D имеем
![]()
![]()
![]()
Так как в точке D имеют место нормальные и касательные напряжения, используем условие прочности по третьей гипотезе
![]()
![]()
![]()
Расчет в точке F. Для точки F имеем
![]()
![]()
![]()
![]()
По III гипотезе прочности имеем
![]()
![]()
Из полученных результатов видно, что сосредоточенная сила P должна быть меньше или равна 3.3 кН, т.е. точка E оказалась самой опасной из трех.
3. Определение диаметров круглых сечений
элементов ломаного бруса при ![]()
3.1. Определение диаметра круглого сечения
элемента бруса длиной ![]() .
.
Опасным является сечение в конце участка,
если двигаться от свободного конца бруса, где действует один силовой фактор –
изгибающий момент ![]() . Условие прочности будет иметь вид
. Условие прочности будет иметь вид
![]()
![]()
![]()
3.2. Определение диаметра круглого сечения
элемента бруса длиной ![]() .
.
Анализ эпюр (рис.23) на втором участке
показывает, что опасным является сечение в конце участка, если двигаться со
свободного конца бруса, где изгибающие моменты ![]() и
и ![]() принимают максимальные значения, а крутящий
момент
принимают максимальные значения, а крутящий
момент ![]() , т.е. имеет место изгиб с кручением бруса
круглого поперечного сечения. На рис. 25 два изгибающих момента приведены к
одному суммарному и показаны опасные точки сечения A и B.
, т.е. имеет место изгиб с кручением бруса
круглого поперечного сечения. На рис. 25 два изгибающих момента приведены к
одному суммарному и показаны опасные точки сечения A и B.
Величины моментов
![]()
![]()
![]()
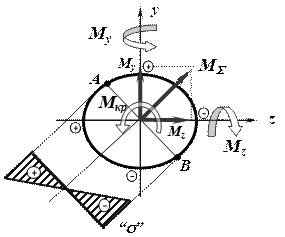
Рис.
25
Условие прочности для круглого сечения согласно III теории прочности имеет вид
![]()
где ![]()
![]()
![]()
![]()
Расчет пространственных ферм
Кинематический анализ пространственной фермы проводится по формуле
![]()
где nУ – число узлов фермы.
Требование W![]() 0 является
необходимым условием геометрической неизменяемости фермы. Для статической
определимости необходимо выполнение условия W=0.
Но, как известно, только количественного анализа еще недостаточно, следует
проводить и качественный анализ. Для этого можно использовать принципы
образования геометрически неизменяемых пространственных систем. Например,
простейшим принципом является присоединение к телу триады (шарового шарнира с
тремя связями). При его использовании вначале в ферме выделяют простейшее геометрически
неизменяемое тело – треугольную пирамиду. Затем к нему последовательно
присоединяют отдельные триады.
0 является
необходимым условием геометрической неизменяемости фермы. Для статической
определимости необходимо выполнение условия W=0.
Но, как известно, только количественного анализа еще недостаточно, следует
проводить и качественный анализ. Для этого можно использовать принципы
образования геометрически неизменяемых пространственных систем. Например,
простейшим принципом является присоединение к телу триады (шарового шарнира с
тремя связями). При его использовании вначале в ферме выделяют простейшее геометрически
неизменяемое тело – треугольную пирамиду. Затем к нему последовательно
присоединяют отдельные триады.
Геометрическую неизменяемость пространственной системы можно проверять и методом нулевой нагрузки: если при расчете системы без нагрузки усилия во всех стержнях и опорные реакции окажутся равными нулю, то система неизменяема, если же возникает неопределенность типа 0/0, система мгновенно изменяема.
Изучим два метода расчета пространственных ферм.
Метод сечений применяется при расчете ферм с простейшим образованием. Имеется два его варианта.
а) Метод вырезания узлов. Основан на последовательном вырезании узлов фермы, в которых
число неизвестных усилий не более трех. Составляются три уравнения проекций ![]() на три оси. Эти оси не должны быть
параллельными одной плоскости.
на три оси. Эти оси не должны быть
параллельными одной плоскости.
На этом методе
основан признак определения нулевых стержней (стержней, усилия в которых равны
нулю): если узел с тремя пересекающимися
стержнями не нагружен, то усилия во всех трех стержнях равны нулю.
б) Метод моментной оси. Сущность метода: через ферму проводится сквозное сечение, затем составляется и решается уравнение момента относительно некоторой оси.
Ось, для которой составляется уравнение момента, называется моментной осью. Эта ось выбирается так, чтобы в уравнение вошла только одна неизвестная.
Метод
разложения на плоские фермы. Когда стержни фермы располагаются группами
на нескольких плоскостях, этот метод дает большой выигрыш в расчетах. Метод
основан на следующей теореме: если силы,
действующие на пространственную ферму, лежат в одной плоскости, то усилия во
всех стержнях фермы, лежащих вне этой плоскости, равны нулю.
Порядок расчета фермы по этому методу состоит в следующем: внешняя нагрузка разлагается на несколько плоскостей; части фермы, лежащие в разных плоскостях, рассчитываются только на нагрузку в своей плоскости; затем применяется принцип суперпозиции.
Например, на следующую ферму (рис. 26,а) нагрузка действует только в двух плоскостях. Следовательно, ее расчет можно свести к расчету только двух плоских ферм (рис. 26,б, в). В стержнях фермы, лежащих на третьей плоскости (рис. 26,г), все усилия равны нулю.
Рис.
26
Вопросы для самопроверки
- Какую раму называют плоско-пространственной?
- Какие внутренние силовые факторы возникают в поперечных сечениях указанной рамы?
- Какую раму называют пространственной?
- Какие внутренние силовые факторы возникают в поперечном сечении пространственной рамы?
- Как в пространственных рамах при построении эпюры внутреннего силового фактора ориентируют ее плоскость?
Задачи для самостоятельного решения
Задача
1.
Для пространственных стержней, представленных на рис. 27 и рис.28, требуется построить эпюры крутящих и изгибающих моментов, поперечных сил.
Опорами пространственных брусьев являются подшипники, которые препятствуют линейным перемещениям в направлении двух осей z и у.
Задача 2.
Подобрать по III теории прочности (по критерию
наибольших касательных напряжений) размеры сплошного прямоугольного поперечного
сечения ![]() пространственного стального бруса,
изображенного на рис. 28 предыдущего примера. Брус состоит из прямолинейных
участков, перпендикулярных друг другу, a =
0,2 м.
пространственного стального бруса,
изображенного на рис. 28 предыдущего примера. Брус состоит из прямолинейных
участков, перпендикулярных друг другу, a =
0,2 м.
Размеры поперечного сечения бруса определять при условии, что отношение сторон k = h/b = 2 задано, а q = 5 кН/м, Radm = Ry = 240 МПа.
Ответ: b(3) = 1,5 см; h = 3 см.
Задача 3.
Определить внутренние усилия и перемещения на участке AB консольного пространственного бруса ABCD круглого сечения (рис.29) диаметром d, нагруженного горизонтальной силой P. Модуль Юнга равен E, геометрические размеры: AB=l, BC=CD=l/2.
Рис.29
Задача 4.
Определить внутренние усилия и перемещения на участке AB консольного пространственного бруса ABCD круглого сечения (рис.30) диаметром d, нагруженного горизонтальной силой P. Модуль Юнга равен E, геометрические размеры: AB=l, BC=CD=l/2.
Рис.30
Задача 5.
Определить внутренние усилия и перемещения на участке AB консольного пространственного бруса ABCD круглого сечения (рис.31) диаметром d, нагруженного вертикальной силой P. Модуль Юнга равен E, геометрические размеры: AB=l, BC=CD=l/2.
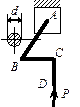
Рис.31
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов