Главная
Лекция
12. Определение перемещений в упругих
системах.
Общие теоремы об упругих системах
Содержание
Потенциальная
энергия деформации стержня в общем случае его нагружения
Обобщённые
силы и обобщенные перемещения
Работа
внешних сил. Теорема Клапейрона
Теоремы
о взаимности работ и взаимности перемещений
Теорема
Кастильяно. Теорема Лагранжа
Теорема
о минимуме потенциальной энергии
Любая конструкция под действием приложенных внешних нагрузок изменяет в той или иной степени свою форму и размеры – деформируется. Для проверки жесткости и устойчивости конструкции необходимо уметь определять перемещения, вызванные деформацией ее элементов. Кроме того, определение перемещений конструкции является важнейшей вспомогательной задачей при расчете статически неопределимых систем.
Перемещение
– векторная величина. Перемещение любой точки на плоскости можно задать через
его модуль и направление. Например, вектор перемещения 
точки А рамы в точку А¢ (рис. 12.1,а)
определяется через его модуль 
и угол (направление) 
(рис. 12.1,б).
А эти величины можно определять через горизонтальную и вертикальную
составляющие 
и 
вектора перемещения 
:
Поступательные
перемещения 
будем называть линейными перемещениями,
а – угловым перемещением.
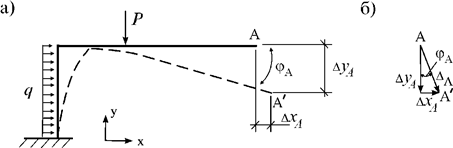
Рис. 12.1
Методы определения этих перемещений весьма разнообразны. Они отличаются друг от друга главным образом степенью сложности и областью применения.
Исторически первым предложенным методом определения перемещений можно считать метод непосредственного интегрирования дифференциального уравнения упругой линии балки. Однако в случае балок с большим количеством участков реализация этого метода сопряжена со значительными трудностями, которые заключаются не в интегрировании дифференциальных уравнений, а в технике определения произвольных постоянных интегрирования – составлении и решении систем линейных алгебраических уравнений.
Если по условиям нагружения балка разбивается на n участков, то задача становится очень трудоемкой уже при n=3. Для уменьшения большого объема вычислительной работы, связанной с определением произвольных постоянных интегрирования, разработан ряд методов, из которых, прежде всего, отметим метод начальных параметров, позволяющий при любом числе участков свести решение к отысканию только двух постоянных – прогиба и угла поворота в начале координат.
Указанные методы, как и некоторые другие, носят частный характер. С некоторой натяжкой их можно признать удобными при решении ограниченного круга простейших задач.
Кроме аналитических методов вычисления прогибов и углов поворота сечений балок существуют более общие методы, пригодные для определения перемещений в любых упругих конструкциях (например, метод Мора, иногда говорят Максвелла-Мора. Эти методы основаны на двух основных принципах механики: законе сохранения энергии и начале возможных перемещений.
Прежде чем перейти к изложению метода, остановимся на его основных теоретических предпосылках.
Потенциальная энергия деформации стержня в общем случае его нагружения
При статическом растяжении или сжатии упругого стержня происходит превращение потенциальной энергии из одного вида в другой. Потенциальной будем называть такой вид энергии, который накапливается в теле при его упругих деформациях. При нагружении стержня внешними силами часть потенциальной энергии действующего на стержень груза полностью переходит в потенциальную энергию деформации стержня. Действительно, если мы будем нагружать стержень с помощью малых грузов dP (рис.12.1.1), то при добавлении каждого такого груза подвешенная уже часть нагрузки будет опускаться и ее потенциальная энергия будет уменьшаться, а потенциальная энергия деформации стержня соответственно увеличиваться.
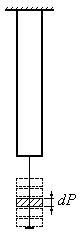
Рис.12.1.1
Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке. Такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.
Будем называть “статической” такую нагрузку, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения этих частей, т.е. скорость остается постоянной и ускорение отсутствует.
При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой. При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере.
Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу. Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.
Таким образом, можно сказать, что полное
преобразование одного вида потенциальной энергии в другой имеет место, если
деформация происходит без нарушения равновесия системы. Мерой
энергии, превратившийся в другой вид, является величина работы, произведенной
силами, действующими на конструкцию.
Обозначим величину накопленной потенциальной энергии деформаций через U, а уменьшение потенциальной энергии внешних нагрузок через Up. Тогда величина Up измеряется положительной работой этих нагрузок Ap; с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, межчастичных сил W, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.
Закон сохранения энергии при деформациях упругих систем принимает вид:
Заменяя в этой формуле величины Up и U численно равными им значениями работ Ap и -W, получаем иную формулировку этого закона:
Эта формулировка закона сохранения энергии совпадает с
так называемым “началом” или “принципом” возможных перемещений в применении к
упругим системам. Равенство (2) выражает ту мысль, что при перемещениях без
нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна
нулю.
Таким образом, принцип возможных перемещений в применении к упругим системам является следствием закона сохранения энергии.
Из формулы (1) следует, что потенциальная энергия деформации U численно равна работе внешних сил Ap, проделанной ими при этой деформации:
Обобщённые силы и обобщенные перемещения
Прежде, чем перейти к вычислению работы внешних сил, а
через нее к потенциальной энергии деформации, введем понятие обобщенной силы и обобщенной координаты.
В задачах сопротивления материалов и строительной механики внешняя нагрузка отличается большим разнообразием и обычно представляет собой группы сил. Выражение для работы группы постоянных сил можно представить в виде произведения двух величин:
в котором множитель P зависит только от сил группы и называется обобщенной
силой, а 
зависит от перемещений
и называется обобщенным перемещением или обобщенной координатой.
Таким образом, под обобщенной силой следует понимать
любую нагрузку (сосредоточенные силы, сосредоточенные пары, распределенную
нагрузку), вызывающую соответствующее нагрузке перемещение. Обобщенной
координатой будем называть перемещение, соответствующее этой силе.
“Соответствие” заключается в том, что речь идет о перемещении того сечения, где приложена рассматриваемая сила, причем о таком перемещении, что произведение его на эту силу дает нам величину работы. Для сосредоточенной силы это будет линейное перемещение по направлению действия силы – прогиб, удлинение, для пары сил – это угол поворота сечения по направлению действия пары.
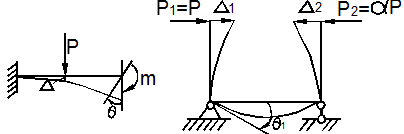
На рис.12.2, б,в,г обобщёнными силами будут две силы Р, два момента m, распределённая нагрузка q.
а)
б)
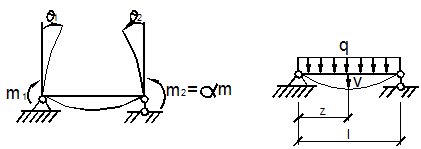
в)
г)
Рис. 12.2
Производимая ими работа соответственно равна:
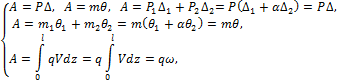
где 
а величина 
представляет собой площадь между исходной и
изогнутой осями балки.
Обобщёнными силами могут быть не только внешние, но и внутренние: 
.
Рассмотрим например статически неопределимую балку (рис. 12.3).
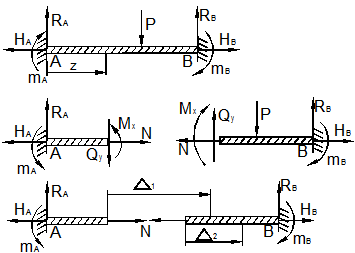
Рис. 12.3
Рассечём
её на расстоянии z от левого конца и приложим к краям
разреза по две нормальные силы N, две перерезывающие 
,
два изгибающих момента 
,
каждая из которых образует группу сил, характеризуемых одним числом, т.е. обобщённую силу.
Возьмём две нормальные силы N. Они совершат работу:
Обобщённое
перемещение 
представляет собой относительное расхождение
краёв разреза. Аналогично можно рассмотреть две силы и два момента .
Обобщенные
перемещения принято обозначать буквами 
или 
с двумя индексами. Первый индекс обозначает
точку и направление перемещения, а второй указывает причину, вызвавшую искомое
перемещение. Например, 
обозначает перемещение точки приложения силы F по направлению ее
действия, вызванное этой же силой.
Для
обозначения полного перемещения точки, вызванного несколькими обобщенными
силами, при сохраняется только первый индекс.
Перемещение,
вызванное безразмерной единичной силой 
или безразмерной единичной парой 
,
обозначается символом и называется удельным.
Работа внешних сил. Теорема Клапейрона
Вычислим работу некоторой обобщенной силы P,
приложенной к любой упругой линейно деформируемой системе (рис.12.4,а). Предполагается, что нагрузка
возрастает от нуля до заданной величины достаточно медленно, чтобы при этом
можно было пренебречь силами инерции перемещаемых масс.
Пусть в данный момент силе P
соответствует обобщенное перемещение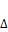 
.
Бесконечно малое приращение силы на величину dP
вызовет бесконечно малое приращение перемещения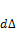 
.
Элементарная работа внешней силы, если пренебречь бесконечно малыми второго
порядка, равна:
Полная работа, совершенная статически приложенной обобщенной силой P, вызвавшей обобщенное перемещение ∆, имеет вид:
Интеграл
(5) представляет собой площадь диаграммы 
для данной конструкции (рис.12.4,б).
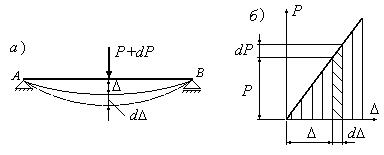
Рис.12.4
В линейно деформируемых системах перемещения пропорциональны величине силы (закон Гука):
где 
-
перемещение, вызванное силой 
Дифференцируем выражение (6):
Подставляя полученное выражение в формулу (5), найдем:
Учитывая выражение (6), окончательно получим:
Полученное выражение известно под названием теоремы Клапейрона: действительная работа при статическом действии силы на упругую систему равна половине произведения окончательного значения силы на окончательное значение соответствующего ей обобщенного перемещения.
В
случае статического действия на упругую систему нескольких обобщенных сил 
работа деформации равна половине суммы
произведения окончательного значения каждой силы на окончательное значение
соответствующего обобщенного перемещения:
Вычисление потенциальной энергии деформации. Определение перемещений при непосредственном использовании потенциальной энергии
Из выражения (3) следует, что потенциальная энергия
деформации численно равняется работе внешних сил на вызванных ими перемещениях
и, следовательно, может быть вычислена с учетом теоремы Клапейрона
из выражения:
где P - обобщенная сила; - соответствующая ей обобщенная координата.
Вычислим потенциальную энергию для некоторых видов
деформации, используя выражение (9).
При статическом растяжении и сжатии стержня силами P величина работы 
, а, следовательно, и величина потенциальной энергии U равняется:
Здесь: N - продольная сила; 
- абсолютное удлинение стержня; E - модуль
упругости первого рода; A - площадь поперечного сечения стержня; l - длина стержня.
В случае сдвига
Здесь: Q - поперечная сила; a - размер поперечного сечения; 
- величина абсолютного сдвига; G - модуль упругости второго рода, модуль сдвига; A - площадь поперечного сечения.
При кручении
Здесь: 
- крутящий момент; 
- угол закручивания; 
- полярный момент инерции; l - длина скручиваемого стержня.
При чистом изгибе концевые сечения балки (рис.12.5)
под действием изгибающих моментов повернутся на угол 
, где - центральный угол изогнувшейся по дуге радиусом 
оси балки.
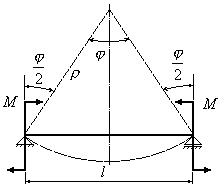
Рис.12.5
Тогда
При плоском поперечном изгибе работу на вызванных внешними силами перемещениях совершает также и поперечная сила Q. Вычислим эту работу.
Как
отмечалось ранее, поперечные силы являются равнодействующими распределенных в
точках сечения касательных напряжений 
(рис.12.6,а).
Последние в любой элементарной площадке 
,
параллельной нейтральной линии сечения (рис.12.6,б), согласно формуле Д.И.Журавского
таковы:
где 
-
статический момент площади отсеченной части сечения относительно нейтральной
линии Oz.
На
основании закона Гука взаимный сдвиг двух соответствующих площадок dA, взятых на торцах mn
и 
(рис.12.6,в),
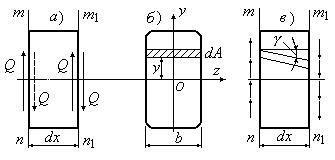
Рис.12.6
Следовательно,
работа внутренних элементарных сил 
при их нарастании от нуля до окончательного
значения
Интегрируя
в пределах сечения 
, получим работу поперечных сил:
где 
-
коэффициент, зависящий от формы поперечного сечения; GA -
жесткость поперечного сечения стержня при сдвиге.
Для прямоугольного сечения k=1,2; для кругового - k=32/27; для прокатных профилей
приближенно 
, где 
- площадь стенки.
В случае чистого сдвига касательные напряжения распределяются равномерно по сечению:
Следовательно
Полученное выражение с точностью до знака совпадает с
выражением для потенциальной энергии при чистом сдвиге (11).
Используя численное равенство потенциальной энергии деформации абсолютной величине работы внутренних сил, можно записать величину элементарной работы при осевом растяжении и сжатии:
при кручении:
при плоском поперечном изгибе
Складывая полученные значения для
элементарной работы внутренних сил и интегрируя по длине стержня, можно
получить полную работу внутренних сил для общего случая действия сил на
стержень при возникновении всех шести силовых факторов:
Потенциальная энергия при возникновении всех шести
внутренних силовых факторов с учетом 
принимает вид:
Из приведенной формулы видно, что потенциальная
энергия деформации является квадратичной функцией обобщенных сил или обобщенных
перемещений, так как последние линейно связаны с обобщенными силами.
Следовательно, потенциальная энергия деформации всегда положительна. Ее
величина не зависит от порядка нагружения и целиком определяется окончательными
значениями усилий и перемещений. Отметим также, что потенциальная энергия как
квадратичная функция обобщенных нагрузок не подчиняется принципу независимости
действия сил. Это значит, что потенциальная энергия, накопленная в результате
действия группы сил, не равна сумме потенциальных энергий, вызванных действием
каждой нагрузки в отдельности. Закон независимости действия сил при вычислении
потенциальной энергии применим лишь в тех случаях, когда перемещение по
направлению одной обобщенной силы, вызванное действием другой силы, равно нулю.
Приведенные выражения для потенциальной энергии
деформации получены для статического приложения нагрузок при сохранении
равновесия в течение всего процесса нагружения. Следует сказать, что полученные
формулы сохраняют силу и при любом способе приложения нагрузок, лишь бы
значения сил и деформаций были связаны линейной зависимостью и относились к
тому моменту, когда установится равновесие конструкции.
Рассмотрим несколько примеров определения перемещений
с применением потенциальной энергии деформации.
Пример 1.
Определить величину потенциальной энергии деформации в
шарнирно-стержневой системе (рис.12.7), нагруженной в узле В
вертикальной силой P=40кН. Стержни АВ и ВС имеют одинаковые площади
поперечного сечения A=5см2 и изготовлены из одного материала 
МПа. Найти (в мм) вертикальное перемещение узла В.
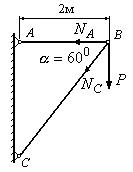
Рис.12.7
Решение.
1. Находим усилия в стержнях АВ и ВС:
Из уравнения (б) находим: 
кН; из
уравнения (а) находим : 
кН.
2. Определяем потенциальную энергию системы:
3.
Находим вертикальное перемещение узла В. Представим потенциальную энергию
деформации как половину произведения силы P, приложенной в узле, на
вертикальное перемещение узла В 
:
Откуда:
Пример
2.
Вычислить потенциальную энергию деформации балки на двух опорах (рис.12.8), нагруженную силой P=30 кН. Определить перемещение под силой и посредине пролета. Жесткость поперечного сечения балки принять равной EJ=3600 кНм2.
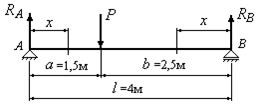
Рис.12.8
Решение.
1. Вычисляем опорные реакции:
2. Вычисляем изгибающий момент на каждом участке:
3. Определяем потенциальную энергию деформации:
4.
Находим прогиб под силой. Для этого вычислим работу, которую совершает сила P на перемещении балки 
:
откуда
5. Находим прогиб посредине балки при a=b=l/2. Получим:
Теоремы о взаимности работ и взаимности перемещений
Установим зависимость между деформациями в различных
сечениях балки, пользуясь понятием потенциальной энергии.
Если к балке, нагруженной силой 
в сечении №1
(рис.12.9), приложить затем статически силу 
в сечении №2,
то к прогибу точки приложения силы от этой же силы
прибавится
прогиб от силы , равный 
. Порядок индексации у перемещений описан выше.
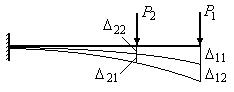
Рис.12.9
Полная работа внешних сил будет
состоять из трех частей: работы силы на вызванном ею перемещении , т.е. 
; работы силы на вызванном ею перемещении 
, т.е. 
; работы силы на перемещение точки ее приложения от силы , т.е. 
.
Таким образом, накопленная в балке при действии обеих сил
энергия будет равна:
Как отмечалось выше, количество энергии деформации
зависит лишь от конечных значений сил и прогибов и не зависит от порядка
нагружения.
Если теперь к балке, нагруженной силой , приложить силу , то повторив цепь вычислений, получим:
Сравнивая оба значения потенциальной энергии U, имеем:
Выражение (23) представляет собой теорему о взаимности работ,
была выведена итальянским ученым Энрико Бетти и
формулируется следующим образом: работа
силы 
(или первой группы сил) на перемещениях,
вызванных силой 
(второй группой сил), равна работе силы на перемещениях, вызванных силой .
Эта теорема имеет важное практическое применение. Если
, то 
. Пользуясь этим свойством взаимности, можно упростить
выполнение опытов по определению перемещений. Пусть мы хотим экспериментальным
путем найти прогибы в сечениях №1, №2, №3, №4 балки, защемленной одним концом А и нагруженной на другом конце В силой P (рис.12.10).
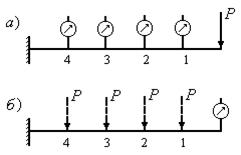
Рис.12.10
Вместо того, чтобы ставить
для каждой точки свой прибор для измерения перемещений (прогибомер)
(рис.12.10,а) или переносить прибор,
что всегда неудобно и может привести к ошибкам измерения, можно поступить
иначе. Поставим прогибомер в точке
В, а силу P будем последовательно прикладывать в сечениях №1, №2,
№3, №4 (рис.12.10,б). Измеренные в
точке В прогибы и будут по теореме Бетти равны
прогибам точек №1, №2, №3, №4 от силы P, приложенной в точке В.
Применяя теорему Бетти к частному случаю нагружения,
когда в обоих состояниях приложено по одной обобщенной силе 
и 
в точках №1 и
№2 (рис.12.9). На основании формулы (23)
а так как 
, то
Выражение (24) носит название теоремы о взаимности перемещений
(теоремы Джеймса Клерка Максвелла) и формулируется следующим образом: перемещение точки приложения первой
единичной силы по ее направлению, вызванное действием второй единичной силы,
равно перемещению точки приложения второй единичной силы по ее направлению,
вызванному действием первой единичной силы.
Теоремы о взаимности работ и перемещений имеют большое
значение в общей теории исследования напряженного и деформированного состояния
стержней, пластинок, оболочек и других конструкций. Их применение существенно
упрощает решение многих задач строительной механики, а также,
как уже отмечалось выше, производство опытов по определению перемещений.
Пример
3.
Пусть требуется найти прогиб точки В посередине пролёта балки от действия момента m в опоре А (рис. 12.11).
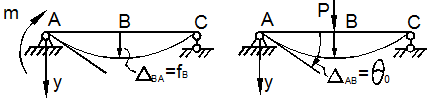
а)
б)
Рис. 12.11
Решение.
Для
определения перемещения 
(рис. 12.11, а) воспользуемся теоремой о взаимности работ. Рассмотрим такую же
балку, нагруженную в точке В силой Р (рис. 12.9, б). Решение этой задачи нам известно:
На основании теоремы о взаимности работ
откуда прогиб
Теорема Кастильяно. Теорема Лагранжа
Пусть упругая система статически нагружена
произвольной нагрузкой Q и некоторой обобщенной силой P (рис.12.12). Вычислим потенциальную энергию,
накопленную при деформации системы. С этой целью для удобства примем следующий
порядок нагружения. Вначале нагружаем систему силой P. Перемещение точки приложения силы по ее направлению
и от ее действия обозначим 
. Затем прикладываем нагрузку Q.
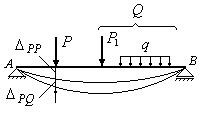
Рис.12.12
В результате
дополнительной деформации сила P получит перемещение 
. Полное (обобщенное) перемещение точки приложения
силы
Потенциальная энергия деформации, накопленная в
системе, будет численно равна работе внешних сил:
где 
- энергия, накопленная в результате деформирования
системы только силами Q, численно равная работе сил Q на вызванных ими перемещениях.
Второй член в формуле (26) не содержит 1/2, так как на
перемещении , сила P, выполняя работу, не изменяла своего значения. Так
как 
, то формулу (26) можно записать в виде:
Продифференцируем выражение (27) по силе P с учетом равенства (25):
Таким образом,
Перемещение точки приложения обобщенной силы по
направлению ее действия равно частной производной от потенциальной энергии по
этой силе.
Эта теорема носит имя итальянского механика и инженера
Карло Альберто Кастильяно и является одной из
основных в строительной механике; выведенная первоначально для шарнирных ферм,
она была обобщена автором на упругое тело любого вида. В связи с широким
внедрением в расчетную практику метода Мора способ Кастильяно
был вытеснен из практики определения перемещений в стержневых системах. Однако
он остается общим методом определения перемещений в нестержневых
системах (пластинках, оболочках и деталях, все три измерения которых имеют один
порядок).
Приведём пример применения теоремы Кастилиано. Потенциальная энергия упругой однопролётной балки длиной l с шарнирным закреплением краёв и сосредоточенной поперечной силой посередине пролёта равна:
По формуле (28) находим:
Заметим, что согласно формуле (28) вторая производная
от потенциальной энергии по обобщенной силе равняется
Учитывая, что 
является строго
положительной величиной, вторая производная от потенциальной энергии по
обобщенной силе также является положительной величиной.
Для плоской системы, пренебрегая влиянием продольной и
поперечной сил, потенциальную энергию
запишем в виде:
Применяя правило дифференцирования по параметру,
находим:
Чтобы определить линейное или угловое перемещение в
сечении, где по условию задачи сила отсутствует, в этом сечении следует
приложить соответствующую фиктивную обобщенную силу. Далее, написав выражение
для потенциальной энергии от системы сил, включая указанную фиктивную силу,
следует взять ее производную по этой фиктивной силе и в полученном выражении
для перемещения приравнять фиктивную нагрузку нулю.
Выразив потенциальную энергию деформации в функции
независимых перемещений 
, можно показать, что частная производная от потенциальной
энергии по любому перемещению равна силе, действующей по направлению
перемещения, т.е.:
Сформулированная теорема была установлена французским
математиком и механиком Жозефом Луи Лагранжем и носит его имя.
Рассмотрим
теперь нелинейное упругое тело. Пусть потенциальная энергия деформации выражена
через перемещения 
.
Образуем функцию
называемую дополнительной работой или потенциальной энергией сил. Проварьируем её:
Так
как по теореме Лагранжа 
то получаем:
Предположим, что функция Ф выражена только через внешние силы:
тогда
Заменяя левую часть (32) полученным выражением, находим:
откуда
в силу произвольности 
получаем:
Эта
формула (33) выражает собой теорему Кастилиано для
нелинейно упругого тела: частная производная от дополнительной работы
по силе равна перемещению в направлении
этой силы.
Термин «дополнительная работа» легко понять из рис. 12.13, на котором заштрихованная область изображает работу внутренних сил, т.е. потенциальную энергию деформации.
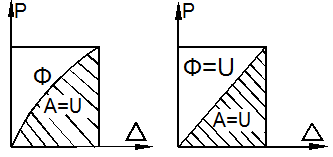
а)
б)
Рис. 12.13
Дополнительная работа Ф представляет собой площадь, дополняющую U до прямоугольника. Иногда её называют работой или энергией сил.
Рассмотрим несколько примеров применения теорем Кастильяно и Лагранжа.
Пример
4.
Используя теорему Кастильяно, определить прогиб и угол поворота в сечении В для балки, изображенной на рис.12.14, если жесткость поперечного сечения балки EJ=12000 кНм2.
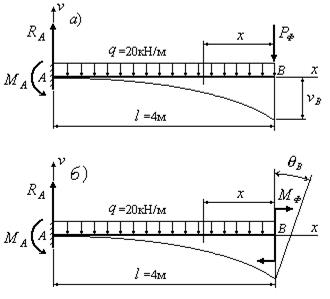
Рис.12.14
Решение.
1. Добавим в сечении В
сосредоточенную фиктивную силу и запишем выражение для изгибающего момента с
учетом этой силы:
2. Возьмем частную производную от изгибающего момента 
в выражении (а)
по фиктивной силе 
:
3. Подставим выражения (а) и (б) в формулу (30).
Учитывая, что 
, получим:
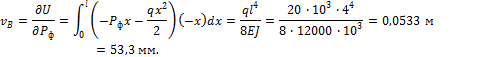
4. Для определения угла поворота в сечении В добавим в этом сечении фиктивный момент 
, запишем выражение для изгибающего момента в сечении x с учетом этого момента:
5. Возьмем частную производную по :
и подставим выражения (в) и (г) в формулу (30).
Учитывая, что 
, получим угол поворота в сечении В:
Пример 5.
Определить величину силы P, приложенной к статически неопределимой стержневой
система в точке В, если опускание узла В 
мм (рис.12.15).
Жесткость поперечного сечения одинакова
для всех стержней и равна EA=1200 Н. Угол наклона крайних стержней 
. Длина крайних стержней №1 и №2 
м. Длина
среднего стержня №3 с учетом наклона крайних стержней 
м.
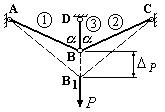
Рис.12.15
Решение.
1. Выразим деформации стержней фермы через перемещение
точки В 
:
2. Выразим усилия в стержнях фермы через перемещение
точки В:
3. Вычислим потенциальную энергию деформации, которая
накапливается в системе:
4. Возьмем частную производную от выражения
потенциальной энергии по :
Пример 6.
Приведём пример применения теоремы Лагранжа к нелинейной упругой системе.
Потенциальная энергия двух растягиваемых стержней (рис. 12.16):
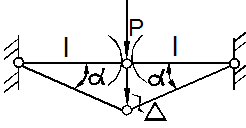
Рис. 12.16
В
силу закона Гука 
.
Из
рис. 12.16 следует перемещение 
Так
как 
то
Следовательно, потенциальная энергия:
может
быть выражена через перемещение .
Поскольку условия для использования формулы Лагранжа соблюдены, получаем:
Пример 7.
Одним из простых примеров применения теоремы Кастилиано к определению перемещений является расчёт винтовой пружины.
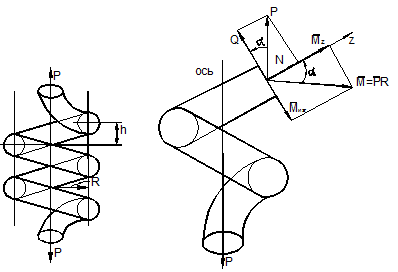
а)
б)
Рис. 12.17
Винтовая,
или витая, пружина – это пространственно изогнутый
стержень (рис. 12.17, а). На рис.
12.17, б показана отсечённая часть
пружины с углом подъёма витка 
.
Приведём, направленную по оси пружины силу Р к центру тяжести сечения. В результате получим вектор-момент 
.
Разлагая его на направление касательной к винтовой линии Z и перпендикулярное направление,
найдём крутящий и изгибающие моменты:
Нормальной силой N, перерезывающей силой Q пренебрежём.
Так как моменты всюду постоянны, то на основании (20):
Перемещение точки приложения силы Р к пружине:
Наибольшее напряжение изгиба:
Наибольшее напряжение кручения:
На
практике обычно применяются пружины с малым углом подъёма .
Для таких пружин можно принять 
Тогда
Условие
прочности: 
Теорема о минимуме потенциальной энергии
Рассмотрим три раза статически неопределимую систему
(рис.12.18,а), усилия в элементах
которой определить только из уравнений равновесия нельзя. Превратим
систему в статически определимую, удалив соответствующее число связей. В
данном примере (рис.12.18,б)
отброшены три связи – шарнирно подвижные опоры В, С и D. Действие отброшенных связей заменим соответствующими
реакциями 
, которые будем рассматривать как независимые друг от
друга внешние нагрузки.
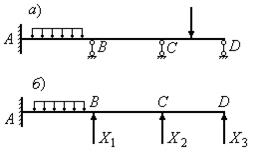
Рис.12.18
Вычислим с помощью метода Кастильяно
перемещения 
точек
приложения сил 
по направлению
их действия:
где 
- потенциальная энергия деформации системы.
Так как эти перемещения равны нулю, то
Уравнение (34) является необходимым условием
экстремума функции U. Легко видеть, что этот экстремум является минимумом,
так как согласно формуле (29) вторые производные функции U по равны:
Перемещения 
- существенно положительные
величины, а положительный знак вторых производных свидетельствует о том, что
условия задачи (34) являются условиями минимума функции U.
Таким образом, приходим к теореме о минимуме потенциальной энергии: в статически неопределимых системах лишние неизвестные усилия принимают
такие значения, при которых потенциальная энергия деформации имеет наименьшее
значение.
Эта теорема была установлена итальянским математиком,
механиком и военным инженером Луиджи Федериго Менабреа и носит его
имя. Теорема известна также как теорема о наименьшей работе, так как вместо
потенциальной энергии можно говорить о численно равной ей работе внешних сил.
На основании приведенной теоремы можно заключить, что
при добавлении каких-либо связей потенциальная энергия тела всегда уменьшается.
Вопросы для самопроверки
- Дайте определение перемещению точки?
- Что такое перемещения и какова символика их обозначения?
- Охарактеризуйте предпосылки, на которых построено определение перемещений в стержневых системах?
- Для чего нужно уметь определять перемещения?
- Какие перемещения определяются для балок при действии нагрузки?
- Какие эпюры внутренних усилий необходимо построить при определении перемещений в балке?
- По какой формуле определяются перемещения в балке при действии нагрузки?
- Что называют обобщенной силой и обобщенным перемещением?
- Что понимается под возможным (виртуальным) перемещением?
- Что понимается под обобщенной силой?
-
Расшифруйте запись: 
- Как определяется возможная работа внешних сил?
- Работа внешних и внутренних сил.
- Потенциальная энергия.
- Теорема о взаимности перемещений.
- Какая нагрузка называется статической?
- Как определяется действительная работа внешних сил?
- Как определяется виртуальная работа изгибающих моментов, поперечных и продольных сил?
- По какой формуле вычисляется действительная работа внутренних сил?
- Как определяется потенциальная энергия деформаций системы?
- Потенциальная энергия деформации. Понятие обобщенного перемещения. Теорема Лагранжа. Теорема Кастильяно.
- Сформулируйте теорему о взаимности возможных работ внешних сил. Какие теоремы взаимности строительной механики вытекают из этой теоремы?
- Сформулируйте теорему о взаимности перемещений и запишите её в математической форме.
- Сформулируйте теорему о взаимности реакций и запишите её в математической форме.
- Сформулируйте теорему о взаимности реакций и перемещений и запишите её в математической форме.
- Работа внутренних и внешних сил на обобщенных перемещениях. Теорема взаимности работ. Теорема взаимности перемещений.
- Получите выражение действительной работы внешних и внутренних сил?
- В чем отличие действительной работы от возможной?
- Как формулируется теорема о взаимности работ? Приведите доказательство этой теоремы?
- Как формулируется теорема о взаимности перемещений? Приведите доказательство этой теоремы?
- Что понимается под фиктивной нагрузкой при определении прогиба графоаналитическим методом?
- На чем основан энергетический метод определения перемещений балки?
- Сформулируйте теорему о взаимности работ?
- Сформулируйте теорему Кастильяно?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
