Главная

Лекция 13 (продолжение). Примеры решения на вычисление перемещений методом Мора-Верещагина

Определение перемещений в балках

Пример 1.

Определить перемещение точки К балки (см. рис.) при помощи интеграла Мора.

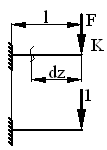
Решение.

1) Составляем уравнение изгибающего момента от внешней силы M_F.

2) Прикладываем в точке К единичную силу F = 1.

3) Записываем уравнение изгибающего момента от единичной силы .

4) Определяем перемещения

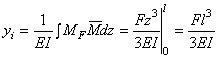
Пример 2.

Определить перемещение точки К балки по способу Верещагина.

Решение.

1) Строим грузовую эпюру.

2) Прикладываем в точке К единичную силу.

3) Строим единичную эпюру.

4) Определяем прогиб

; ;

Пример 3.

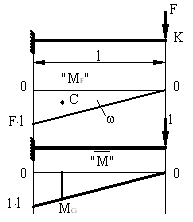
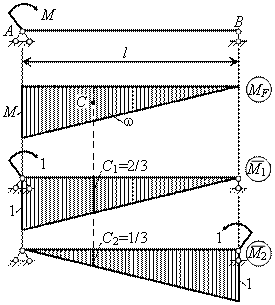
Определить углы поворота на опорах А и В для заданной балки (см. рис.).

Решение.

Строим эпюры от заданной нагрузки и от единичных моментов, приложенных в сечениях А и В (см. рис.). Искомые перемещения определяем с помощью интегралов Мора

,

, которые вычисляем по правилу Верещагина.

Находим параметры эпюр

C₁ = 2/3, C₂ = 1/3,

а затем и углы поворота на опорах А и В

Пример 4.

Определить угол поворота сечения С для заданной балки (см. рис.).

Решение.

Определяем опорные реакции R_A=R_B,

, , R_A = R_B = qa.

Строим эпюры изгибающего момента от заданной нагрузки и от единичного момента, приложенного в сечении С, где ищется угол поворота. Интеграл Мора вычисляем по правилу Верещагина. Находим параметры эпюр

C₂ = -C₁ = -1/4,

а по ним и искомое перемещение

.

Пример 5.

Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.

1. Построение эпюр изгибающих моментов.

Эпюра M_F (рис. б)

Опорные реакции:

ВЕ: , ,

, R_B + R_E = F, R_E = 0;

АВ: , R_А = R_В = F; , .

Вычисляем моменты в характерных точках , M_B = 0, M_C = Fa и строим эпюру изгибающего момента от заданной нагрузки.

Эпюра (рис. в).

В сечении С, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента, вычисляя сначала опорные реакции ВЕ - , , = 2/3; , , = 1/3, а затем моменты в характерных точках , , .

2. Определение искомого прогиба. Воспользуемся правилом Верещагина и вычислим предварительно параметры эпюр и :

,

Прогиб сечения С

.

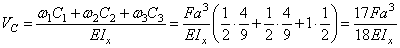Пример 6.

Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С. Пользуясь правилом Верещагина, вычисляем параметры эпюр ,

и находим искомый прогиб

.

Пример 7.

Определить прогиб в сечении С для заданной балки (см. рис.).

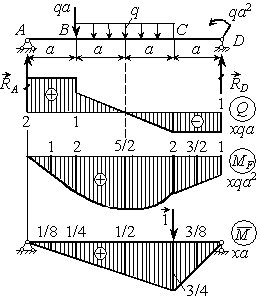
Решение.

1. Построение эпюр изгибающих моментов.

Опорные реакции:

, , R_A = 2qa,

, R_A + R_D = 3qa, R_D = qa.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С.

2. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка.

Участок АВ:

Участок ВС:

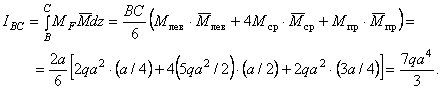
Участок СD:

Искомое перемещение

.

Пример 8.

Определить прогиб сечения А и угол поворота сечения Е для заданной балки (рис. а).

Решение.

1. Построение эпюр изгибающих моментов.

Эпюра М_F (рис. в). Определив опорные реакции

, , R_B = 19qa/8,

, R_D = 13qa/8, строим эпюры поперечной силы Q и изгибающего момента М_F от заданной нагрузки.

Эпюра (рис. д). В сечении А, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента.

Эпюра (рис. е). Эта эпюра строится от единичного момента, приложенного в сечении Е, где ищется угол поворота.

2. Определение перемещений. Прогиб сечения А находим, пользуясь правилом Верещагина. Эпюру М_F на участках ВС и CD разбиваем на простые части (рис. г). Необходимые вычисления представляем в виде таблицы.

Номер части	1	2	3	4	5	6	7
	-qa^3/6	2qa^3/3	-qa^3/2	qa^3/4	qa^3/4	-qa^3	-qa^3/2
Ci	-3a/4	-3a/4	-5a/6	-2a/3	-a/3	-a/6	0
	qa^4/8	-qa^4/2	5qa^4/12	-qa^4/6	-qa^4/12	qa^4/6	0	-qa^4/24

Получаем .

Знак “минус” в результате означает, что точка А перемещается не вниз, как была направлена единичная сила, а вверх.

Угол поворота сечения Е находим двумя способами: по правилу Верещагина и по формуле Симпсона.

По правилу Верещагина, перемножая эпюры M_F и , по аналогии с предыдущим получим

,

.

Для нахождения угла поворота по формуле Симпсона вычислим предварительно изгибающие моменты посредине участков:

Искомое перемещение, увеличенное в EI_x раз,

.

Пример 9.

Определить, при каком значении коэффициента k прогиб сечения С будет равен нулю. При найденном значении k построить эпюру изгибающего момента и изобразить примерный вид упругой линии балки (см. рис.).

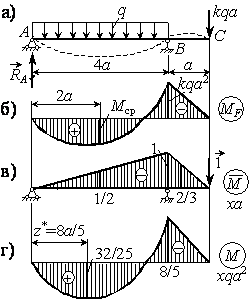
Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в сечении С, где ищется прогиб.

По условию задачи V_C = 0. С другой стороны, . Интеграл на участке АВ вычисляем по формуле Симпсона, а на участке ВС – по правилу Верещагина.

Находим предварительно

Перемещение сечения С ,

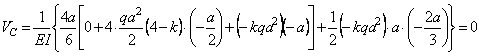
Отсюда , .

При найденном значении k определяем значение опорной реакции в точке А: , , , исходя из которого находим положение точки экстремума на эпюре М согласно условию .

По значениям момента в характерных точках

, ,

строим эпюру изгибающего момента (рис. г).

Пример 10.

Определить вертикальное перемещение точки В консольной балки, изображенной на рисунке.

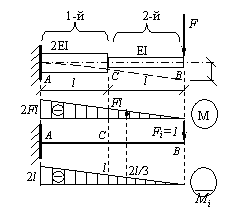
Решение.

Строим эпюру изгибающих моментов М от действия внешней сосредоточенной силы F: М_В = 0, М_А = –F2l (эпюра линейная).

По условию задачи требуется определить вертикальное перемещение у_В точки В консольной балки, поэтому строим единичную эпюру от действия вертикальной единичной силы F_i = 1, приложенной в точке В.

Учитывая, что консольная балка состоит из двух участков с разной жесткостью на изгиб, эпюры и М перемножаем с помощью правила Верещагина по участкам отдельно. Эпюры М ипервого участка перемножаем по формуле , а эпюры второго участка – как площадь эпюры М второго участка Fl²/2 на ординату 2l/3 эпюры второго участка под центром тяжести треугольной эпюры М этого же участка.

В этом случае формула дает:

Пример 11.

Определить вертикальное перемещение точки В однопролетной балки, изображенной на рисунке. Балка имеет постоянную по всей длине жесткость на изгиб EI.

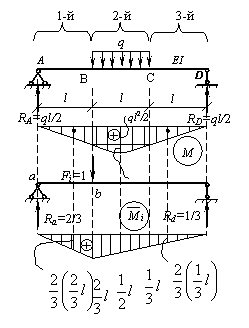
Решение.

Строим эпюру изгибающих моментов М от действия внешней распределенной нагрузки: М_А = 0; M_D = 0;

.

Прикладываем в точке В единичную вертикальную силу F_i = 1 и строим эпюру (см. рис.):

откуда R_a = 2/3;

откуда R_d = 1/3, поэтому M_a = 0; M_d = 0; .

Разделим рассматриваемую балку на 3 участка. Перемножение эпюр 1-го и 3-го участков не вызывает трудностей, так как перемножаем треугольные эпюры. Для того чтобы применить правило Верещагина ко 2-му участку, разобьем эпюру М 2-го участка на две составляющие эпюры: прямоугольную и параболическую с площадью (см. таблицу).

Центр тяжести параболической части эпюры М лежит посередине 2-го участка.

Таким образом, формула при использовании правила Верещагина дает:

Пример 12.

Определить максимальный прогиб в двухопорной балке, нагруженной равномерно распределенной нагрузкой интенсивности q (см. рис.).

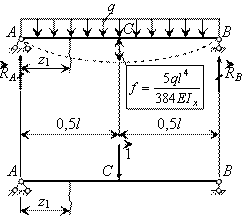
Решение.

Находим изгибающие моменты:

- от заданной нагрузки

- от единичной силы, приложенной в точке С, где ищется прогиб .

Вычисляем искомый наибольший прогиб, который возникает в среднем сечении балки

Пример 13.

Определить прогиб в точке В балки, показанной на рисунке.

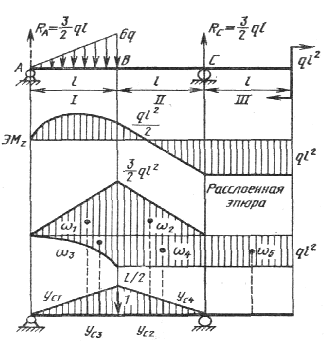
Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и единичной силы, приложенной в точке В. Чтобы перемножить эти эпюры, надо балку разбить на три участка, так как единичная эпюра ограничена тремя различными прямыми.

Операция перемножения эпюр на втором и третьем участках осуществляется просто. Затруднения возникают при вычислении площади и координат центра тяжести основной эпюры на первом участке. В таких случаях намного упрощает решение задачи построение расслоенных эпюр. При этом удобно одно из сечений принять условно за неподвижное и строить эпюры от каждой из нагрузок, приближаясь справа и слева к этому сечению. Целесообразно за неподвижное принимать сечение в месте перелома на эпюре единичных нагрузок.

Расслоенная эпюра, в которой за неподвижное принято сечение В, представлена на рисунке. Вычислив площади составных частей расслоенной эпюры и соответствующие им ординаты единичной эпюры, получаем

.

Пример 14.

Определить перемещения в точках 1 и 2 балки (рис. а).

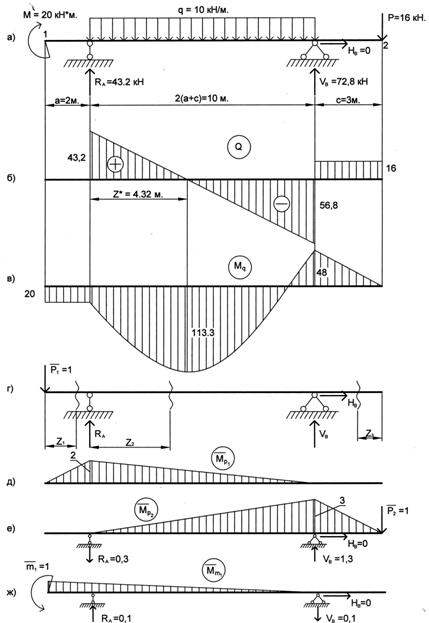
Решение.

Приведем эпюры М и Q для балки при а=2 м; q=10 кН/м; С=1,5а; М=0,5qa²; Р=0,8qa; М₀=М; =200 МПа (рис. б и в).

Далее определяем перемещения в точках 1 и 2 балки (рис. а). Состояние балки под действием заданной нагрузки обозначим q.

Определим вертикальное перемещение центра сечения, где приложен сосредоточенный момент. Для этого рассмотрим балку в состоянии под действием только сосредоточенной силы приложенной в точке 1 перпендикулярно оси балки (по направлению искомого перемещения ) (рис. г).

Вычислим опорные реакции, составив три уравнения равновесия

Проверка

Реакции найдены верно.

Для построения эпюры рассмотрим три участка (рис. г).

1 участок

2 участок

3 участок

По этим данным строим эпюру (рис. д) со стороны растянутых волокон.

Определим по формуле Мора с помощью правила Верещагина. При этом криволинейную эпюру , на участке между опорами, можно представить в виде сложения трех эпюр. Стрелка

Знак «минус» означает, что точка 1 перемещается вверх (в направлении противоположном ).

Определим вертикальное перемещение точки 2, где приложена сосредоточенная сила. Для этого рассмотрим балку в состоянии под действием только сосредоточенной силы приложенной в точке 2 перпендикулярно оси балки (по направлению искомого перемещения ) (рис. е).

Эпюра строится аналогично предыдущей.

Далее по формуле Мора

Точка 2 перемещается вверх.

Определим угол поворота сечения, где приложен сосредоточенный момент.

Для этого рассмотрим балку в состоянии под действием только сосредоточенного момента , приложенного в сечении 1 против часовой стрелки (рис. ж).

Вычислим опорные реакции, составив три уравнения равновесия.

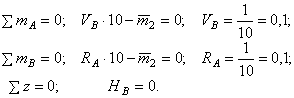
Проверка Реакции найдены верно

Эпюра показана на рис. ж.

Далее по формуле Мора

Сечение 1 поворачивается по часовой стрелке.

Пример 15.

Найдем перемещения – прогиб сечения С и угол поворота сечения В в балке, показанной на рис. 1, а, методом Максвелла – Мора и сравним их с теми же перемещениями, найденными ранее аналитическим способом.

Решение.

В соответствии с методом Максвелла – Мора перемещения находим по формуле . Рассмотрим два варианта использования этой формулы:

- аналитическое интегрирование формулы;

- интегрирование с помощью правила Верещагина.

Вариант 1. Аналитическое интегрирование формулы Максвелла – Мора

Для определения перемещений по формуле выпишем выражения для изгибающих моментов в балке от заданной нагрузки на каждом участке балки. Начало координат х можно выбирать произвольным образом, например, так, как показано на рис. 1, а.

Рис.1

Тогда выражения для изгибающих моментов на трех участках будут такими:

участок 1: ;

;

участок 2: ;

;

участок 3: ;

.

Найдем сначала угол поворота сечения В балки. Загрузим балку в сечении В единичной обобщенной силой, соответствующей искомому перемещению, то есть парой сил, равной единице (рис. 1, б). Запишем выражения для изгибающих моментов на каждом участке от единичной пары сил. Начало отсчета координаты х должно быть таким же, как при записи выражений для изгибающих моментов от заданной нагрузки (см. рис. 1, б). Тогда:

участок 1: ; ;

участок 2: ; ;

участок 3: ; .

Подставим записанные выражения в интеграл Максвелла – Мора и проинтегрируем (на первых двух участках интегралы в рассматриваемом примере равны нулю):

.

Чтобы найти прогиб сечения С , приложим в точке С новую единичную обобщенную силу – сосредоточенную силу, положив ее равной единице (рис. 1, в). Выражения для изгибающих моментов на каждом участке от единичной сосредоточенной силы будут такими:

участок 1: ; ;

участок 2: ; ;

участок 3: ; .

После подстановки функций и в интеграл и интегрирования на каждом участке получим

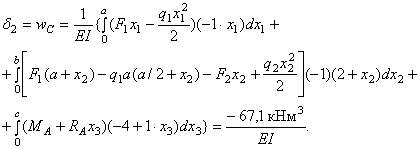
Величины найденных перемещений совпадают с результатами, полученными ранее аналитическим способом, а знак у угла поворота другой. Это следствие разных правил знаков в аналитическом методе и методе Максвелла – Мора. Обсудим полученные знаки перемещений. Положительный знак угла поворота показывает, что поворот происходит по направлению обобщенной силы. Поскольку единичная пара принята направленной по часовой стрелке, то и сечение В поворачивается по часовой стрелке. Отрицательный знак прогиба означает, что сечение С перемещается в сторону, противоположную принятому направлению единичной силы, то есть вверх. Таким образом, результаты решения полностью совпадают с полученными ранее аналитическим методом.

Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила Верещагина

Как отмечалось раньше, процесс интегрирования формулы Максвелла – Мора с помощью правила Верещагина (или Симпсона) называется "перемножением эпюр". Чтобы "перемножить эпюры", построим их. Сначала построим эпюру изгибающих моментов от заданной нагрузки (рис. 2, а). Разобьем эпюру М на 6 простых фигур: три треугольника , и , два сегмента, ограниченных квадратной параболой, и и трапецию . Порядок разбивки эпюры моментов на составляющие фигуры на втором участке поясняет рис. 3 (эпюру М на втором участке можно разбить и на две фигуры: трапецию, у которой основания имеют разные знаки (10 и –25) и сегмент . В этом случае удобно воспользоваться правилом перемножения трапеций ).

Найдем площади этих фигур:

кНм², кНм²,

кНм², кНм²,

кНм², кНм².

Рис.2

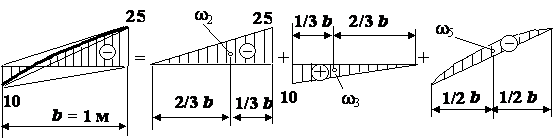
Рис.3

Для определения площадей и использована формула . Затем строим эпюры моментов от единичных обобщенных сил, соответствующих искомым перемещениям. Чтобы определить угол поворота сечения В, приложим в точке В балки пару сил, равную единице, и построим эпюру изгибающих моментов М₁ от этой пары сил (рис. 2, б). Найдем ординату под центром тяжести площади . Независимо от положения центра тяжести трапеции (а оно не определено) ордината под центром тяжести равна единице, так как изгибающий момент М₁ на участке перемножения является постоянной величиной, всюду равной единице. То есть . Поскольку на всех остальных участках изгибающий момент М₁ = 0 и , то по формуле искомое перемещение

.

Полученная величина угла поворота совпадает с найденной ранее аналитическим методом. Положительный знак говорит о том, что поворот сечения В происходит по направлению обобщенной силы, то есть в соответствии с принятым на рис. 3, б направлением единичной пары по часовой стрелке. Теперь будем искать прогиб сечения С. Загрузим балку новой обобщенной силой, соответствующей прогибу в точке С. Такой обобщенной силой будет сосредоточенная сила, равная единице и приложенная в точке С. Эпюра изгибающих моментов М₂ от этой единичной силы показана на рис. 3, в. Согласно формуле искомый прогиб

.

Найдем ординаты на эпюре М₂, расположенные под центрами тяжести шести фигур, на которые разбита эпюра М. Положение центров тяжестей всех фигур, кроме , показано на рис. 3, а. Ординату на эпюре М₂, расположенную под центром тяжести какой-то фигуры, можно найти либо из подобия треугольников, либо как изгибающий момент от единичной силы под центром тяжести рассматриваемой фигуры. Используем второй вариант вычисления ординат. Изгибающий момент под центром тяжести треугольника равен значению силы (1), расположенной слева от сечения, умноженной на плечо (4/3 м), со знаком минус. То есть

м.

Аналогично ордината под центром тяжести треугольника равна силе (1), умноженной на плечо (2 +2/3 = 8/3 м), со знаком минус. И так же для остальных фигур, положение центров тяжести которых известно:

м, м, м, м.

Поскольку положение центра тяжести трапеции не определено и невозможно в этом случае найти ординату под центром тяжести, воспользуемся на этом участке формулой перемножения трапеций :

кНм³.

Искомое перемещение – прогиб в точке С

.

Результат совпадает с найденным ранее прогибом в точке С аналитическим способом. Отрицательный знак перемещения показывает, что точка С перемещается в сторону, противоположную выбранному направлению единичной силы (см. рис. 3, в), то есть вверх.

Пример 16.

Определим угол поворота сечения А и прогиб сечения D в балке, показанной на рис. 1, а, методом Максвелла – Мора с использованием правила Верещагина (перемножением эпюр). Ранее эти перемещения были найдены аналитическим методом, сравним результаты, полученные двумя способами.

Рис.1

Решение.

Построим эпюры изгибающих моментов от заданной нагрузки (рис. 2, а) и от единичных обобщенных сил, соответствующих искомым перемещениям (рис. 2, б, в).

Рис.2

Разобьем эпюру моментов от заданной нагрузки на три треугольника и найдем их площади:

кНм²; кНм²; кНм².

Для определения угла поворота сечения А перемножим эпюры М и М₁. Для этого найдем ординаты на эпюре М₁, расположенные под центрами тяжести треугольников:

; ; .

Тогда угол поворота сечения А согласно формуле

.

Положительный знак угла поворота показывает, что поворот сечения А происходит по направлению обобщенной силы, то есть в соответствии с показанной на рис. 2, б единичной парой сил по ходу часовой стрелки. Результат совпадает с полученным ранее аналитическим способом.

Чтобы найти прогиб сечения D, используем при перемножении эпюру М₂. Ординаты на эпюре М₂ под центрами тяжести треугольников будут такими:

м; м; м.

Найдем прогиб сечения D по формуле :

.

Прогиб сечения D получился положительным. Это означает, что точка D перемещается по направлению единичной силы. Поскольку единичная сила показана на рис. 2, в направленной вниз, то и перемещение точки D происходит вниз. Полученный результат совпадает с тем, который был получен ранее аналитическим способом.

Пример 17.

Для двутавровой балки № 12 определить допускаемое значение момента из условия жесткости, если мм (рис.1).

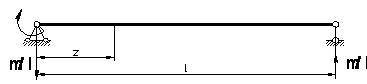
Рис.1

Решение.

Строим эпюру грузовых моментов (рис.2) и эпюру от единичной силы, приложенной в произвольном сечении (рис.3). Тогда прогиб в этом сечении

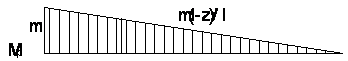
Рис.2

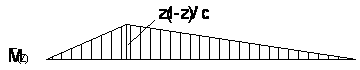
Рис.3

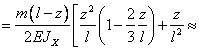
где

Проверим выполнение граничных условий. При и . Далее определяем величину максимального прогиба . Для этого необходимо решить задачу определения экстремума функции . Вычисляя производную функции и приравнивая ее нулю, получаем следующее уравнение

,

корни которого равны . Первый корень соответствует точке, лежащей вне балки, а второй

или . Условие жесткости балки при этом запишется:

Решая это неравенство относительно m, получаем

Таким образом, допускаемый момент равен

Пример 18.

Исходные данные.

, , , , жесткость балки EI_x - постоянная.

Требуется:

Определить по правилу Верещагина вертикальное перемещение точки «В»

Решение.

Определение вертикального перемещения сечения «В» выполняется в следующей последовательности:

- Строим эпюру изгибающих моментов от заданной нагрузки, то есть грузовую эпюру (рис.1, б).

- Рассматриваем единичное состояние системы: к заданной конструкции в требуемом направлении прикладываем единичную безразмерную силу в том сечении, линейное перемещение которого требуется определить (рис.1, в).

- Строим единичную эпюру, то есть эпюру изгибающих моментов от единичной нагрузки (рис.1, г).

- Приводим в соответствие участки грузовой и единичной эпюр: каждому участку грузовой эпюры должен соответствовать участок единичной эпюры, ограниченный прямой (не ломаной) линией.

В примере вдоль всей длины балки единичная эпюра ограничена прямой, однако её следует разбить на два участка, так как грузовая эпюра состоит из двух участков, площади которых и (см. рис.1, б).

- Определяем площади отдельных участков грузовой эпюры и соответствующие им абсциссы центров тяжести.

Так как участки грузовой эпюры представляют собой фигуры, площади и центры тяжести которых определить затруднительно, разобьём их на более простые составляющие с площадями , , , .

; ;

; ;

;

;

; .

- Определяем ординаты на единичной эпюре под центрами тяжести простых составляющих отдельных участков грузовой эпюры. Для определения ординат используем подобие треугольников, у которых отношения катетов равны.

;

.

Аналогично:

, .

- Записываем формулу Верещагина для рассматриваемой задачи. При этом учитываем: если грузовая и единичная эпюры на участке имеют одинаковый знак, то произведение положительно, если разный знак – отрицательно.

Если общий вид формулы Верещагина: , то для рассматриваемой задачи она принимает вид:

, .

Положительное значение указывает, что перемещение конца консоли направлено в сторону действия единичной нагрузки .

- Можно воспользоваться иным подходом для решения поставленной задачи. Ввиду того, что грузовая эпюра изгибающих моментов имеет сложные очертания, её можно «расслоить», то есть построить эпюру моментов от каждой нагрузки в отдельности (рис.1, д).

Тогда

; ; ;

; ; ;

; ; ;

; ; .

Полученный результат отличается от предыдущего на 0,8%, что лежит в пределах допустимой погрешности. При решении можно воспользоваться любым удобным для студента подходом.

Пример 19.

Для заданной стальной балки (рис.1) требуется в сечении К определить прогиб Y и угол поворота :

а) методом начальных параметров;

б) по интегралу Мора;

с) способом Верещагина.

Исходные данные: q₁ = q₂ = 2 кН/м; F = 1 кН; М = 4 кНм; a = 4 м; b = 2 м; EJ_x = const.

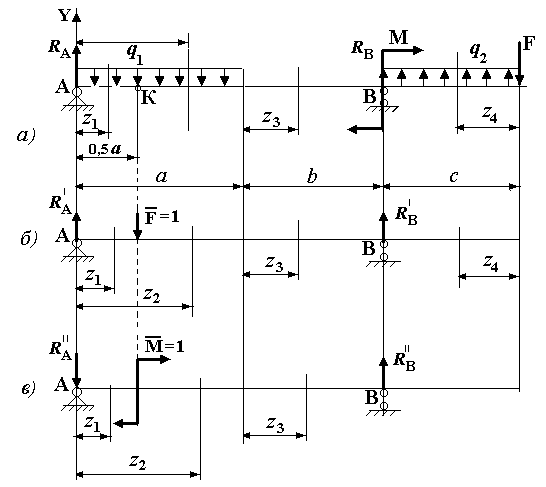
Рис.1

Решение.

1. Для определения перемещений методом начальных параметров необходимо знать все силы, приложенные к балке, в том числе и силы реакции опор.

Определяем опорные реакции:

;

= ;

;

=

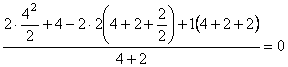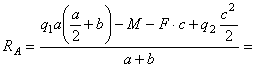
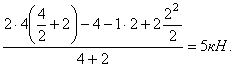
Проверка:

Расположим начало координат на левом конце балки, на опоре А (рис. 1)

Прогиб на опоре А не существует, т.е. Y₀ = 0, чтобы определить q₀ запишем прогиб на опоре В, который также равен 0, при

;

;

Определяем прогиб в сечении К:

Сечение К переместится вниз.

Определяем угол поворота сечения К:

Сечение К повернулось по часовой стрелке.

2. Для определения прогиба по интегралу Мора необходимо рассмотреть единичную балку, приложив в сечении К, (рис.1,б). Определяем для единичной балки опорные реакции по формулам:

;

;

;

Запишем в пределах каждого участка аналитические выражения

изгибающих моментов от заданных нагрузок (грузовое состояние) и от единичного момента.

Участок АК: Участок КС: ;

;

;

Участок СВ: ; Участок ДВ:

Определяем прогиб сечения К:

Сечение К переместится по направлению единичной силы, т.е. вниз. Для определения угла поворота по интегралу Мора необходимо рассмотреть единичную балку, приложив в сечении К момент, равный = 1 (рис.1,в).

Определяем для единичной балки опорные реакции и : Условия статического равновесия и дадут один результат:

Для рассмотренных ранее сечений Z запишем аналитическое выражение единичного момента.

Участок АК: Участок КС:

Участок СВ: Участок ДВ:

Определяем угол поворота сечения К:

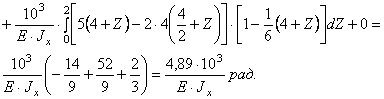
Сечение К повернулось по направлению единичного момента, т.е. по часовой стрелке.

Для определения перемещений способом Верещагина строим эпюры Q (рис. 2,б) и M (рис.2,в) для заданной балки.

Построение эпюры Q:

На участке АС в точке пересечения эпюры Q с нулевой линией на эпюре М будет максимум, найдем Z_1max:

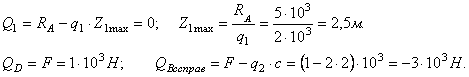
На участке DB в точке пересечения эпюры Q с нулевой линией на эпюре М будет экстремум минимум. Найдем :

Построение эпюры М:

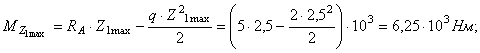
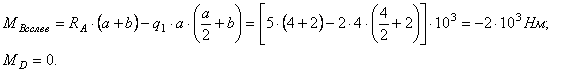
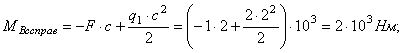
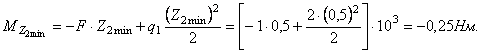
Для определения прогиба сечения К строим эпюру (рис.2, д) единичной балки, загруженной в сечении К силой, равной = 1 (рис. 2, г).

.

Разобьем площадь грузовой эпюры на простые фигуры, площадь которых можно легко определить.

Вычислим площади этих фигур и определим ординаты единичных моментов под центром тяжести каждой площади:

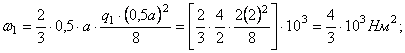
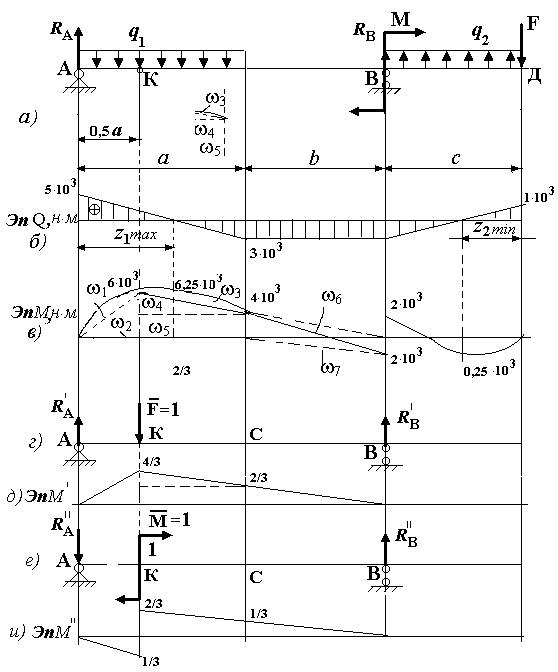
Рис. 2

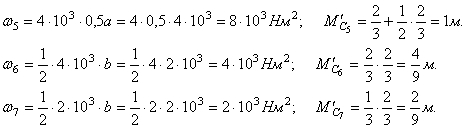
По формуле Верещагина определяем прогиб сечения К.

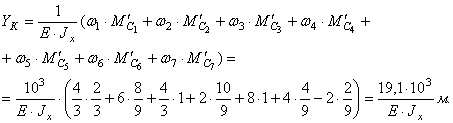
Сечение К переместилось по направлению единичной силы.

Для определения угла поворота сечения К строим эпюру (рис.2,и) для единичной балки, загруженной в сечении К моментом, равным = 1 (рис.2,е):

;

.

Площади на грузовой эпюре вычислены выше. Определим ординаты единичных моментов , расположенные напротив центров тяжести каждой площади грузовой эпюры:

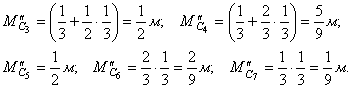
По формуле Верещагина определяем угол поворота сечения К:

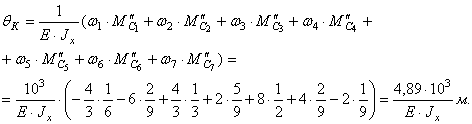
Сечение К поворачивается по часовой стрелке (по направлению единичного момента).

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00