Главная

Лекция 13. Вычислений перемещений методом Мора-Верещагина

Содержание

Формула Мора для определения перемещений в стержнях и стержневых системах

Примеры определения перемещений с помощью формулы Мора

Графоаналитический способ Верещагина и Симпсона вычисления интегралов в формуле Мора

Примеры вычисления перемещений способом Верещагина

Определение перемещений от осадки опор в балках и рамах

Определение температурных перемещений в балках и рамах

Вопросы для самопроверки

Формула Мора для определения перемещений в стержнях и стержневых системах

Современные машины и механизмы содержат большое количество высокоточных механических элементов – направляющих, осей измерительных винтов и т.д. Сохранение формы и размеров большинства из них в процессе работы является важным условием обеспечения необходимой точности измерений. В этих случаях упругие элементы машин должны удовлетворять условию жесткости

где – допускаемое перемещение (прогиб).

Для определения перемещений при изгибе используют интеграл Мора. Метод Мора является самым общим методом определения перемещений в стержневых системах. В известном смысле этот метод является универсальным, так как способен находить перемещения для различных видов деформации и в случаях сложной деформации.

При использовании этого метода (в литературе его называют: методом возможной работы; методом фиктивной нагрузки; методом единичной нагрузки) необходимо рассматривать две системы нагрузок, действующих на конструкцию. Первая система включает все реальные нагрузки, а вторая система включает только единичную нагрузку, которая действует на конструкцию. Единичная нагрузка представляет собой фиктивную или искусственно введённую нагрузку, которая позволяет определить перемещение конструкции при действии реальных нагрузок. Единичная нагрузка прикладывается в той точке конструкции перемещение которой определяем и действует в направлении искомого перемещения. Если определяется линейное перемещение, то прикладывает единичную силу, а если угловое - единицу момента сил.

Действующая на конструкцию единичная нагрузка, которая представляет собой вторую систему нагрузок, вызывает возникновение реакций опор и внутренних усилий, которые обозначим через Вместе с единичной нагрузкой и реакциями опор они образуют систему сил, которая находится в равновесии. Если конструкции предать малую возможную деформацию, в качестве которой возьмем действительные деформации конструкции, создаваемые первой системой нагрузок, то возможная работа внешних сил будет представлять собой только работу, совершаемую самой единичной нагрузкой. Эта возможная (виртуальная) работа равна произведению единичной нагрузки на перемещение , которое совершает точка её приложения; таким образом:

где величина представляет собой искомое перемещение точки конструкции за счёт реальной нагрузки.

Рассмотрим раму (рис.13.1, а), нагруженную системой внешних сил Пусть требуется определить перемещение точки A в направлении AB. Воспользуемся принципом Кастилиано. Внешняя сила в точке A в направлении AB может быть, а может и не быть. Приложим в точке A в направлении AB статически возможную силу (рис.13.1, а).

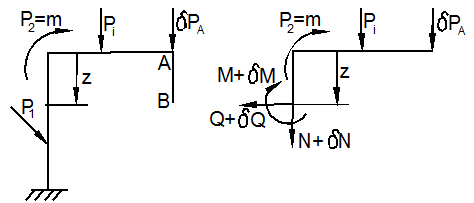
а) б)

Рис. 13.1

Тогда, согласно , имеем:

Рассечём раму в стойке на расстоянии z. В поперечном сечении возникают внутренние силовые факторы N, Q, M (рис.13.1, а). От изменения (вариации) силы в точке A в поперечном сечении рамы внутренние силовые факторы изменятся на бесконечно малые величины Эти изменения внутренних сил и моментов будут пропорциональны , т.е.

Из (2) следует, что при коэффициенты являются нормальной силой, изгибающим моментом, крутящим моментом, перерезывающими силами в сечении рамы с координатой z, которые вызваны действием единичной силы в точке A в направлении AB искомого перемещения (рис. 13.2).

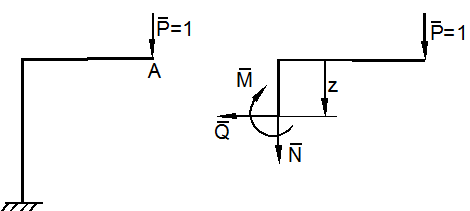
а) б)

Рис. 13.2

Так как оператор вариации имеет смысл дифференциала, то варьируя формулу потенциальной энергии

получим:

Учитывая , подставляя в и сокращая на , находим формулу

называемую формулой Мора. Она служит для определения любых обобщённых перемещений в стержневых системах.

Формулу Мора можно получить, пользуясь принципом возможных перемещений. Рассмотрим схему нагружения (см.рис. 13.2, а), когда в точке А в направлении искомого перемещения приложена единичная сила , вызывающая в поперечном сечении системы внутренние силовые факторы (рис. 13.2, б). Согласно принципу возможных перемещений работа этих внутренних силовых факторов на любых возможных перемещениях должна равняться работе единичной силы на возможном перемещении :

Выберем возможные перемещения пропорциональными действительным:

Тогда после подстановки получим:

Если учесть, что

то приходим к формуле (3).

Для систем, элементы которых работают на растяжение или сжатие (например, шарнирно-стержневые системы - фермы), в формуле Мора (3) отличен от нуля будет только слагаемое, содержащее продольные силы.

В случае пространственной работы стержня или стержневой системы, элементы которой работают, в основном, на изгиб и кручение, в формуле Мора обычно ограничиваются рассмотрением слагаемых, содержащих изгибающие и крутящие моменты.

При расчете балок или рамных систем, работающих в основном на изгиб, влияние поперечной и продольной силы на перемещение несущественно и в большинстве случаев их влияние не учитывается. В арках при определении перемещений чаще приходится учитывать все внутренние факторы и только когда ось арки близка к рациональной, то достаточно учесть нормальные усилия.

Подробно рассмотрим случай, когда брус работает только на изгиб (M_x  0, N_z = M_z = M_y = Q_x = Q_y = 0). В этой ситуации выражение (3) принимает вид:

Согласно (5) для определения перемещения произвольной точки в произвольном направлении, последовательно необходимо выполнять следующее:

1. Определить выражения для внутренних усилий M_x как функции координаты х произвольного сечения для всех участков стержневой системы от действия заданной нагрузки.

2. Исключая внешние силы и в точке, где необходимо определить перемещение по заданному направлению, прикладывается единичное усилие (сосредоточенная сила - если требуется определить линейное перемещение; сосредоточенный момент - если требуется определить угловое перемещение). На рис.13.2.1 приведены варианты приложения единичной нагрузки в зависимости от требуемой задачи: горизонтальное перемещение точки; угол поворота сечения; взаимное сближение или удаление точек; взаимный угол поворота сечений.

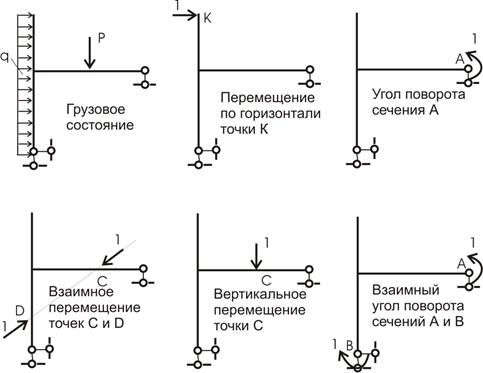
Рис.13.2.1

3. Определить выражения для внутренних усилий как функции координаты х произвольного сечения для всех участков стержневой системы от действия единичной нагрузки.

3. Найденные выражения внутренних усилий в первом и втором состоянии подставляют в интеграл Мора и интегрируют по участкам в пределах всей стержневой системы.

Полученный по формуле Мора положительный знак перемещения показывает, что искомое перемещение происходит по направлению, совпадающему с принятым направлением единичной обобщенной силы, отрицательный знак перемещения говорит о том, что точки оси перемещаются (сечения поворачиваются) в сторону, противоположную направлению единичной обобщенной силы.

Формулы Мора пригодны и для элементов, представляющих собой стержни малой кривизны, с заменой элемента длины dz в подынтегральном выражении элементом дуги ds.

Примеры определения перемещений с помощью формулы Мора

Пример 1.

Пусть требуется в простейшей ферме (рис. 13.3) определить вертикальное и горизонтальное перемещение узла А.

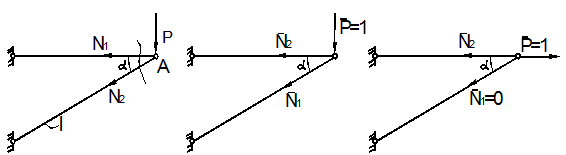
а) б) в)

Рис. 13.3

Решение.

Усилия в стержнях фермы

Формула Мора (3) имеет вид:

Усилия найдём из рис.13.3,б,в. При определении вертикального перемещения единичную силу приложим к узлу А в вертикальном направлении (рис. 13.3,б). Усилия Согласно (6) получаем:

При определении горизонтального перемещения единичную силу прикладываем к узлу A в горизонтальном направлении (рис. 7.9,в). Усилия от единичной силы Следовательно,

Пример 2.

Используя формулу Мора, найти вертикальное перемещение узла В (в мм) фермы, изображенной на рис.13.3.1,а, если жесткости стержней фермы одинаковы EA=2500 кН.

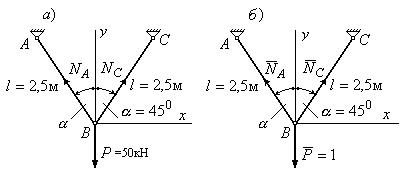
Рис.13.3.1

Решение.

1. Определяем грузовые усилия в стержнях фермы:

Из уравнения (а) устанавливаем, что . Из уравнения (б) находим:

2. Изображаем единичное состояние системы (рис.13.3.1,б) и аналогичным образом находим усилия в стержнях фермы при единичном состоянии:

3. Подставляем полученные выражения для усилий в грузовом и единичном состояниях в формулу Мора и перемножаем. Получаем:

Пример 3.

Пусть требуется определить вертикальное перемещение и угловое перемещение в точке A балки (рис. 13.4).

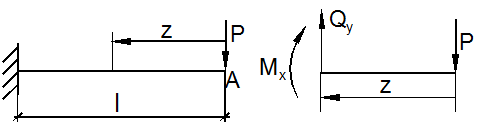
Рис. 13.4

Решение.

Для определения перемещений воспользуемся формулой Мора для обобщённых перемещений:

Из рис. 13.4 находим Найдём сначала вертикальное перемещение точки А. Приложим к балке в точке А в вертикальном направлении единичную силу 1 (рис. 13.5, а). Находим момент Подставляя значения моментов в формулу Мора (7), находим:

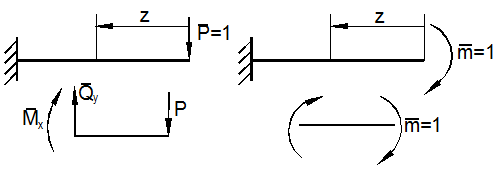
а) б)

Рис. 13.5

Знак плюс указывает на то, что перемещение произошло в том направлении, в котором действует единичная сила.

Найдём теперь угловое перемещение поперечного сечения в точке A. Приложим в точке A единичный момент (рис. 13.5,б) и определим Подставляя значения моментов в (7), получим:

Поворот сечения произошёл в том же направлении, в каком производит вращение единичный момент.

На практике использование такого подхода затруднено. Эта трудность преодолевается организацией интегрирования, интегрирование легко реализуется на компьютере.

Пример 4.

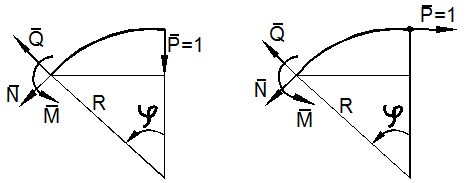
Пусть требуется определить вертикальное и горизонтальное перемещение точки A в кривом стержне (рис. 13.6, а) постоянного радиуса кривизны R.

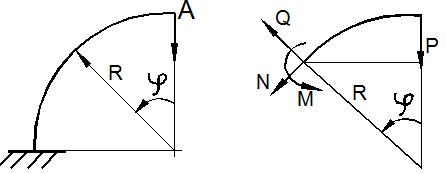
а) б)

Рис. 13.6

а) б)

Рис. 13.7

Решение.

Для определения перемещений воспользуемся формулой Мора в виде (7), пренебрегая влиянием нормальной N и перерезывающей Q сил. Изгибающий момент в произвольном сечении, определяемом углом (рис. 13.6, б), равен

Для определения вертикального и горизонтального перемещений соответственно имеем (рис. 13.7). Подставляя выражения моментов в формулу Мора в форме (7), получим:

В рассмотренном примере считается, что размеры поперечного сечения малы по сравнению с радиусом R. Это предположение позволяет использовать формулу Мора, полученную для прямого бруса, применительно к кривому брусу.

Пример 5.

Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.13.8, а), методом Мора.

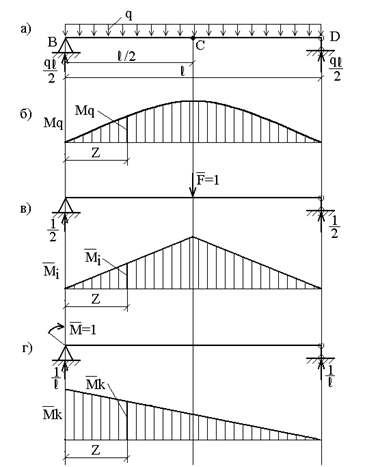
Рис. 13.8

Решение.

Рассмотрим три состояния балки: первое (грузовое) – при действии заданной распределенной нагрузки q; ему соответствует эпюра моментов (рис.13.8, б). Второе состояние (единичное) – при действии сосредоточенной силы , приложенной в точке С; ему соответствует эпюра моментов (рис.13.8, в). Третье состояние (также единичное) – при действии сосредоточенного момента , приложенного в точке В; ему соответствует эпюра моментов (рис.13.8, г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:

Вычисляем прогиб балки в точке С:

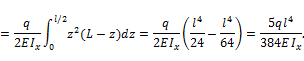
Знак "+" означает, что точка С переместится в направлении действия силы .

Вычисляем угол поворота сечения В:

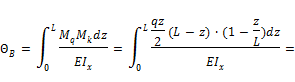
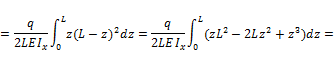
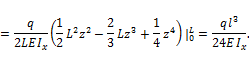
Знак "+" означает, что сечение В поворачивается в направлении действия момента то есть по часовой стрелке.

Пример 6.

Определить прогиб балки в середине пролета (рис.13.9, а) методом Мора. Оценить влияние поперечной силы на общую величину прогиба.

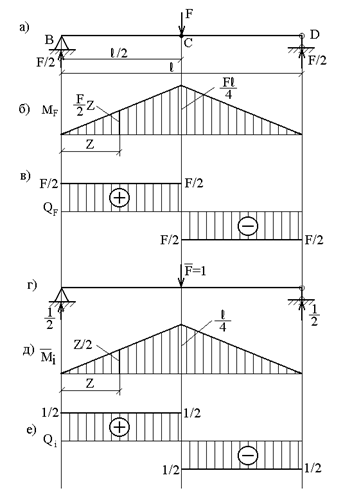
Рис. 13.9

Решение.

Рассмотрим два состояния балки. Первое состояние (грузовое) – при действии силы F (рис.13.9, а); ему соответствует эпюры изгибающих моментов (рис.13.9, б) и поперечных сил (рис.13.9, в).

Второе состояние (единичное) – при действии силы (рис.13.9, г); ему соответствуют эпюры изгибающих моментов (рис.13.9, д) и поперечных сил (рис.13.9, е).

В связи с отсутствием продольных сил в поперечных сечениях балки интеграл Мора (3) принимает вид:

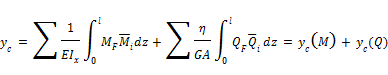
Подставляя значения изгибающих моментов и поперечных сил в сечении с координатой z (рис.13.9) для составляющих полного перемещения получим:

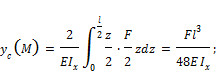
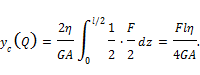
Оценим влияние поперечной силы на общую величину прогиба. Пусть рассматриваемая балка имеет прямоугольное поперечное сечение со сторонами b и h, при этом h=0,1l.

Тогда площадь сечения и его осевой момент инерции равны:

Будем считать, что ; G=0,4E тогда:

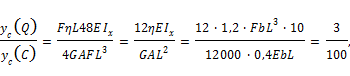
то есть прогиб, обусловленный деформацией сдвига, составляет 3% от прогиба, обусловленного изгибом. Легко убедиться, что при увеличении отношения h/L влияние поперечных сил на величину прогиба становится еще менее значительным.

Пример 7.

Для заданной балки требуется определить перемещение точки «К» в середине пролета (рис. 13.9.1,а).

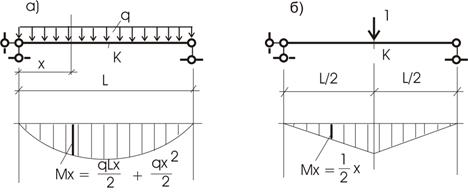
Рис.13.9.1

Решение.

Приложим силу Р = 1 в точку «К» направлением вниз, совпадающим с возможным перемещением точки «К» (рис. 156 б).

2. Построим эпюру М от грузового состояния с

3. Построим эпюру М от единичного состояния с

3. Подставляем значения моментов в выражение перемещения:

Графоаналитический способ Верещагина и Симпсона вычисления интегралов в формуле Мора

Применение метода Мора, как мы уже сумели убедиться, требует вычисления интегралов в процессе определения перемещений. В большинстве случаев при наличии большого числа участков, на которые приходится делить конструкцию, решение становится громоздким. Поэтому в практике расчетов предпочитают иметь дело с графо-аналитическими методами, позволяющими исключить интегрирование из процесса определения перемещений. Такие методы бывают не всегда точны и универсальны, но их простота и доступность делает их весьма популярными.

Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.

Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина, который предложил студент МИИЖТ Верещагин в 1924 году и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.

Докажем справедливость этого правила.

Интегралы Мора с точностью до постоянного множителя представляют собой интегралы от произведения двух функций вида:

где, по крайней мере, одна из функций (рис. 13.10)

является линейной (k,l - постоянные величины).

Возьмём к примеру, интеграл

где - момент от единичной обобщённой силы – линейная функция, - в общем случае – криволинейная функция.

Подставляя выражение для в выражение для J и производя почленное интегрирование, найдём:

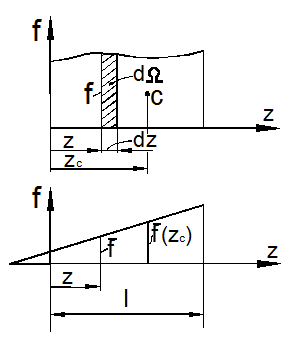
Рис. 13.10

Из рис. 13.10 следует, что есть элементарная площадь криволинейной эпюры, - статический момент этой элементарной площади относительно оси f.

Поэтому:

Из полученной формулы (8) следует простое правило вычисления интегралов Мора: интеграл с точностью до постоянного множителя равен произведению площади криволинейной эпюры f на ординату взятую из прямолинейной эпюры под центром тяжести криволинейной эпюры.

На первый взгляд, описанный графоаналитический способ вычисления интегралов Мора не даёт упрощений, т.к. всё равно приходится вычислять площадь криволинейных эпюр. Однако встречающиеся на практике эпюры могут быть разбиты на ряд простейших – прямоугольник, треугольник, симметричную квадратичную параболу и др. Эти эпюры приведены на рис. 13.11.

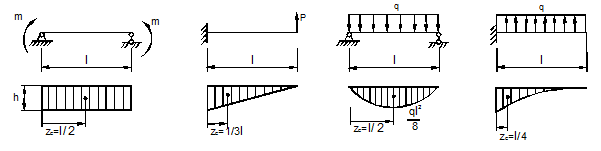
а) б) в) г)

Рис. 13.11

В первом случае во втором в третьем в четвёртом

Рассмотрим несколько сложных эпюр (рис. 13.12): а) эпюра разбивается на симметричную параболу, треугольник и прямоугольник; б) эпюра пересекает ось стержня, её можно дополнить сверху и снизу равными площадями и разложить на два треугольника, доказательство добавляемых площадей элементарно: из подобия заштрихованных треугольников следует откуда что и доказывает утверждение;

в) эпюра разбивается на симметричную параболу и два треугольника, соответствующих случаю (б).

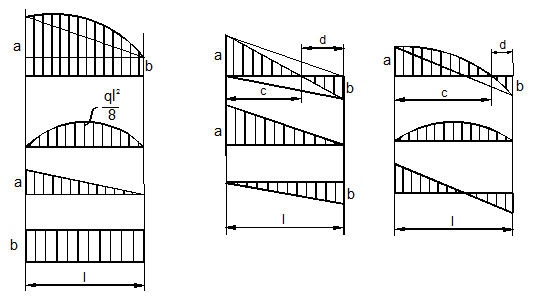
а) б) в)

Рис. 13.12

Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра является прямолинейной.

В XVIII веке английским математиком Томасом Симпсоном было предложено вычислять интегралы графическим методом, исходя из того, что интеграл представляет в пределе сумму бесконечно малых величин. Симпсон предложил разбивать площадь фигуры, образовавшуюся под кривой подинтегральной функции, на узкие полоски и суммировать площади этих полосок. Им были сформулированы соответствующие рекомендации и предложены различные формулы, позволяющие упорядочить процесс подобного интегрирования. Сложность этих формул зависела от сложности подинтегрального выражения. В большинстве случаев предложенный им подход к интегрированию дает погрешности, но существуют такие функции, интегрирование которых по способу Симпсона дает точное решение. Речь идет о гладких унимодальных функциях, порядок которых не превышает трех.

Исследуя функции, входящие в формулу Мора, можно сделать вывод, что функции изгибающих моментов, составленных для единичных состояний всегда линейны. При действии на балку распределенной нагрузки постоянной интенсивности изгибающий момент описывается кривой второго порядка. При перемножении этих функций под интегралом Мора мы получаем кривую третьего порядка. Это означает, что, если ограничить класс решаемых задач балками и рамами, нагруженными сосредоточенными силами и распределенной нагрузкой постоянной интенсивности, то при использовании для определения перемещений метода Мора-Симпсона можно получать точное решение.

Рассмотрим интегрирование по способу Симпсона функции, описываемой кубической параболой, приведенной на рис.13.12.1.

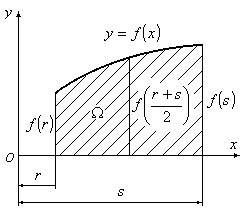
Рис.13.12.1

Формула, которой предлагается пользоваться в этом случае, имеет вид:

На рис.13.12.2 приведены грузовая (а) и единичная (б) эпюры изгибающих моментов для одного участка.

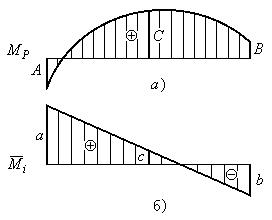
Рис.13.12.2

Буквами А, С и В обозначены изгибающие моменты на левом конце участка, посредине и на правом конце участка на грузовой эпюре. Буквами а, c и b обозначены изгибающие моменты на левом конце участка, посредине и на правом конце участка на единичной эпюре.

Интеграл Мора для одного участка имеет вид:

Произведение моментов под интегралом обозначим:

Применяя формулу Симпсона к интегралу Мора после соответствующих замен и подстановок, получим:

При решении задач с несколькими участками формула Мора-Симпсона принимает вид:

В том случае, если обе эпюры изгибающих моментов, грузовая и единичная, меняются по линейному закону и представляют собой на каждом из участков трапеции, можно исключить средние значения моментов С и с, учитывая, что они могут быть вычислены из выражений:

Подставляя эти значения в формулу (12), получаем формулу трапеций:

Применение готовых формул метода Мора-Симпсона показано в таблице 13.1. Эта таблица является весьма универсальной, так как она пригодна для определения перемещений по двум любым прямолинейным эпюрам, а также криволинейной с прямолинейной. Если любая из фигур, приведенных в табл. 13.1, перемножается с треугольником, то это перемножение сводится к трапеции, одна из ординат которых равна 0. При перемножении на прямоугольник нужно учесть, что М_a = М_b .

При помощи расчленения эпюр на части можно добиться того, чтобы при перемножении участвовали эпюры простой структуры, приведенные в таблице 13.1.

Таблица 13.1

M2(x) M1(x)
	abl

Примеры вычисления перемещений способом Верещагина

Пример 8.

Определим вертикальное перемещение точки A консольной балки (рис. 13.13, а) по формуле Мора (3) с использованием способа Верещагина.

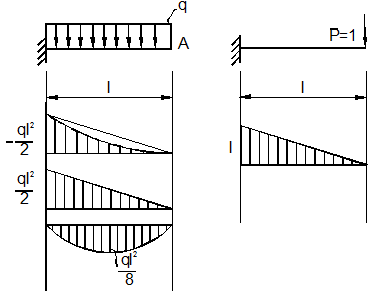
а) б)

Рис. 13.13

Решение.

С этой целью строим эпюру моментов от заданной нагрузки (рис. 13.13, б). Эпюру от заданной нагрузки разбиваем на две простейшие – треугольник и симметричную параболу. В результате имеем:

или

При перемножении площади эпюры от внешней нагрузки на ординату эпюры от единичной нагрузки следует руководствоваться правилом: если эпюры лежат по одну сторону от оси балки, то они одного знака и потому дают знак плюс. В противном случае – знак минус.

Пример 9.

Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.13.14, а), способом Верещагина.

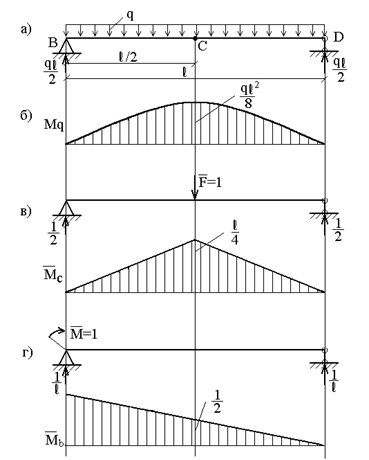
Рис. 13.14

Решение.

Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра M_q (рис.13.14, б), и два единичных состояния - при действии силы приложенной в точке С (эпюра , рис.13.14, в), и момента , приложенного в точке В (эпюра , рис.13.14, г).

Прогиб балки в середине пролета:

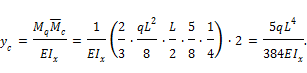
Аналогичный результат был получен ранее методом Мора (см. пример 5). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры умножить на расположенную под ее центром тяжести ординату эпюры (L/4 на рис.13.14, в), то величина перемещения будет совершенно иной и неправильной так как эпюра ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.

А при вычислении угла поворота сечения в точке В можно площадь эпюры умножить на расположенную под ее центром тяжести ординату эпюры (1/2, рис.13.14, г), так как эпюра ограничена прямой линией:

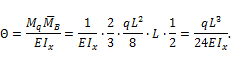
Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 5).

Пример 10.

Для балки, загруженной равномерно распределенной нагрузкой (рис. 13.15,а), требуется определить:

1. Перемещение по вертикали точки К ().

2. Перемещение по вертикали точки 3 ().

3. Угол поворота точки 3 ().

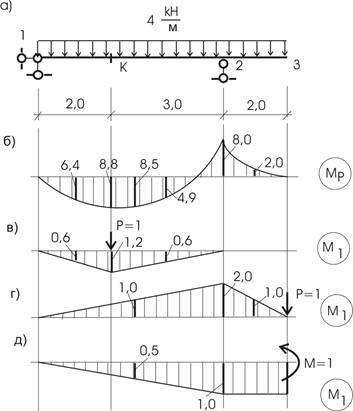
Рис.13.15

Решение.

Для нахождения этих перемещений воспользуемся первым слагаемым в формуле Мора, а именно:

Здесь М₁ – эпюра моментов от воздействия единичной нагрузки. Для первой задачи единичную нагрузку прикладываем в точку К по вертикали (рис. 13.15,в); для второй задачи – в точку 3 по вертикали (рис. 13.15,г); для третьей задачи единичную нагрузку в виде сосредоточенного изгибающего момента прикладываем к точке 3 (рис. 13.15,д) ;

М_р – эпюра изгибающих моментов от заданной внешней нагрузки (рис. 13.15,б);

EJ – жесткость балки при изгибе. Для нашего примера EJ =1.

Интеграл вычисляется либо по правилу Верещагина, либо по правилу Симпсона.

Рекомендации:

- если обе эпюры прямолинейны, то удобнее вычислять интеграл по правилу Верещагина, т. е.

- если одна из эпюр криволинейна, то удобнее интеграл вычислять по правилу Симпсона:

Необходимо помнить: если одна из эпюр на участке интегрирования имеет излом (рис. 13.15,в), то нужно интегрирование на этом участке разбить на два участка (граница участков интегрирования – точка излома).

Определение .

Перемножим М_р на М₁ (рис. 13.15,б,в).

Напоминаем правило знаков при перемножении: знак произведения положительный, если обе координаты эпюр моментов расположены по одну сторону от оси стержня.

Определение .

Перемножаем эпюру М_р (рис. 13.15,б) на эпюру М₁ (рис. 13.15,г).

Знак минус указывает, что перемещение точки 3 происходит вверх (а не вниз, как мы предполагали) на 7 единиц.

Определение .

Перемножаем эпюры моментов, показанных на рис. 13.15,б и на рис. 13.15,д. Тогда:

Пример 11.

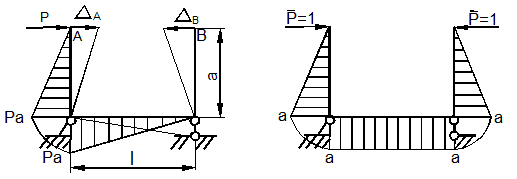
Найдём взаимное сближение точек А и В рамы (рис. 13.16, а), т.е. , используя формулу Мора и способ Верещагина.

а) б)

Рис. 13.16

Решение.

На рис. 13.16, а и б построены эпюры моментов от внешней силы и обобщённой единичной силы , где Искомое взаимное перемещение

Пример 12.

Для конструкции рамы (рис. 13.17) требуется определить горизонтальное перемещение точки 1.

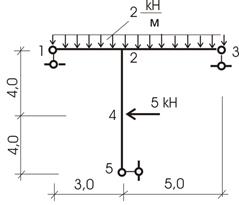
Рис.13.17

Решение.

Строим эпюру М_изг. от внешней нагрузки (рис. 13.18).

Для построения определим вертикальные опорные реакции:

отсюда находим

отсюда определяем

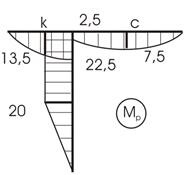
Рис.13.18

2. Построим эпюру от единичного загружения (рис. 13.19).

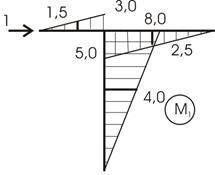
Рис.13.19

3. Вычисляем искомое перемещение:

а) по правилу Верещагина

б) по правилу Симпсона

Пример 13.

Для конструкции рамы (рис. 13.20) требуется определить:

1) вертикальное перемещение точки 2 ();

2) угол поворота сечения 4 ();

3) взаимное смещение узлов 1 и 2.

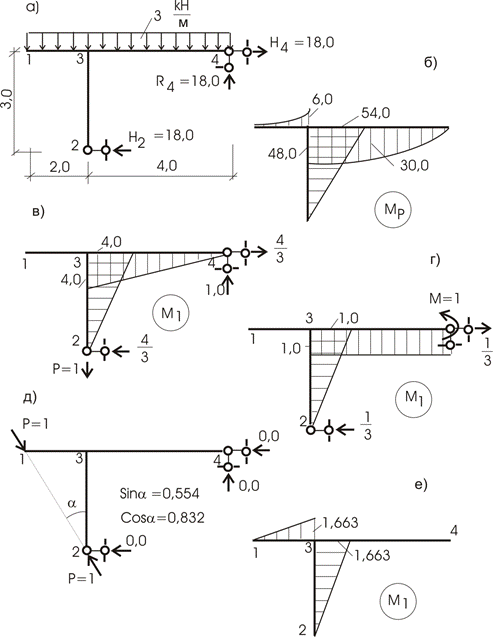
Рис.13.20

Решение.

Для решения поставленных задач построим от внешней нагрузки эпюру изгибающих моментов – М_р (рис. 13.20,б).

Задача 1. Определить вертикальное перемещение точки 2.

Строим эпюру M₁ от загружения точки 2 вертикальной силой Р = 1 (рис. 13.20,в, здесь приложение силы и эпюра моментов от этой нагрузки показаны на одном рисунке).

Перемножение эпюр произведем по правилу Верещагина и правилу Симпсона.

(по Верещагину) (по Симпсону)

Точка 2 перемещается вниз на 504 единицы.

Задача 2. Определить угол поворота сечения 4.

Прикладываем сосредоточенный изгибающий момент М = 1 к сечению 4 (рис. 13.20,г) и строим от него эпюру М₁. Перемножаем полученную эпюру М₁ на М_р (она остается прежней – рис. 13.20,б).

Задача 3. Определить взаимное смещение узлов 1 и 2.

Прикладываем к точкам 1 и 2 две единичные противоположно направленные силы, линия действия которых проходит по линии 1–2 (рис. 13.20,д). Строим от обобщенной единичной нагрузки эпюру М₁ (рис. 13.20,е).

Перемножение эпюр М₁ и М_р дает:

Пример 14.

Дана рама (рис. 13.21,а), загруженная единичной силой Р = 1 кН. Необходимо определить величину перемещения точки приложения этой силы по ее направлению.

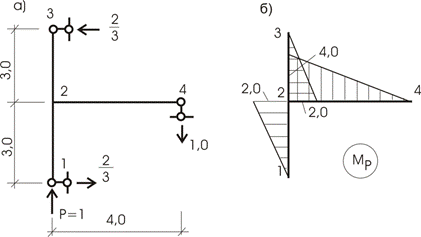
Рис.13.21

Решение.

Эпюра М_p от внешнего загружения показана на рисунке 13.21,б.

Загружаем раму единичной нагрузкой Р = 1, приложенной к точке 1 (к точке приложения внешней нагрузки) по направлению силы Р = 1 (кн) – рис. 13.22,а, и строим эпюру М₁ (рис.13.22,б). Сравнивая эти две эпюры, видим, что они равны во всех отношениях, а это означает, что формулу Мора можем записать:

В этом случае мы говорим, что эпюру перемножаем саму на себя.

Читатель, отметьте это для себя - этим мы в дальнейшем будем пользоваться неоднократно.

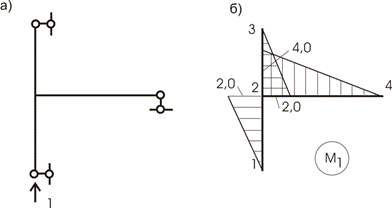
Рис.13.22

Пример 15.

Ферма (рис. 13.23,а) загружена системой сил. Требуется определить вертикальное перемещение узла 3 -

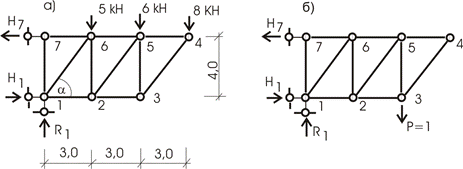
Рис.13.23

Решение.

Определяем усилия в стержнях фермы от внешнего и единичного (рис. 13.23,а,б) загружений. Результаты сведем в таблицу 13.2.

Таблица 13.2

№ стержня	1-2	2-3	3-4	5-3	5-2	2-6	6-1	1-7	7-6	6-5	5-4
Длина	3.0	3.0	5.0	4.0	5.0	4.0	5.0	4.0	3.0	3.0	3.0
Усилие Р	-16.5	-6.0	-10.0	8.0	-17.5	14.0	-23.75	0	30.75	16.5	6.0
Усилие 1	-0.75	0	0	1.0	-1.25	1	-1.25	0	1.5	0.75	0

Результат есть сумма произведений усилий N_p на N₁ и на длину стержня, соответственно.

Пример 16.

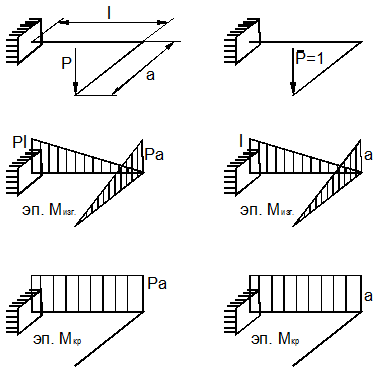
Найдём вертикальное перемещение точки пространственной рамы (рис. 13.24, а).

а) б)

Рис. 13.24

Решение.

По формуле Мора (3):

которая учитывает кручение и изгиб стержней рамы. На рис. 13.24 приведены эпюры изгибающих моментов от заданной и единичной нагрузок.

Вычисление даёт:

Определение перемещений от осадки опор в балках и рамах

Работа единичной силы (сил второго состояния) на перемещениях, вызванных осадкой опор (силами первого состояния), равна работе сил второго состояния (реакции связи) на перемещениях (осадка опор) первого состояния, т. е. перемещение в i-ом направлении вычисляется как сумма произведений реакций j связи (R_j⁽¹⁾) от единичного i-го загружения на величину перемещения j-ой связи (осадки опоры).

Пример 17.

Рассмотрим раму (рис.13.25,а). Опора 4 просела на величину . Определим горизонтальное перемещение узла 2.

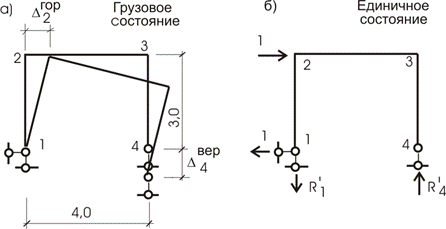
Рис.13.25

Решение.

На основании теоремы о взаимности работ запишем:

К узлу 2 приложим горизонтальную силу Р=1 (рис.13.25,б) и определим от этого загружения реакцию четвертой опоры:

откуда

Отсюда на основании формулы , определим:

Знак минус в скобках взят потому, что направления реакции и перемещения опоры различные.

Определение температурных перемещений в балках и рамах

Перемещение в балках могут вызываться не только силами, но и изменениями температуры. Предположим, что элемент конструкции нагрет неравномерно.

Рассмотрим элементарный участок dx (рис. 13.26).

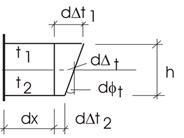
Рис.13.26

С одной стороны его мысленно закрепим глухой заделкой. От воздействия температуры волокна удлиняются (укорачиваются), вызывая деформацию стержня.

- коэффициент линейного расширения.

Тогда

Следует заметить, что оба слагаемых равноправны.

Замечание.

Правило знаков:

а) для М. Изгибающие моменты откладываем на растянутых волокнах. Если воздействие температуры и единичная сила растягивают волокна стержня с одной стороны относительно оси - знак вычисления положительный.

б) для N. Если единичное усилие и температурное воздействие растягивают (сжимают) стержень - знак произведения положительный.

Пример 18.

На конструкцию рамы (рис. 13.27,а) воздействует температура. Определим перемещение узла 3 по горизонтали.

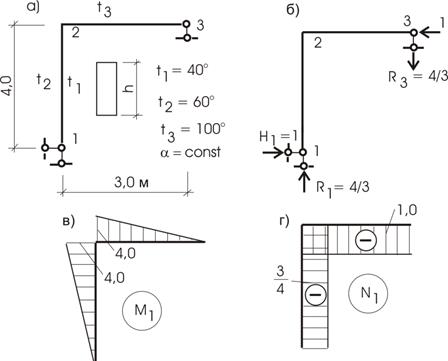
Рис.13.27

Решение.

Приложим к узлу 3 единичную силу (рис. 13.27,б). Построим эпюры моментов и продольных усилий (рис. 13.27,в,г). Перед вычислением искомого перемещения отметим правила знаков:

- для изгибающего момента: если воздействие температуры и единичная сила растягивают волокна стержня с одной стороны относительно оси, то знак вычисления положительный;

- для продольного усилия: если температура и единичная сила вызывают деформацию стержня одного направления, то знак вычисления положительный.

Вычислим искомое перемещение перемножением эпюр:

Вопросы для самопроверки

- Как записывается интеграл Мора?

- Выведите формулу перемещений Мора?

- Опишите порядок определения перемещений по Мору?

- Как определяются перемещения по правилу Верещагина?

- В какой последовательности определяют перемещения сечений балки методом Мора с использованием правила Верещагина?

- Какие ограничения накладываются на применение правила Верещагина?

- Докажите правило перемножения (сопряжения) эпюр по Верещагину?

- Опишите порядок определения перемещений по Верещагину?

- Дать обоснование определения перемещений в матричной форме?

- Какое единичное состояние образуется для балки, если необходимо определить угол поворота сечения?

- При применении формулы Верещагина какие величины необходимо знать?

- Какие величины надо знать при применении правила Симпсона?

- Можно ли определить перемещение отдельно от силы Р и нагрузки q с последующим сложением результатов?

- При вычислении перемещений по формуле Мора может ли получиться отрицательная величина?

- Какое единичное состояние необходимо, чтобы определить взаимный угол поворота примыкающих к шарниру сечений?

- Какое единичное состояние необходимо, чтобы определить вертикальное перемещение точки оси плоской рамы?

- Формула Максвелла-Мора для определения перемещений в стержневых системах. Возможные упрощения формулы Максвелла-Мора в случае расчета рам, ферм, балок.

- Способы интегрирования при расчетах по формуле Максвелла-Мора: аналитический, численный (по формуле Симпсона), графоаналитический (правило Верещагина).

- Какой принцип можно положить в основу вывода универсальной формулы Мора для определения перемещений?

- Поясните физический смысл всех компонентов, входящих в формулу Мора.

- Как записывается формула Мора при вычислении перемещений в изгибаемых системах и почему?

- Как записывается формула Мора при вычислении перемещений в фермах при действии узловой нагрузки?

- Какие два состояния системы рассматриваются при вычислении перемещений по универсальной формуле? Какие эпюры необходимо построить?

- Как перемножать эпюры по способу Верещагина?

- Можно ли применять способ Верещагина при перемножении двух полигональных эпюр, не разбивая их на простейшие фигуры?

- Когда удобно применять формулу Симпсона для перемножения эпюр?

- Какой вид имеет формула Мора для определения перемещений в балках и рамах?

- Какой вид имеет формула Мора для определения перемещений в фермах?

- Какой вид имеет формула Мора для определения перемещений в арках?

- Запишите правило Верещагина для вычисления интеграла Мора.

- Запишите формулу Симпсона для вычисления интеграла Мора.

- Какую формулу удобно применять при “умножении” трапеции на трапецию?

- Каков порядок вычисления перемещений при помощи матриц?

- Как формируют матрицы ординат единичных и грузовых эпюр моментов?

- Как формируется матрица податливости системы при вычислении перемещений?

- Какие действия нужно проделать над матрицей податливости, если в системе имеются сечения, в которых значения моментов на соседних участках одинаковы?

- Какой вид имеет окончательная запись произведения матриц при вычислении перемещений?

- Ход расчета при решении задачи об определении перемещений в стержневой системе.

- Какие виды простых деформаций в общем случае входят в полную деформацию элемента плоской стержневой системы? Пространственной стержневой системы?

- Какие комбинации простых деформаций необходимо учитывать в расчетах напряженно-деформированного состояния балок, рам (в том числе пространственных и с элементами типа затяжек, подкосов и т.п.), ферм, арок (с затяжками и без них), различных комбинированных систем?

- Какие виды деформаций для каждого из вышеуказанных типов конструкций можно не учитывать в расчете и почему?

- Чем опасно необоснованное пренебрежение тем или иным видом деформации при определении перемещений и усилий в конструкциях? В чем состоит различие в возможных последствиях этого для статически определимых и статически неопределимых систем?

- Как сказывается на результатах расчета исключение из него некоторого вида деформации – больше или меньше действительных будут вычисленные значения перемещений? А усилий? – Дайте принципиальное объяснение.

- Как учитываются разные виды простых деформаций элементов при определении перемещений линейно деформируемых стержневых систем от различных воздействий (силовых, температурных, кинематических) по методу Максвелла – Мора?

- Как сказывается на перемещениях и усилиях в конструкции податливость связей? Как при вычислении перемещений по формуле Максвелла – Мора можно учесть ее влияние?

- Перечислите основные признаки, по которым следует оценивать необходимость учитывать в расчете влияние деформации сдвига в элементах конструкции. То же, деформаций растяжения (сжатия).

- Зависит ли степень статической неопределимости системы от того, учитывается ли в расчете или нет деформация сдвига для элементов конструкции? А степень кинематической неопределимости?

- Будут ли одинаковыми или разными основные системы метода перемещений при расчете одной и той же конструкции с учетом и без учета продольных деформаций стержней (при одинаковых прочих условиях)?

- Найти с помощью метода Мора-Симпсона стрелу прогиба (в мм) балки, изображенной на рисунке, если жесткость поперечного сечения балки равна 1600 кНм².

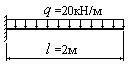
- Определить с помощью метода Мора-Симпсона угол поворота сечения А (в рад) изображенной на рисунке балки, если жесткость поперечного сечения балки EI=2000 кНм².

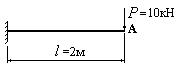
- К шарнирно опёртой разрезной балке ABC приложена распределённая нагрузка интенсивностью q. Считая известными размеры a и l, модуль Юнга E и момент инерции поперечного сечения J, определить внутренние усилия и перемещения балки с помощью метода Мора-Симпсона.

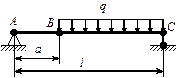
- Чему равен прогиб в точке А?

- Определить внутренние усилия и перемещения консольной балки прямоугольного сечения, нагруженной двумя силами P, модуль Юнга равен E. Размеры указаны на рисунке.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00