Главная
Лекция 5 (продолжение). Примеры решения задач по кручению
Статически определимые
задачи на кручение
Пример
№ 1
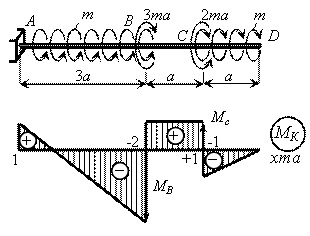
Построить эпюру Mкр для вала, изображенного на рисунке.
Решение.
На участке CD момент изменяется по линейному закону от нуля в точке D до MCD = -ma. В сечении С крутящий момент изменяется скачком на величину внешнего момента Мс, равного 2ma (скачок вверх, так как момент МС направлен против часовой стрелки). На участке ВС крутящий момент сохраняет постоянное значение, так как отсутствует погонная нагрузка (m = 0). Скручивающий момент МВ направлен по часовой стрелке, поэтому в сечении В на эпюре МК скачок происходит вниз и равен по величине МВ = 3ma. На участке АВ, нагруженном распределенной нагрузкой m, крутящий момент изменяется по линейному закону от МВА = -2ma до МАВ = МВА + m×3a = ma.
Пример № 2
Построить
эпюры крутящего момента МК
и угла закручивания ![]() для вала, приведенного
на рис. а, считая левый конец
неподвижным.
для вала, приведенного
на рис. а, считая левый конец
неподвижным.
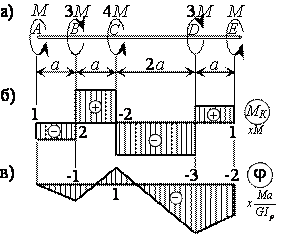
Решение.
Эпюра МК. На вал не действует распределенная нагрузка (m = 0), поэтому эпюра МК состоит из отрезков прямых, параллельных оси абсцисс. В сечениях, где к валу приложены сосредоточенные скручивающие пары, на эпюре МК наблюдаются скачки, равные приложенным моментам. Вычисляем моменты по участкам МDE = М, МCD = МDE –3М = -2М, MBC = MCD + 4M = 2M, MAB = MBC –3M = -M и строим эпюру МК (рис. б).
Эпюра
![]() . Угол закручивания изменяется по линейному закону
. Угол закручивания изменяется по линейному закону ![]() ,
поэтому для построения эпюры
,
поэтому для построения эпюры ![]() вычисляем углы поворота на границах участков,
начиная от неподвижного сечения А:
вычисляем углы поворота на границах участков,
начиная от неподвижного сечения А: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
и соединяем их отрезками прямых (см. рис. в).
Пример № 3
Определить величины и указать направления касательных напряжений, возникающих в точках А, В, С.
Дано: xA = 3 см, yA = 4 см,
xB = -1,5 см, yB = 2 см, xC = 0,
yC = -10 см.
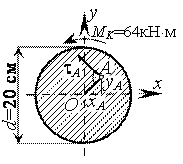
Решение.
Напряжение в
произвольной точке равно ![]() .
.
Для точки А:
![]() ,
,
![]() ,
, ![]() см4,
см4,
![]() МПа.
МПа.
Для остальных точек студенту предлагается определить самостоятельно.
Пример № 4
Определить
касательное напряжение в точке А,
если ![]() = 50 МПа.
= 50 МПа.
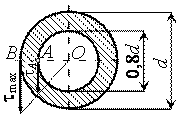
Решение.
Касательные напряжения в поперечном сечении распределяются по линейному закону, поэтому
![]() ,
,
откуда ![]() МПа.
МПа.
Пример № 5
Как изменятся
наибольшее касательное напряжение ![]() и жесткость вала,
если площадь поперечного сечения увеличить в 2 раза?
и жесткость вала,
если площадь поперечного сечения увеличить в 2 раза?
Решение.
Соотношение наибольших касательных напряжений
![]() .
.
С другой
стороны, ![]() , откуда
, откуда ![]() . Следовательно,
. Следовательно, ![]() раза. Как видим,
наибольшее касательное напряжение уменьшится в 2,83 раза.
раза. Как видим,
наибольшее касательное напряжение уменьшится в 2,83 раза.
Соотношение жесткостей
![]() ,
,
т.е. жесткость вала возрастет в 4 раза.
Пример № 6
Определить отношение диаметров двух валов из одинакового материала, передающих одинаковую мощность, если один делает П1 = 50 об/мин, а другой – П2 = 400 об/мин.
Решение.
Скручивающий
момент М связан с мощностью Р известным соотношением ![]() . Искомый диаметр из условия прочности равен
. Искомый диаметр из условия прочности равен ![]() .
Учитывая, что в данном случае МК
= М, находим
.
Учитывая, что в данном случае МК
= М, находим ![]() и
и ![]() .
.
Отношение
диаметров ![]() .
.
Как видим, увеличение скорости вращения при неизменной мощности, передаваемой валом, приводит к уменьшению диаметра и, как следствие, его массы.
Пример № 7
Два вала
одинаковой длины и массы изготовлены из одного и того же материала. Один вал
полый (![]() =0,8), а другой – сплошной. Сравнить грузоподъемность валов
при одинаковом допускаемом напряжении. Определить, насколько уменьшится масса
полого вала, если его сделать равнопрочным сплошному при одинаковой
грузоподъемности.
=0,8), а другой – сплошной. Сравнить грузоподъемность валов
при одинаковом допускаемом напряжении. Определить, насколько уменьшится масса
полого вала, если его сделать равнопрочным сплошному при одинаковой
грузоподъемности.
Решение.
1. Сравнение грузоподъемности сплошного и полого валов одинаковой массы. Вычисляем массы валов:
полого ![]() ,
,
сплошного ![]() .
.
Если массы
равны, то А1 = А2 и ![]() . (а)
. (а)
Из условия прочности находим грузоподъемности валов:
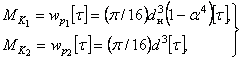 (б)
(б)
откуда их
отношение ![]() (в)
(в)
Подставляя (а) в (в), окончательно получим
![]() .
.
Следовательно, грузоподъемность полого вала при равной массе в 2,73 раза выше, чем сплошного.
2. Сравнение массы полого и сплошного валов одинаковой прочности и грузоподъемности. При одинаковой прочности и грузоподъемности из (б) имеем
![]() ,
, ![]() (г)
(г)
Отношение масс полого и сплошного валов
![]()
или с учетом
(г) ![]() .
.
Как видим, экономия материала достигает 49%.
Пример № 8
Считая величину момента М1 известной, определить при заданном соотношении диаметров ступенчатого вала величину момента М2 из условия равнопрочности тонкой и толстой частей.
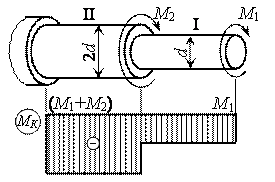
Решение.
Из эпюры МК имеем ![]() ,
, ![]() . (а)
. (а)
При равнопрочности частей
![]() или
или
![]() ,
,
откуда ![]() .
.
Следовательно, с учетом (а): М1 + М2 = 8М1 и М2 = 7М1.
Пример № 9
Сплошной вал
скручивается моментами М,
приложенными к его концам. На поверхности вала под углом 45° к
его оси установлен тензометр с базой s =
20 мм и
увеличением, равным k = 1000. Определить модуль сдвига материала,
если при увеличении крутящего
момента на величину ![]() = 16
кНм приращение показаний тензометра составило
= 16
кНм приращение показаний тензометра составило ![]() = 10 мм. Диаметр вала равен d = 10 см.
= 10 мм. Диаметр вала равен d = 10 см.

Решение.
Относительная деформация в направлении базы тензометра исходя из показаний последнего равна
![]() . (а)
. (а)
При кручении
главные напряжения равны: ![]() ,
, ![]() ,
, ![]() , поэтому на основании закона Гука
, поэтому на основании закона Гука
![]() (б)
(б)
или ![]() .
.
С другой
стороны, ![]() . (в)
. (в)
Приравнивая (а) и (б), с учетом (в) получим
![]() .
.
Отсюда
![]() = 16×103×103×20×10-3/(10×10-3×2×0,2×103×10-6)= 80 ГПа.
= 16×103×103×20×10-3/(10×10-3×2×0,2×103×10-6)= 80 ГПа.
Пример № 10
Определить
величину момента, вызывающего
разрушение чугунного вала,
если d = 75 мм, ![]() = 150 МПа,
= 150 МПа, ![]() = 600 МПа.
= 600 МПа.

Решение.
Учитывая, что
чугун является хрупким материалом, воспользуемся гипотезой прочности О.Мора,
согласно которой ![]() , где
, где ![]() . При кручении
. При кручении ![]() ,
, ![]() ,
, ![]() . Из условия прочности
. Из условия прочности ![]() или
или ![]() находим искомый разрушающий момент
находим искомый разрушающий момент
![]() кНм.
кНм.
Пример № 11
Определить из
расчета на прочность допускаемое значение М,
если ![]() = 45 МПа,
d = 10
см.
= 45 МПа,
d = 10
см.
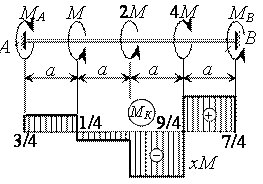
Решение.
1. Определение
реакций опор. Задача является статически неопределимой, поэтому
в дополнение к уравнению
статики ![]() , MB - MA + 3M - 4M = 0,
необходимо составить уравнение перемещений
, MB - MA + 3M - 4M = 0,
необходимо составить уравнение перемещений ![]() ,
,
![]() ,
,
откуда МВ = (7/4) М, а из уравнения статики МА = (3/4) М. Далее строим эпюру МК, из которой определяем МК max = (9/4) М.
2. Определение допустимого значения момента М.
Из условия
прочности имеем ![]() ,
,
откуда ![]() кНм.
кНм.
Пример
№ 12
Построить эпюру крутящих моментов МZ.
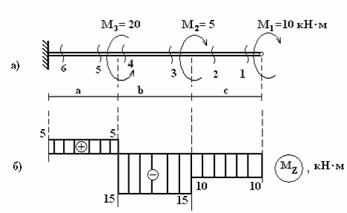
Решение:
1) Проводим ось.
2) Стержень имеет три участка загружения. Делаем сечения в начале и конце каждого участка, отбрасываем жесткую заделку и определяем МZ, Полученные положительные значения откладываем, например, вверх, отрицательные – вниз и соединяем прямой линией (см. рис.):
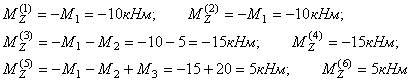
3) Ставим знак, эпюру штрихуем и обозначаем.
4)
Проверка эпюры: к стержню не приложены распределенные нагрузки, поэтому на
эпюре нет наклонных прямых. В сечении (1) приложена пара сил М1 = 10 ![]() на эпюре имеем скачок,
равный 10; на границе первого и второго
участка приложена пара сил М2 =
5
на эпюре имеем скачок,
равный 10; на границе первого и второго
участка приложена пара сил М2 =
5 ![]() на эпюре скачок 15 –
10 = 5; на границе второго и третьего участка приложена пара сил М3 = 20
на эпюре скачок 15 –
10 = 5; на границе второго и третьего участка приложена пара сил М3 = 20 ![]() на эпюре получился
скачок 15 + 5 = 20.
на эпюре получился
скачок 15 + 5 = 20.
Пример
№ 13
На вал, делающий n = 100 об/мин, передается через ведущий шкив мощность U0 = 10 кВт. С двух ведомых шкивов снимаются мощности U1 = 6 кВт и U2 = 4 кВт (см. рис.) Построить эпюру крутящих моментов Т для этого вала.

Решение.
Определяются
величины внешних скручивающих моментов по формуле ![]() :
:
![]()
![]()
![]()
Вал разбивается на два участка, границами которых являются сечения, где приложены внешние моменты. Применяя метод сечений на первом и втором участках, и пользуясь указанным выше правилом для расчета крутящего момента Т, получим
Т1 = М0 = 974 Нм; Т2 = М0 – М1 = 974 – 584 = 390 Нм.
Эпюра крутящих моментов представлена на рисунке.
Пример
№ 14
Стальной коленчатый вал ОВС (см. рис.) принимает на плечо ВС усилие F = 100 Н. Найти наибольшее касательное напряжение и угол закручивания плеча ОВ, имеющего диаметр d = 8 мм и длину l = =25мм. Модуль упругости G = 8·104 МПа, плечо а силы F равно 20 мм.
![]()
![]()

Решение.
Определим величину внешнего момента:
![]()
Поскольку к элементу ОВ больше никаких внешних сил не приложено, то, очевидно, что внутренний крутящий момент равен T = M = 2 Нм =200 Нсм.
Для вычисления
касательных напряжений и угла закручивания необходимо найти геометрические
характеристики поперечного сечения элемента ОВ.
Полярный момент сопротивления равен ![]()
Полярный момент инерции равен
![]()
Наибольшее касательное напряжение определим по формуле
![]()
Найдем угол
закручивания сечения 2 – 2 относительно сечения 1 – 1.
Как видно из рисунка, на этот же угол повернется плечо ВС. Согласно формуле ![]() , получим
, получим
![]()
Пример
№ 15
Для вала,
показанного на рисунке, сплошного круглого поперечного сечения найти
необходимые диаметры по участкам. Материал вала – сталь, модуль сдвига G = 8·104 МПа, расчетное
сопротивление на срез Rs = 30 МПа, допускаемый
угол закручивания ![]() .
.
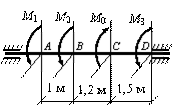
Решение.
Прежде всего строится эпюра крутящих моментов. Значения крутящих моментов по участкам следующие:
Т1 = –М1 = –0,3 кНм;
Т2 = –М1 – М2 = –0,9 кНм;
Т3 = –М1 – М2 + М0 = 1,5 кНм.
Далее
производится расчет диаметров по участкам вала из условия прочности, т.е. с
использованием формулы ![]()
![]()
![]()
![]()
Затем
рассчитываются диаметры по участкам вала из условия жесткости, т.е. с
использованием формулы ![]()
![]()
![]()
![]()
В качестве окончательных следует выбрать значения диаметров, рассчитанные из условия жесткости. Таким образом, окончательные размеры диаметров вала таковы: d1 = 52 мм, d2 = 69 мм, d3 = 78 мм.
Пример
№ 16
Для вала,
показанного на рисунке, сплошного круглого поперечного сечения рассчитать по
участкам диаметры кольцевого сечения при отношении диаметров k = dвн/d = 0,8.
Материал вала – сталь, модуль сдвига G =
8·104 МПа, расчетное сопротивление на срез Rs = 30 МПа, допускаемый угол закручивания ![]() .
.
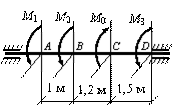
Решение.
Подставляя в формулы ![]() и
и ![]() известные значения Ti, Rs, G,
известные значения Ti, Rs, G,![]() и k найдем
и k найдем
d1,пр = 4,44·10–2 м, d2,пр = 6,36·10–2 м, d3,пр = 7,56·10–2 м;
d1,жестк. = 5,94·10–2 м, d2,жестк. = 7,84·10–2 м, d3,жестк = 8,88·10–2 м.
Таким образом, за наружные размеры диаметров участков
полого вала следует взять те,
которые были рассчитаны из условия
жесткости. Итак, d1 = 60 мм,
d2 = 79 мм, d3 = 89 мм.
Внутренние расчетные диаметры будут равны
d1,вн =
0,8·60 = 48 мм, d2,вн = 63
мм, d3,вн = 71
мм.
Примечание. Обычно внутренний канал полого вала делается постоянного диаметра, за который принимают наименьший из рассчитанных, т.е. в нашей задаче dвн = d1,вн = 48 мм, хотя при этом на некоторых участках соотношение диаметров k будет несколько отличаться от заданного.
Пример
№ 17
Прямолинейный круглый стальной стержень ступенчато-переменного диаметра жестко защемлен одним концом и нагружен системой трех внешних крутящих моментов (рис. 3.2.11, а), причем М1 = 2М; М2 = 1,5М; М3 = М, а М = 20 кНм.

Построить
эпюры крутящих моментов Т, абсолютных
![]() и относительных
и относительных ![]() углов закручивания
стержня, эпюру наибольших касательных напряжений
углов закручивания
стержня, эпюру наибольших касательных напряжений ![]() в сечениях по всей
длине стержня.
в сечениях по всей
длине стержня.
Из условий
прочности и жесткости подобрать диаметры сплошного стержня для каждого участка,
приняв в расчетах модуль сдвига G =
0,8·105 МПа, расчетное сопротивление материала стержня (сталь) на
срез Rs =
100 МПа, допускаемый относительный угол закручивания ![]() = 0,4 град/м. Полярные моменты инерции и длины участков
показаны на рис. а.
= 0,4 град/м. Полярные моменты инерции и длины участков
показаны на рис. а.
Решение.
Обозначим цифрами характерные сечения на стержне. Имеем для II и III участков
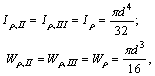 (a)
(a)
где через d обозначен диаметр стержня в
пределах этих участков. Для участка I получаем:
![]()
откуда находим
![]() (б)
(б)
Кроме того,
![]() (в)
(в)
Определим
внутренние крутящие моменты на каждом участке, начиная со свободного
конца:
TIII
= –M3 = –M; TII = –M3 + M2 = –M + 1,5M = 0,5M;
TI = –M3 + M2 – M1 = –M + 1,5M –
2M = –1,5M.
Строим
эпюру крутящих моментов Т (рис. б).
Определяем
наибольшие касательные напряжения на каждом участке, используя формулу
![]() :
:
![]()
![]()
![]()
В
последних формулах введено обозначение
![]() (г)
(г)
Строим
эпюру максимальных касательных напряжений по длине стержня (рис. в).
Определяем
углы закручивания отдельных участков по формуле ![]() :
:
![]()
![]()
![]()
где
введено новое обозначение
![]() (д)
(д)
Вычисляем
углы поворота характерных сечений стержня:
![]()
![]()
![]()
![]()
По полученным
результатам строим эпюру ![]() (рис. г).
(рис. г).
Определяем
относительные углы закручивания на каждом участке стержня по формуле ![]() :
:
![]()
![]()
![]()
Строим
эпюру ![]() (рис. д).
(рис. д).
По эпюре ![]() (рис. в) видно, что
самое большое касательное напряжение будет на участке III, поэтому формулу
(рис. в) видно, что
самое большое касательное напряжение будет на участке III, поэтому формулу ![]() записываем
применительно к этому участку
записываем
применительно к этому участку
![]()
По эпюре ![]() очевидно, что самый
большой относительный угол закручивания будет на участке III,
поэтому применяем формулу
очевидно, что самый
большой относительный угол закручивания будет на участке III,
поэтому применяем формулу ![]() для участка III:
для участка III:
![]()
Сравнивая
результаты расчетов на прочность (d = 0,1 м) и на жесткость (d = 0,14 м) находим, что главенствующим в
рассматриваемой задаче является расчет на жесткость, поскольку d =
0,14 м > 0,1 м. Окончательно принимаем d = 14 см.
Определяем
диаметры сечений остальных участков:
dII = dIII = d =14 см,
dI =1,19d = 16,7 см.
Определим значение угла
закручивания ![]() на правом торце
стержня (рис. а) в сечении 3. Из
эпюры
на правом торце
стержня (рис. а) в сечении 3. Из
эпюры ![]() (рис. г) выписываем с учетом формул (д) и (а):
(рис. г) выписываем с учетом формул (д) и (а):
![]()
Пример
№ 18
Имеется
стержень, расчетная схема которого представлена на рис. 1, а. Стержень нагружен внешними парами M1, M2, M3. Левый участок
стержня выполнен из чугуна и имеет прямоугольное сечение с заданным
соотношением сторон ![]() ; правый участок выполнен из стали имеет круглое сечение.
Известны характеристики прочности материалов:
; правый участок выполнен из стали имеет круглое сечение.
Известны характеристики прочности материалов: ![]() (
(![]() ) для чугуна и
) для чугуна и ![]() для стали; упругие
постоянные материалов -
для стали; упругие
постоянные материалов - ![]() ,
, ![]() ; допускаемый погонный угол закручивания
; допускаемый погонный угол закручивания ![]() .
.
Требуется:
1) подобрать размеры поперечных сечений стержня так, чтобы выполнялись условия прочности и жесткости на каждом участке стержня;
2) построить эпюру изменения угла закручивания по длине стержня.
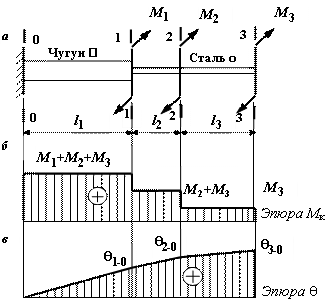
Рис.1
Решение.
Строим эпюру крутящих моментов, используя метод сечений.
Крутящий момент на каждом участке находим как алгебраическую сумму моментов
внешних пар, расположенных справа от сечения. (В этом случае можно построить
эпюру Мк без определения реактивного момента,
возникающего в защемлении.) Крутящий момент на крайнем правом участке равен ![]() , на среднем -
, на среднем - ![]() и на левом -
и на левом -![]() . Эпюра крутящих моментов показана на рис. 1, б.
. Эпюра крутящих моментов показана на рис. 1, б.
Подбираем
размеры сечения стержня из условия прочности. На чугунном участке стержня ![]() и из условия прочности
и из условия прочности
![]() , определяя
, определяя ![]() по формуле
по формуле ![]() , находим минимально необходимую величину момента
сопротивления кручению:
, находим минимально необходимую величину момента
сопротивления кручению: ![]() и, зная
и, зная ![]() , определяем ширину сечения
, определяем ширину сечения ![]() из формулы
из формулы ![]() :
: 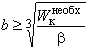 . (Значение
. (Значение ![]() высчитываем либо по
второй теории прочности
высчитываем либо по
второй теории прочности ![]() , либо по
, либо по ![]() – теории Мора.)
– теории Мора.)
Для стального
участка опасным является сечение, где действует максимальный крутящий момент,
т.е. в данном примере ![]() , и из условия прочности
, и из условия прочности ![]() находим требуемый
полярный момент сопротивления
находим требуемый
полярный момент сопротивления
![]() ,
,
где ![]() определяем по теориям
прочности, справедливым для пластичного материала
определяем по теориям
прочности, справедливым для пластичного материала ![]() или
или ![]() . Зная
. Зная ![]() , ищем радиус поперечного сечения, используя формулу
, ищем радиус поперечного сечения, используя формулу ![]() для полярного момента
сопротивления
для полярного момента
сопротивления
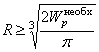 .
.
Полученные размеры рекомендуем округлить в большую сторону до 0,1 мм.
Проверим,
выполняется ли для найденных из условия прочности размеров поперечных сечений
условие жесткости. Сосчитаем геометрические характеристики ![]() и
и ![]() по формулам
по формулам ![]() и
и ![]() и модули сдвига чугуна
и стали по
и модули сдвига чугуна
и стали по ![]() . На чугунном участке
стержня должно выполняться условие
. На чугунном участке
стержня должно выполняться условие
![]() .
.
На стальном участке должно быть
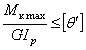 .
.
Если условие жесткости на каком-то участке не выполняется, то следует увеличить размеры сечения. Из условия жесткости находим минимально необходимую геометрическую характеристику жесткости для прямоугольного сечения:
![]()
и требуемый полярный момент инерции для круглого сечения
![]() .
.
Зная ![]() и
и ![]() , определяем по формулам
, определяем по формулам ![]() и
и ![]() размеры поперечного
сечения, удовлетворяющие условию жесткости
размеры поперечного
сечения, удовлетворяющие условию жесткости
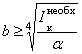 и
и 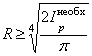 .
.
Окончательно размеры, удовлетворяющие двум условиям (и условию прочности, и условию жесткости), и соответствующие им геометрические характеристики сечений используем в дальнейших расчетах.
Построим эпюры
касательных напряжений в поперечных сечениях стержня (рис. 2 и рис.3),
сосчитав значения напряжений по формуле ![]() для круглого сечения и
по формулам
для круглого сечения и
по формулам ![]() ,
, ![]() для прямоугольного
сечения.
для прямоугольного
сечения.
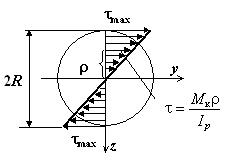
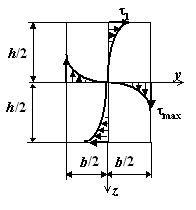
Рис.2
Рис.3
Заметим, что
по найденным значениям напряжений можно проверить свои вычисления, а именно,
если размеры сечения были определены из условия прочности, то значения
максимальных касательных напряжений должны быть близки к допускаемым. Если же
размер сечения находился из условия жесткости, то максимальные напряжения будут
меньше допускаемых касательных напряжений.
Построим эпюру
углов закручивания. Углы закручивания на каждом участке стержня вычисляются по
формулам ![]() или
или ![]() . При этом
следует учитывать знак крутящего момента. Построение эпюры углов закручивания
следует начинать, определив угол закручивания
. При этом
следует учитывать знак крутящего момента. Построение эпюры углов закручивания
следует начинать, определив угол закручивания ![]() сечения 1–1 (рис. 1, а) по отношению к неподвижному сечению 0–0 (заделке).
Например, в рассматриваемом примере
сечения 1–1 (рис. 1, а) по отношению к неподвижному сечению 0–0 (заделке).
Например, в рассматриваемом примере
![]() .
.
Угол
закручивания ![]() сечения 2–2 по
отношению к сечению 1–1 найдем по формуле
сечения 2–2 по
отношению к сечению 1–1 найдем по формуле ![]() :
:
![]() .
.
Аналогично
находится угол закручивания ![]() сечения 3–3 по
отношению к сечению 2–2. На эпюре
сечения 3–3 по
отношению к сечению 2–2. На эпюре ![]() откладываем полные
углы закручивания сечений по отношению к неподвижному сечению, т. е.
откладываем полные
углы закручивания сечений по отношению к неподвижному сечению, т. е.
![]() ,
,
![]() .
.
Вид эпюры
углов закручивания зависит от того, найдены ли размеры поперечного сечения из
условия прочности или из условия жесткости. На рис. 1, в показан вид эпюры ![]() , построенной в предположении, что размеры поперечных сечений
найдены из условия прочности. В этом случае угол наклона эпюры
, построенной в предположении, что размеры поперечных сечений
найдены из условия прочности. В этом случае угол наклона эпюры ![]() на каждом участке
прямо пропорционален величине крутящего момента и обратно пропорционален
жесткости стержня при кручении (GIp,
GIк). Если размеры сечений
на всех участках получены из условия жесткости, то угол наклона эпюры q на
опасных участках должен быть одинаковым.
на каждом участке
прямо пропорционален величине крутящего момента и обратно пропорционален
жесткости стержня при кручении (GIp,
GIк). Если размеры сечений
на всех участках получены из условия жесткости, то угол наклона эпюры q на
опасных участках должен быть одинаковым.
Пример
№ 19
Стальной вал
переменного сечения (G = 8×104
МПа; ![]() ,
, ![]() = 120 МПа), испытывает
кручение от приложенных к нему трех известных моментов М1, М2,
М3 и одного
неизвестного
= 120 МПа), испытывает
кручение от приложенных к нему трех известных моментов М1, М2,
М3 и одного
неизвестного ![]() (рис. 1, а).
(рис. 1, а).
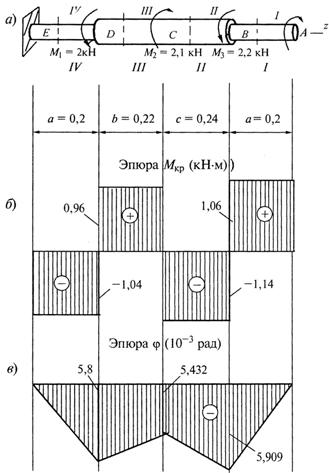
Рис.1
Требуется:
1) установить при каком значении момента Х угол поворота правого концевого сечения вала равен нулю;
2) для найденного значения Х построить эпюру крутящих моментов;
3) определить
размеры поперечного сечения вала из условий прочности и жесткости, приняв, что
участки длиною ![]() – имеют диаметр d1, а
– имеют диаметр d1, а ![]() и
и ![]() – диаметр d2, и
– диаметр d2, и ![]() ;
;
4) показать распределение касательных напряжений в поперечных сечениях;
5) построить эпюру углов закручивания.
Решение.
Силовой участок – это участок вала между двумя
внешними моментами.
Для определения величины неизвестного момента Х
выразим угол поворота свободного конца (сечение А) через действующие
моменты и приравняем его нулю.
Для этого применим принцип независимости
действия сил, который для нашего случая формулируется так: для того, чтобы
вычислить угол поворота ![]() от группы моментов
нужно вычислить этот угол от каждого сосредоточенного момента, действующего
отдельно, и все результаты алгебраически сложить.
от группы моментов
нужно вычислить этот угол от каждого сосредоточенного момента, действующего
отдельно, и все результаты алгебраически сложить.
При действии только сосредоточенного момента Х
кручению подвергаются все участки вала. Используя ![]() получим
получим
![]()
При действии только момента ![]() кручению подвергается четвертый
участок – поворачивается сечение D,
а вслед за ним на тот же угол поворачивается остальные участки без деформации
кручению подвергается четвертый
участок – поворачивается сечение D,
а вслед за ним на тот же угол поворачивается остальные участки без деформации ![]() .
.
Таким же путем находим
![]() ;
;
![]() .
.
Окончательно,
![]() .
.
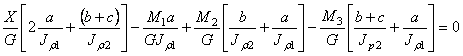 ;
;
Учтем, что ![]()
при ![]()
Умножив
обе части расчетного уравнения на ![]() , получим
, получим
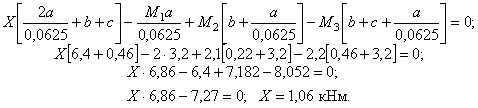
II.
Построение эпюры крутящих моментов с учетом Х
Определим крутящий момент на каждом силовом
участке, применив метод сечений:
Мкр1 = X = 1,06 кНм;
Мкр2 = Х – М3 = 1,06 – 2,2 = –1,14 кНм;
Мкр3 = Х – М3 +М2 = 1,06 – 0,1 = 1,05
кНм;
Мкр4 = Х – М3 +М2 – М1
= 1,06 – 2,1 = –1,04 кНм.
По полученным значениям крутящих моментов строим
эпюру Мкр (рис. 1, б).
III. Определение размеров поперечных сечений вала
Расчет
на прочность
На участках I и IY круглые поперечные сечения
одинаковые с диаметром ![]() . Наиболее опасным из этих двух участков является участок I
. Наиболее опасным из этих двух участков является участок I ![]() .
.
![]()
На участках II
и III – сечение диаметром ![]() . Наибольший по модулю момент
. Наибольший по модулю момент ![]() на участке II.
на участке II.
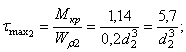
Таким образом, для всего вала опасным по прочности является I участок.
Находим
диаметр ![]() из условия прочности
из условия прочности
![]()
Отсюда 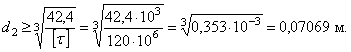
Расчет на жесткость
Выражаем
относительные углы закручивания через ![]() .
.
![]()
![]()
![]()
![]()
Следовательно, на первом участке имеет место максимальный угол закручивания.
По условию жесткости, переведя градусы в радианы, получим
![]()
![]()
![]()
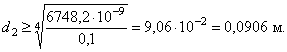
Из условий
прочности и жесткости ![]() . Округляем до целых мм:
. Округляем до целых мм:![]() , отсюда
, отсюда ![]()
IV. Построение эпюр касательных напряжений ![]() в поперечных сечениях
вала (рис.2)
в поперечных сечениях
вала (рис.2)
Сечение I-I

Сечение II-II
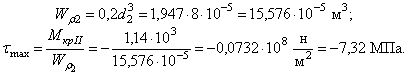
Сечение III-III
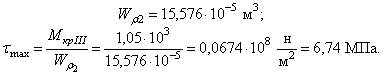
Сечение IY-IY
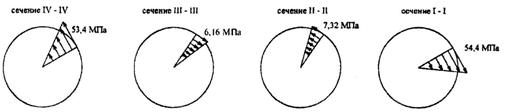
Рис.2
Y. Построение эпюры узлов поворота сечений вала
Полярные моменты инерции сечений для:
участков I и
IY ![]()
участков II и
III ![]()
Жесткость сечений на кручение
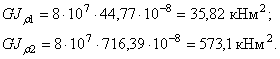
Углы поворота
отдельных сечений вала определяются по отношению к неподвижному сечению (в
нашем случае жесткая заделка) ![]()
![]()
![]()
![]()
![]()
Ошибка
составляет ![]() .
.
По вычисленным
значениям ![]() строим эпюру углов
закручивания (рис. 1, в). Так как
крутящие моменты на всех участках постоянны, то ординаты эпюры углов
закручивания линейно зависят от координаты Z – расстояние от начала участка до
сечения
строим эпюру углов
закручивания (рис. 1, в). Так как
крутящие моменты на всех участках постоянны, то ординаты эпюры углов
закручивания линейно зависят от координаты Z – расстояние от начала участка до
сечения
![]()
Пример №20
Для вала, подобрать поперечное
сечение круглой, кольцевой и прямоугольной форм, если Т1 =600 Нм,
Т2 =1000 Нм, Т3 = =800Нм, Т4 = 1300 Нм, Т5 =1600Нм, ![]() = 0,7 , h/b = 2,
= 0,7 , h/b = 2, ![]() = 100
МПа. Построить эпюру углов закручивания для вала круглого поперечного сечения.
= 100
МПа. Построить эпюру углов закручивания для вала круглого поперечного сечения.
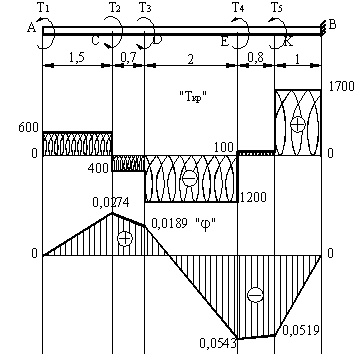
Решение.
1) Строим эпюру крутящего момента со свободного конца вала и определяем опасное сечение
АС
![]()
СD
![]()
DЕ
![]()
ЕК
![]()
КВ
![]()
Из эпюры крутящих моментов видно, что опасным, является участок КВ, максимальное значение крутящего момента Ткр max= 1700 Нм.
2) Подбираем поперечное сечение вала
2.1) Круглое сечение
Условие прочности при кручении:
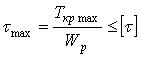
![]()
![]()
Принимаем d = 45 мм.
2.2) Кольцевое сечение
![]()
![]()
Принимаем D = ![]() мм.
мм.
2.3) Прямоугольное сечение
![]()
Для прямоугольного сечения с отношением ![]() .
.
![]()
Тогда ![]() м.
м.
3) Строим эпюру углов закручивания
Найдем момент инерции для круглого сечения:
![]() м4.
м4.
![]()
![]()
![]()
![]()
![]()
4) Сравним веса валов
Найдем площадь поперечного сечения для каждого из валов: круглого, кольцевого, прямоугольного.
![]()
![]()
![]()
![]()
Пример
№ 21
Для заданного ступенчатого стального вала подобрать поперечные сечения и построить:
- эпюру крутящих моментов;
- эпюру углов закручивания;
- эпюру касательных напряжений по длине вала;
- эпюру касательных напряжений для опасного сечения.
![]() МПа;
МПа; ![]() м;
м; ![]() кНм;
кНм; ![]() кНм;
кНм; ![]() кНм;
кНм; ![]() МПа
МПа
Сечение подобрать из условий прочности и жесткости при кручении.
Допускаемый угол закручивания принять
![]() , или
, или ![]() .
.
Решение.
Расчет
начинаем с определения вращающего момента ![]() (рис. 1).
(рис. 1).
Из уравнения
равновесия:
![]() ;
;
![]() ;
;
![]() кНм.
кНм.
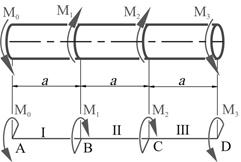
Рис.1
Для построения эпюр крутящих моментов делим вал на участки по местам приложения сосредоточенных моментов и по местам изменения поперечного сечения.
Используя метод сечений, определим крутящие моменты на каждом участке. Для этого мысленно разрежем поперечным сечением рассматриваемый участок и отбросим одну из частей вала. Воздействие отброшенной части на рассматриваемую оставшуюся часть заменим неизвестным крутящим моментом, который находим из условия равновесия.
1-й участок.
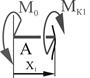
Рис.2
Возьмем
произвольное поперечное сечение на расстоянии ![]() от начала участка
(рис.2) и рассмотрим часть
вала слева от сечения. Действие правой части на левую заменяем неизвестным
крутящим моментом
от начала участка
(рис.2) и рассмотрим часть
вала слева от сечения. Действие правой части на левую заменяем неизвестным
крутящим моментом ![]() . Крутящий
момент
. Крутящий
момент ![]() направляем таким образом, что бы при
рассмотрении участка вала со стороны сечения он действовал по часовой стрелке.
направляем таким образом, что бы при
рассмотрении участка вала со стороны сечения он действовал по часовой стрелке.
Правило направления крутящего момента совершенно условно и необходимо лишь для того, что бы при рассмотрении вала, как справа, так и слева от сечения мы получали одинаковые знаки крутящего момента.
![]()
![]()
![]() , кН·м
, кН·м
Значение
крутящего момента в данном выражении не зависит от значения ![]() , поэтому для любого поперечного сечения на первом участке
значение крутящего момента будет равно
, поэтому для любого поперечного сечения на первом участке
значение крутящего момента будет равно ![]() .
.
2-й участок.
Возьмем
произвольное сечение на расстоянии ![]() от начала второго
участка (Рис.3) и рассмотрим часть вала слева от сечения.
от начала второго
участка (Рис.3) и рассмотрим часть вала слева от сечения.
Рис.3
Действие
правой части на левую заменяем неизвестным крутящим моментом ![]() .
.
![]()
![]()
![]() , кН·м
, кН·м
Значение
крутящего момента в данном выражении не зависит от значения ![]() , поэтому для любого поперечного сечения на втором участке
значение крутящего момента будет равно
, поэтому для любого поперечного сечения на втором участке
значение крутящего момента будет равно ![]() .
.
3-й участок.
Для нахождения
крутящего момента на третьем участке возьмем произвольное поперечное сечение на
расстоянии ![]() от правого конца
третьего участка и рассмотрим часть вала справа от сечения (рис.4). Действие
правой части на левую заменяем неизвестным крутящим моментом
от правого конца
третьего участка и рассмотрим часть вала справа от сечения (рис.4). Действие
правой части на левую заменяем неизвестным крутящим моментом ![]() .
.
Рис.4
![]()
![]()
![]() , кН·м
, кН·м
Значение
крутящего момента в данном выражении не зависит от значения ![]() , поэтому для любого поперечного сечения на третьем участке
значение крутящего момента будет равно
, поэтому для любого поперечного сечения на третьем участке
значение крутящего момента будет равно ![]() .
.
По найденным
значениям строим эпюру крутящих моментов (рис.5). Для этого берем нулевую
(базовую) линию параллельную оси вала и перпендикулярно ей откладываем в
масштабе значения крутящих моментов на соответствующих участках. Внутри эпюры
проставляются знаки откладываемых значений, после чего выполняется штриховка
перпендикулярно нулевой линии. Вне поля эпюры указываются значения крутящих
моментов. Слева от эпюры в кавычках указывается название эпюры («![]() ») и через запятую проставляются единицы измерения (кН·м).
Для контроля правильности построения эпюры «
») и через запятую проставляются единицы измерения (кН·м).
Для контроля правильности построения эпюры «![]() » необходимо учесть, что в местах приложения сосредоточенных
вращающих моментов на эпюре «
» необходимо учесть, что в местах приложения сосредоточенных
вращающих моментов на эпюре «![]() » должны быть скачки на величину этих моментов.
» должны быть скачки на величину этих моментов.
После
определения крутящих моментов исходя из условия прочности можно определить
требуемый диаметр вала для каждого участка, после чего принять большее
ближайшее значение из стандартного ряда (При значении диаметра вала ![]() мм необходимо
округлять требуемый диаметр в большую сторону до значения кратного
мм необходимо
округлять требуемый диаметр в большую сторону до значения кратного ![]() мм – до значения кратного
мм – до значения кратного
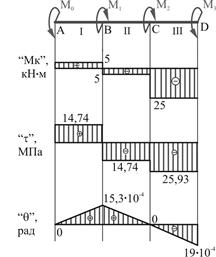
Рис.5
Условие прочности при кручении:
![]()
![]() (1)
(1)
где ![]() – крутящий
момент в поперечном сечении (подставляется абсолютное значение);
– крутящий
момент в поперечном сечении (подставляется абсолютное значение);
![]() - полярный
момент сопротивления сечения, для круглого поперечного сечения:
- полярный
момент сопротивления сечения, для круглого поперечного сечения:
![]() (2)
(2)
Из (1) с учетом (2):
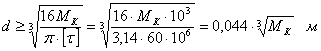
Соответственно для каждого из участков:
![]()
Принимаем ![]() ;
;
![]()
Принимаем ![]() ;
;
![]()
Принимаем ![]()
Теперь подберем диаметр вала из условия жесткости
![]() , (3)
, (3)
Для круглого вала
![]() (4)
(4)
Из (3) с учетом (4)
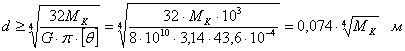
![]()
Принимаем ![]()
![]()
Принимаем ![]()
![]()
Принимаем ![]()
Из двух найденных значений диаметров следует принять больший. Окончательно принимаем
![]() ;
; ![]() ;
; ![]()
По формуле (3) с учетом (4) определяем относительный угол закручивания по отдельным участкам вала
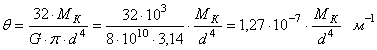
![]()
![]()
![]()
После подбора поперечного сечения выполним эскиз вала (рис.6).
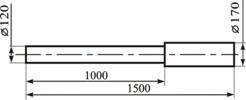
Рис.6
Максимальные касательные напряжения на участках:
![]()
![]()
![]()
Строим эпюру распределения максимальных касательных напряжений по длине вала (рис.5)
Для построения эпюры углов поворотов сечений предварительно необходимо определить углы закручивания участков:
![]() (5)
(5)
где ![]() – длина участка.
– длина участка.
Знак угла закручивания участков принимаем такой же, как и у крутящего момента.
![]()
![]()
![]()
При построении
эпюры углов поворотов сечений примем для сечения в точке ![]() угол поворота сечения:
угол поворота сечения:
![]()
Тогда остальные
сечения, относительно сечения в точке ![]() будут повернутые на
какие то углы.
будут повернутые на
какие то углы.
Сечение в
точке ![]() повернется
относительно сечения в точке А на угол закручивания первого участка:
повернется
относительно сечения в точке А на угол закручивания первого участка:
![]()
Сечение в
точке ![]() повернется
относительно сечения в точке А на
сумму углов закручивания первого и второго участков:
повернется
относительно сечения в точке А на
сумму углов закручивания первого и второго участков:
![]()
Соответственно
для сечения в точке ![]() :
:
![]()
Поскольку в
пределах каждого участка ![]() , то угол закручивания на каждом участке изменяется по
линейному закону, поэтому эпюра углов поворотов сечений будет ограничена
прямыми линиями, соединяющими значения углов поворотов сечений в точках
, то угол закручивания на каждом участке изменяется по
линейному закону, поэтому эпюра углов поворотов сечений будет ограничена
прямыми линиями, соединяющими значения углов поворотов сечений в точках ![]() ,
, ![]() ,
, ![]() и
и ![]() (рис.5).
(рис.5).
Пример
№ 22
Стальной вал переменного сечения, испытывающего кручение, закручивается крутящими моментами, действующими в двух крайних и двух пролетных сечениях. Расчетная схема вала, ее геометрические размеры, величины и точки приложения внешних крутящих моментов указаны на рис. 1, а.
Требуется:
1) Построить эпюру крутящих моментов;
2) Найти допускаемую величину момента М;
3) Построить эпюры касательных напряжений по сечениям вала, отметив на сечениях опасные точки;
4) Построить эпюру углов закручивания;
Модуль упругости при сдвиге материала вала G = 8×107 кН/м2. Расчетное сопротивление материала вала срезу RC = 105 кН/м2.
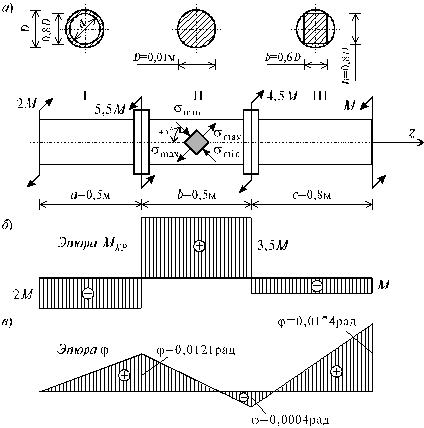
Рис.1
Решение.
1. Построить
эпюру крутящих моментов. Для определения величины крутящих моментов
используется метод сечений. Согласно расчетной схемы (рис. 2, а) для I участка (![]() ):
):
![]() откуда
откуда ![]() .
.
Согласно
расчетной схемы (рис. 2, б)
для участка II (![]() ):
):
![]() откуда
откуда ![]() .
.
Согласно
расчетной схемы (рис. 2, в)
для участка III (![]() ):
):
![]() откуда
откуда ![]() .
.
По полученным данным строим эпюру крутящих моментов (рис. 1, б).
2. Найти допускаемую величину момента М. Допускаемая величина момента МP определяется из условия прочности:
![]() .
.
Сначала определим моменты сопротивления сечения валика для каждого участка.
I участок
(трубчатое сечение) :
![]() где
где ![]() ;
;
![]() м3.
м3.
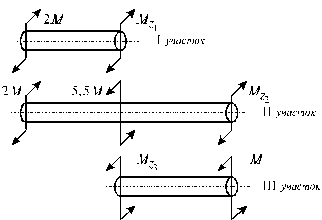
Рис.2
II участок
(круглое сечение):
![]() м3.
м3.
III участок
(прямоугольное сечение):
![]() ,
,
где ![]() - коэффициент, зависящий от отношения сторон
прямоугольного сечения h/b (h > b). В данном случае
- коэффициент, зависящий от отношения сторон
прямоугольного сечения h/b (h > b). В данном случае ![]() ,
, ![]() тогда
тогда
![]() м3.
м3.
Подсчитаем теперь напряжения по участкам в зависимости от момента М:
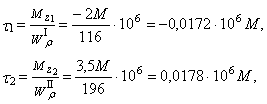
![]() .
.
Из сравнения результатов видно, что наиболее напряженным является участок II, поэтому допускаемая величина момента [M] определяется из зависимости:
![]()
откуда
![]() кН×м.
кН×м.
4. Построить эпюры касательных напряжений по сечениям вала, отметив на сечениях опасные точки. Касательные напряжения в точках поперечного сечения валика определяются по формулам:
для круглого
сечения при ![]() ,
, 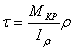 ;
;
для трубчатого
сечения при ![]() ,
, 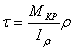 ;
;
для
прямоугольного сечения ![]() (в середине большей
стороны) и
(в середине большей
стороны) и ![]() (в середине меньшей
стороны).
(в середине меньшей
стороны).
Подсчитаем моменты инерции сечений валика относительно центра их кручения.
Участок I
(трубчатое сечение):
![]() м4.
м4.
Участок II
(круглое сечение):
![]() м4.
м4.
Участок III
(прямоугольное сечение):
![]() м4,
м4,
где ![]() = 0,243 при h/b = 1/33.
= 0,243 при h/b = 1/33.
Определим значения напряжений в характерных точках сечений.
Участок I (![]() ):
):
при ![]()
при ![]() .
.
Участок II (![]() ):
):
при ![]()
при ![]() .
.
Участок III (![]() ):
):
в середине большей стороны
![]()
в середине меньшей стороны
![]() МПа.
МПа.
где ![]() = 0,906 при h/b = 1,33.
= 0,906 при h/b = 1,33.
По полученным данным строятся эпюры напряжений, приведенные на рис. 3.
4. Построить эпюру углов закручивания. Угол закручивания на i-ом участке вала определяется:
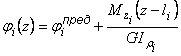 ,
,
где![]() - угол
закручивания на правом конце (i-1)-го
участка (для первого участка
- угол
закручивания на правом конце (i-1)-го
участка (для первого участка ![]() - начальный
угол закручивания вала); li
-
координата начала i-го
участка.
- начальный
угол закручивания вала); li
-
координата начала i-го
участка.

Рис.3
Так как, в
данном случае в пределах каждого из трех участков крутящие моменты и жесткости
на кручение ![]() постоянны, то эпюры
углов закручивания на каждом из участков будут линейны. В связи с этим,
достаточно подсчитать их значения лишь на границах участков. Приняв, что левый
конец вала защемлен от поворота, т.е.
постоянны, то эпюры
углов закручивания на каждом из участков будут линейны. В связи с этим,
достаточно подсчитать их значения лишь на границах участков. Приняв, что левый
конец вала защемлен от поворота, т.е. ![]() , получим:
, получим:
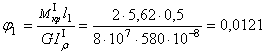 рад;
рад;
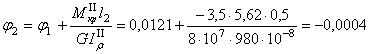 рад;
рад;
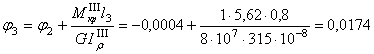 рад.
рад.
По полученным
данным строим эпюру углов закручивания ![]() (рис. 1, в). Сравнивая эпюры
(рис. 1, в). Сравнивая эпюры ![]() и
и ![]() , можно
отметить очевидную закономерность их изменения по оси z, вытекающую из расчетных формул.
, можно
отметить очевидную закономерность их изменения по оси z, вытекающую из расчетных формул.
Пример
№ 23
Для заданного
вала, находящегося в равновесии и нагруженного, как показано на рисунке,
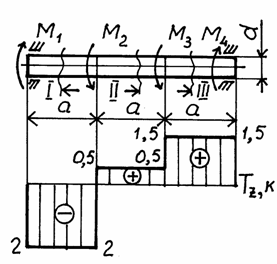
построить эпюру крутящих моментов, если М1 =2000 Нм =200 кгм, М2=2500 Нм =250 кгм,
М3=1000 Нм =100 кгм, М4=1500 Нм
=150 кгм, а
= 1 м.
Решение.
Вспомним
правило знаков: внутренний крутящий момент Мz в произвольном сечении бруса
положителен, если внешний крутящий момент стремится повернуть отсеченную часть
вала против часовой стрелки, если смотреть со стороны сечения.
Применим метод
сечения, учитывая, что внутренний крутящий момент в произвольном сечении бруса
численно равен алгебраической сумме внешних крутящих моментов, приложенных к
валу по одну сторону от этого сечения, т.е.:
![]() .
(1)
.
(1)
Разобьем вал
на три участка, проведем произвольные сечения I, II и III и стрелками укажем направление взгляда
на оставшуюся часть вала. Тогда, используя зависимость, получим:
участок АВ: ![]() = –200 кгм = –2·10-3 Нм;
= –200 кгм = –2·10-3 Нм;
участок ВС: ![]() = –100 + 150 = +50 кгм = 0,5·103 Нм;
= –100 + 150 = +50 кгм = 0,5·103 Нм;
участок СД: ![]() =150 кгм = 1,5·103 Нм.
=150 кгм = 1,5·103 Нм.
Выбираем
масштаб и строим эпюру Мz.
Для проверки используем правило: в сечениях вала, где приложены внешние
крутящие моменты, на эпюре Мz возникают скачки на величину этих моментов и в их направлении.
Пример
№ 24
Проверить
прочность стального вала, показанного на рисунке из предыдущего примера №23,
если его диаметр d
= 65 мм, а ![]() = 40 МПа.
= 40 МПа.
Решение.
Находим
опасное сечение (сечение, в котором ![]() ). Это любое поперечное
сечение на участке АВ, где
). Это любое поперечное
сечение на участке АВ, где ![]() = 200 кгм.
= 200 кгм.
Согласно
формуле условия прочности на кручение, получим:
![]() (1)
(1)
или
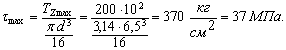
Прочность вала
обеспечена.
Пример
№ 25
К стальному
валу (G= 8·104
МПа = 8·105 кг/см2) приложен крутящий момент М = 7·103 Нм = 700 кгм (см.рис).
Требуется:
1. Установить,
при каком значении момента X угол поворота концевого
сечения вала равен нулю.
2. Построить
эпюру крутящих моментов с учетом найденного значения X.
3. Определить
диаметр вала, если ![]() = 80 МПа = 800 кг/см2.
= 80 МПа = 800 кг/см2.
4. Построить
эпюру углов закручивания.
5. Найти
наибольший относительный угол закручивания (на 1 м), если а =
2 м = 200 см, b
= 1,5 м = 150 см.
Решение.
1. Вал имеет
два участка АВ и ВС. Проводим сечения I и II и определяем для каждого участка
внутренний крутящий момент, начиная от свободного правого конца вала, чтобы не
определять реактивный момент в заделке. Используя зависимость, получим:
участок СВ: ![]() = –Х;
= –Х;
участок ВА: ![]() = –Х + М
= 700 – Х.
(1)
= –Х + М
= 700 – Х.
(1)
Угол
закручивания ![]() определяется по формуле:
определяется по формуле:
![]() .
(2)
.
(2)
Если вал имеет
n участков,
то угол закручивания его конечных сечений равен алгебраической сумме углов
закручивания каждого i-го участка,
т.е.
 .
(3)
.
(3)
Тогда,
учитывая условие рассматриваемого пункта о том, что угол поворота сечения С
относительно А равен нулю, запишем с учетом (2) и (3):
![]() ;
; ![]() ;
;
![]() .
.
Подставив из
(1) значения ![]() и
и ![]() , получим после преобразований:
, получим после преобразований:
![]() ; Х = 400 кгм.
; Х = 400 кгм.
2. Строим
эпюру крутящих моментов:
![]() = –Х = –400 кгм =
–4×103
Нм,
= –Х = –400 кгм =
–4×103
Нм,
![]() = –Х + М
= –400 + 700 = 300 кгм = 3×103 Нм.
= –Х + М
= –400 + 700 = 300 кгм = 3×103 Нм.
Выбираем масштаб
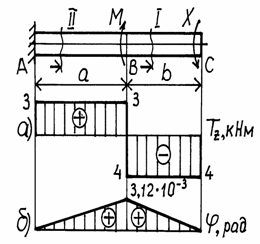
и строим эпюру Tz (рис. а).
3. Определяем
диаметр вала из расчета на прочность. Опасное сечение на участке СВ: ![]() =4·103 Нм = 400 кгм.
Определяем диаметр вала по формуле, полученной из условия прочности:
=4·103 Нм = 400 кгм.
Определяем диаметр вала по формуле, полученной из условия прочности:
![]() или
или ![]()
Согласно
стандартному ряду, округляем: d = 70 мм.
4. Строим
эпюру углов закручивания. Идем от неподвижного сечения вала А. Угол поворота
сечения В относительно сечения А, согласно формуле (2):
![]() рад;
рад;
![]() см4.
см4.
Аналогично: ![]() рад.
рад.
Выбираем
масштаб. На эпюре углов закручивания (рис. б)
под сечением В откладываем значение ![]() рад и соединяем
полученную точку с началом координат. Затем под сечением С откладываем
рад и соединяем
полученную точку с началом координат. Затем под сечением С откладываем ![]() = 3,12·10-3
– 3,12·10-3 = 0 и строим эпюру
= 3,12·10-3
– 3,12·10-3 = 0 и строим эпюру ![]() на участке СВ. Эпюра
на участке СВ. Эпюра ![]() в сечении С пришла в
ноль. Это говорит о том, что условие пункта 1 задачи выполнено и значение момента Х найдено правильно.
в сечении С пришла в
ноль. Это говорит о том, что условие пункта 1 задачи выполнено и значение момента Х найдено правильно.
5. Определяем
наибольший относительный угол закручивания ![]() . Для каждого участка получим, поделив угол закручивания на
его длину:
. Для каждого участка получим, поделив угол закручивания на
его длину:
![]() рад/м;
рад/м;
![]() рад/м;
рад/м;
Отсюда ![]() рад/м.
рад/м.
Пример
№ 26
К стальному
валу постоянного поперечного сечения (см. рис. а) приложены четыре внешних скручивающих
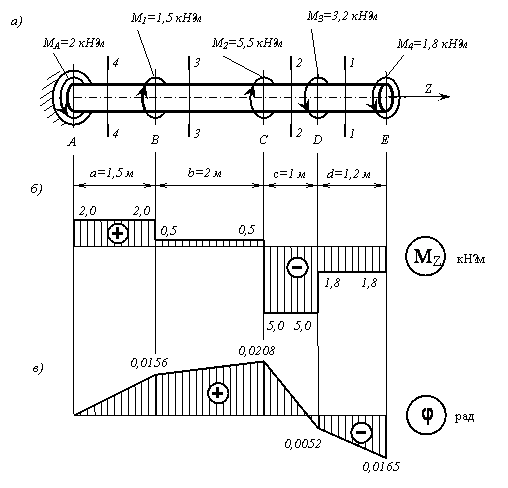
момента: ![]() кНм;
кНм;
![]() кНм;
кНм;
![]() кНм;
кНм;
![]() кНм.
Длины участков стержня:
кНм.
Длины участков стержня: ![]() м;
м; ![]() м,
м, ![]() м,
м, ![]() м.
м.
Требуется:
построить эпюру крутящих моментов, определить диаметр вала при ![]() кН/см2 и
построить эпюру углов закручивания поперечных сечений стержня.
кН/см2 и
построить эпюру углов закручивания поперечных сечений стержня.
Решение.
1. Определяем реактивный момент, возникающий в
жесткой заделке.
Обозначим
момент в заделке ![]() и направим его,
например, против хода часовой стрелки (при взгляде навстречу оси z).
и направим его,
например, против хода часовой стрелки (при взгляде навстречу оси z).
Запишем
уравнение равновесия вала. При этом будем пользоваться следующим правилом
знаков: внешние скручивающие моменты
(активные моменты, а также реактивный момент в заделке), вращающие вал против хода часовой стрелки (при взгляде на него
навстречу оси z), считаем положительными.
Тогда
![]()
![]() кНм.
кНм.
Знак «плюс» в
полученном нами выражении говорит о том, что мы угадали направление реактивного момента ![]() , возникающего в заделке.
, возникающего в заделке.
2. Строим
эпюру крутящих моментов.
Напомним, что внутренний крутящий момент Mz, возникающий в некотором поперечном сечении стержня, равен алгебраической сумме внешних скручивающих моментов,
приложенных к любой из рассматриваемых частей стержня (то есть действующих
левее или правее сделанного сечения). При этом внешний скручивающий момент, вращающий рассматриваемую часть
стержня против хода часовой стрелки (при взгляде на поперечное
сечение), входит в эту алгебраическую сумму со знаком «плюс», а по ходу
– со знаком «минус».
Соответственно, положительный внутренний
крутящий момент, противодействующий внешним скручивающим моментам,
направлен по ходу часовой стрелки (при взгляде на поперечное сечение),
а отрицательный – против ее хода.
Разбиваем
длину стержня на четыре участка (рис. а).
Границами участков являются те сечения, в которых приложены внешние моменты.
Делаем по
одному сечению в произвольном месте
каждого из четырех участков стержня.
Начнем с
сечения 1–1. Мысленно отбросим (или
закроем листком бумаги) левую часть стержня. Чтобы уравновесить скручивающий
момент ![]() кНм,
в поперечном сечении стержня должен возникнуть равный ему и противоположно
направленный крутящий момент
кНм,
в поперечном сечении стержня должен возникнуть равный ему и противоположно
направленный крутящий момент ![]() . С учетом упомянутого выше правила знаков
. С учетом упомянутого выше правила знаков
![]() кНм.
кНм.
По аналогии,
для сечений 2 – 2 и 3 – 3 находим:
![]() кНм;
кНм;
![]() кНм.
кНм.
Чтобы
определить крутящий момент, в сечении 4 –
4 отбросим правую часть стержня. Тогда
![]() кНм.
кНм.
Легко
убедиться в том, что полученный результат не изменится, если мы отбросим теперь
не правую, а левую часть стержня. Получим
![]() кНм.
кНм.
Для построения
эпюры крутящих моментов ![]() проводим тонкой линией ось, параллельную оси
стержня z (рис. б). Вычисленные значения крутящих
моментов в выбранном масштабе и с учетом их знака откладываем от этой оси. В
пределах каждого из участков стержня крутящий момент постоянен, поэтому мы как
бы «заштриховываем» вертикальными линиями соответствующий участок. Напомним,
что каждый отрезок «штриховки» (ордината эпюры) дает в принятом масштабе
значение крутящего момента в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
проводим тонкой линией ось, параллельную оси
стержня z (рис. б). Вычисленные значения крутящих
моментов в выбранном масштабе и с учетом их знака откладываем от этой оси. В
пределах каждого из участков стержня крутящий момент постоянен, поэтому мы как
бы «заштриховываем» вертикальными линиями соответствующий участок. Напомним,
что каждый отрезок «штриховки» (ордината эпюры) дает в принятом масштабе
значение крутящего момента в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Отметим, что в
местах приложения внешних скручивающих моментов на эпюре ![]() мы получили
скачкообразное изменение внутреннего
крутящего момента на величину соответствующего внешнего момента.
мы получили
скачкообразное изменение внутреннего
крутящего момента на величину соответствующего внешнего момента.
3. Определяем
диаметр вала из условия прочности.
Условие прочности при кручении имеет вид
![]() ,
,
где ![]() – полярный момент
сопротивления (момент сопротивления при кручении).
– полярный момент
сопротивления (момент сопротивления при кручении).
Наибольший по абсолютному значению крутящий момент возникает на втором участке
вала: ![]() кНсм.
кНсм.
Тогда требуемый диаметр вала определяется по
формуле
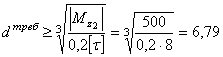 см.
см.
Округляя полученное значение до стандартного,
принимаем диаметр вала равным ![]() мм.
мм.
4. Определяем углы закручивания поперечных
сечений A, B, C, D и E и строим эпюру углов
закручивания.
Сначала вычисляем крутильную жесткость
стержня ![]() , где G – модуль сдвига, а
, где G – модуль сдвига, а ![]() – полярный момент
инерции. Получим
– полярный момент
инерции. Получим
![]() кНсм2.
кНсм2.
Углы
закручивания на отдельных участках стержня равны:
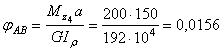 рад;
рад;
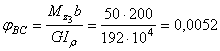 рад;
рад;
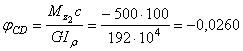 рад;
рад;
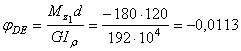 рад.
рад.
Угол закручивания в заделки равен нулю, то
есть ![]() . Тогда
. Тогда
![]() рад;
рад;
![]() рад;
рад;
![]() рад;
рад;
![]() рад.
рад.
Эпюра углов закручивания показана на рисунке
в. Отметим, что в пределах длины
каждого из участков вала угол закручивания изменяется по линейному закону.
Пример
№ 27
Построить эпюры крутящих моментов ![]() и угловых перемещений
и угловых перемещений ![]() , произвести расчеты на прочность и жесткость (см. рис.).
, произвести расчеты на прочность и жесткость (см. рис.).
|
а) в) г) |
б) метод сечений |
Решение.
1. Уравнения
равновесия
Вычисляем
сумму всех внешних моментов, действующих на стержень, круглого поперечного сечения и приравниваем
ее к нулю
![]() .
.
С учетом ![]() получим реактивный
момент в заделке
получим реактивный
момент в заделке
![]() .
.
2. Определение
выражений крутящих моментов методом сечений и построение эпюры ![]() .
.
Стержень имеет
два участка, на которых выражения крутящих моментов различны. Рассекаем
стержень на первом и втором участках и рассматриваем в каждом из этих случаев
одну из отсеченных частей (рис. б).
Для первого участка (![]() )
)
![]() ,
,
для второго (![]() )
)
![]() .
.
Строим эпюру
крутящих моментов. На первом участке откладываем отрицательное постоянное
значение ![]() . На втором участке эпюра – прямая линия. Для ее построения
достаточно иметь две точки: при
. На втором участке эпюра – прямая линия. Для ее построения
достаточно иметь две точки: при ![]() и
и ![]() . Соответствующие моменты
. Соответствующие моменты ![]() и
и ![]() . Наносим на график эти точки и проводим прямую линию (рис. в). В сечениях, где действуют
сосредоточенные моменты, имеют место скачки, равные по величине значениям этих
моментов. Наибольший момент возникает в сечении
. Наносим на график эти точки и проводим прямую линию (рис. в). В сечениях, где действуют
сосредоточенные моменты, имеют место скачки, равные по величине значениям этих
моментов. Наибольший момент возникает в сечении ![]() :
:
![]() .
.
3. Контроль
правильности построенной эпюры с помощью дифференциальной зависимости Д.
Журавского
![]() ,
,
позволяющей
установить следующие правила:
- на
незагруженном участке ![]() эпюра
эпюра ![]() постоянна;
постоянна;
- на
равномерно загруженном участке ![]() эпюра − прямая
линия
эпюра − прямая
линия ![]() , возрастающая с ростом
, возрастающая с ростом ![]() , если
, если ![]() , и убывающая, если
, и убывающая, если ![]() ;
;
- в сечениях,
где действует сосредоточенный момент, имеет место скачок на величину этого
момента.
В нашем
примере все правила контроля выполняются.
4. Расчет на
прочность при кручении бруса
Условие
прочности при кручении
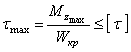 .
.
Так как ![]() , то получаем
, то получаем
![]() .
.
Если ![]() известны, то находим
допустимое значение момента
известны, то находим
допустимое значение момента
![]() .
.
При
проектировочном расчете находим размер поперечного сечения, т.е. диаметр
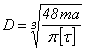 .
.
В этом случае
должны быть известны ![]() .
.
Третий тип
расчета – проверочный.
5. Построение
эпюры угловых перемещений ![]() (рис. г)
(рис. г)
Угловые
перемещения находим по формуле
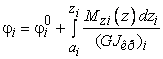 ,
,
где ![]() − номер участка,
− номер участка,
![]() − значение угла в начале
− значение угла в начале ![]() -го участка,
-го участка, ![]() − крутящий
момент на
− крутящий
момент на ![]() -м участке,
-м участке, ![]() − координата
начала
− координата
начала ![]() -го участка,
-го участка, ![]() − жесткость при
кручении на i-м
участке.
− жесткость при
кручении на i-м
участке.
На первом
участке ![]() (защемление).
(защемление).
Угол поворота
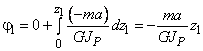 .
.
Эпюра – прямая
линия. При ![]() , при
, при ![]() получим
получим 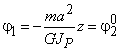 .
.
На втором
участке
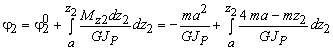 ,
,
или
![]() .
.
График-эпюра ![]() − квадратичная
парабола.
− квадратичная
парабола.
При ![]() получаем
получаем 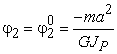 , при
, при ![]() −
− 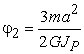 .
.
Выпуклость
параболы определяется знаком второй производной. Производные
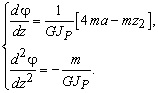
Так как в
задаче ![]() , то
, то ![]() и выпуклость эпюры
обращена кверху. Первая производная обращается в нуль при
и выпуклость эпюры
обращена кверху. Первая производная обращается в нуль при ![]() , что за пределами стержня, поэтому эпюра
, что за пределами стержня, поэтому эпюра ![]() не имеет экстремума.
не имеет экстремума.
Помимо условия
прочности иногда проверяется условие жесткости при кручении
![]() ,
,
где ![]() − относительный
угол закручивания,
− относительный
угол закручивания, ![]() − допускаемое
значение относительного угла закручивания.
− допускаемое
значение относительного угла закручивания.
Пример
№ 28
Дано: Т1=50
кНм; l1=3,6 м; l2=2,6 м; l3=1,8 м; ![]() =100 МПа
=100 МПа
Требуется:
1. Подобрать
диаметр сплошного и полого вала
2. Построить
эпюру углов закручивания.
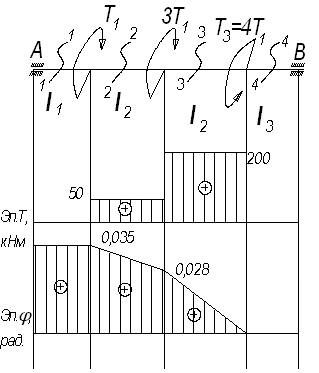
Решение.
Рассмотрим
сечение 1-1:
Т1-1=0;
Рассмотрим
сечение 2-2: Т2-2=Т1=50 кНм
Сечение 3-3:
Т3-3=Т1+3Т1=50+150=200
кНм
Сечение 4-4:
Т4-4=0
ТМАХ=200 кНм
Диаметр
сечения сплошного вала
![]()
Принимаем d=220мм
Диаметр
сечения полого вала
![]()
Принимаем D=230мм, d=115мм
Определим на
сколько полый вал легче сплошного

Построим эпюру
углов закручивания, производя расчет от ведущего шкива
![]()
![]()
![]()
![]()
Онлайн-калькулятор "Подбор диаметра вала при кручении"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов