Главная
Лекция 6 (продолжение). Примеры решения на плоский изгиб
Определение перемещений при изгибе методом начальных параметров
Пример 1.
1) Однопролетная балка находится под действием сосредоточенной силы Р (рис. а).
2) Однопролетная балка находится под действием сосредоточенного момента в опоре (рис. б).
Для обеих балок найти дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота методом начальных параметров.
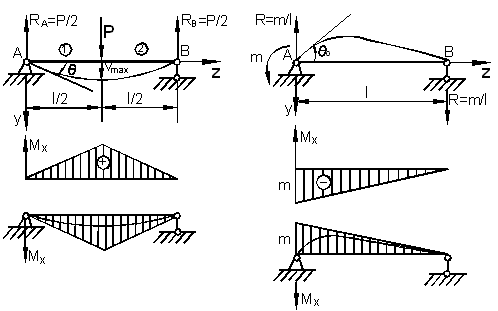
а)
б)
Решение.
1) Опорные реакции ![]() . Балка имеет два участка с различными выражениями для
изгибающих моментов:
. Балка имеет два участка с различными выражениями для
изгибающих моментов:
![]() (1)
(1)
В этом случае дифференциальные уравнения изгиба на каждом из участков имеют различный вид:
![]() (2)
(2)
Интегрирование этих уравнений приведет к выражениям для прогибов v1, v2, которые будут содержать четыре постоянные интегрирования. Для их определения нужно составить четыре граничных условия. Это вызовет определенные трудности при решении данной задачи. Метод начальных параметров существенно упрощает решение задачи по определению прогибов балки.
Составим выражения прогибов для каждого из участков, пользуясь формулой:
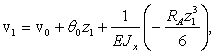 (3)
(3)
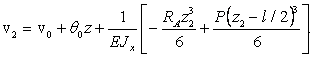 (4)
(4)
Начальные параметры определяем из граничных условий:
![]() (5)
(5)
Подставляя ![]() в (3) и
в (3) и ![]() в (4), согласно (5), находим:
в (4), согласно (5), находим:
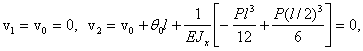 (6)
(6)
откуда получаем:
![]() (7)
(7)
Подставляя
значения![]() в (3), (4), получим выражения прогибов на каждом из двух
участков. Максимальный прогиб находим из (3) либо (4) при
в (3), (4), получим выражения прогибов на каждом из двух
участков. Максимальный прогиб находим из (3) либо (4) при
![]() . В результате вычислений находим:
. В результате вычислений находим:
![]() (8)
(8)
Угол поворота на втором участке:
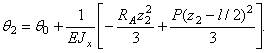
На правой опоре В при z =l получаем:
![]()
2) В данном примере опорные реакции ![]() Прогибы балки в произвольном
сечении:
Прогибы балки в произвольном
сечении:
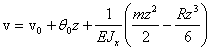 (1)
(1)
или, с учетом ![]() ,
,
![]() (2)
(2)
Угол поворота находим дифференцированием (2):
![]() (3)
(3)
При z = 0 на
левой опоре А имеем v = 0, что позволяет найти ![]()
На правой
опоре В при z = ![]() прогиб v = 0, т.е.
прогиб v = 0, т.е.
![]()
откуда
![]() (4)
(4)
На опоре В при z = ![]() угол поворота,
согласно (3), равен:
угол поворота,
согласно (3), равен:
![]() (5)
(5)
Пример 2.
Однопролётная балка
с консолью находится под действием распределённой нагрузки ![]() (см. рис.). Найти дифференциальное уравнение
изгиба и найти максимальные прогибы и углы поворота методом начальных
параметров.
(см. рис.). Найти дифференциальное уравнение
изгиба и найти максимальные прогибы и углы поворота методом начальных
параметров.
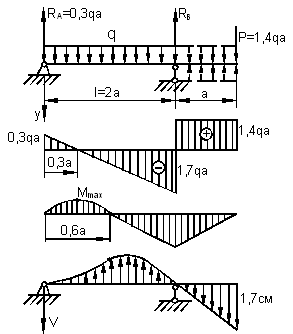
Решение.
Определим
прогибы в середине пролета балки и на конце ее консольной части. Составим
уравнения равновесия:
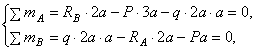
откуда
![]()
![]()
Для статической проверки правильности найденных значений реакции составляем третье уравнение - сумму проекций на вертикальную ось у:
![]()
или
![]()
Следовательно, реакции найдены верно.
На опорах балки при z = 0, z = 2а имеем v = 0.
Находим
![]()
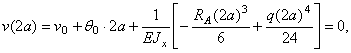
откуда следует:
![]()
![]()
Искомые перемещения:
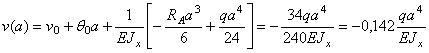

Если принять ![]() а = 2 м, то получим
а = 2 м, то получим
![]()
![]()
При вычислении
прогиба ![]() на конце консольной части распределенная нагрузка не доходит
до рассматриваемого сечения, что является обязательным при применении универсального
уравнения. Чтобы выйти из положения, распределенную нагрузку продолжаем до
рассматриваемого сечения и добавляем такую же, но противоположного направления
(см. рис.). Добавление такой же нагрузки в результате дает нагрузку,
статически эквивалентную нулю, что не вызовет изменений в деформированном
состоянии балки.
на конце консольной части распределенная нагрузка не доходит
до рассматриваемого сечения, что является обязательным при применении универсального
уравнения. Чтобы выйти из положения, распределенную нагрузку продолжаем до
рассматриваемого сечения и добавляем такую же, но противоположного направления
(см. рис.). Добавление такой же нагрузки в результате дает нагрузку,
статически эквивалентную нулю, что не вызовет изменений в деформированном
состоянии балки.
Построим
изогнутую ось балки. Для этого отложим на рисунке значения найденных прогибов с
учетом их знаков. Кроме того, необходимо вспомнить, что выпуклость эпюры моментов
от распределенной нагрузки совпадает с выпуклостью кривой изогнутой оси. В
точке, где ![]() имеет место смена
кривизны изогнутой оси балки. Сечение, в котором
имеет место смена
кривизны изогнутой оси балки. Сечение, в котором![]() найдем из условия
найдем из условия
![]()
откуда ![]() Эпюра прогибов изображена на рисунке.
Эпюра прогибов изображена на рисунке.
Пример 3.
Элемент машины представляет собой балку пролетом 3a, опирающуюся на шарнирно подвижную опору, а с другой – на вертикальные направляющие, вдоль которых свободно (без трения) скользит ползун, жесткосвязанный с балкой. Определить прогибы в точках А и С и угол поворота на опоре В.

Решение.
1. Определение опорных реакций. Составляем уравнения равновесия и находим искомые реакции:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Определение
начальных параметров. Из условий опирания балки имеем ![]() =
0 и
VВ
= 0. Из первого получаем
=
0 и
VВ
= 0. Из первого получаем ![]() = 0, а из второго
находим Vо:
= 0, а из второго
находим Vо:
![]() ,
, ![]() .
.
3. Определение искомых перемещений. Имеем
![]() ;
; ![]() ,
,
![]() .
.
Пример 4.
Определить углы поворота опорных сечений и прогибы на конце консоли и в середине пролета. Построить пунктиром вид изогнутой оси балки.
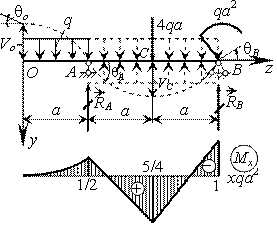
Решение.
1. Определение опорных реакций. Из уравнений равновесия имеем
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
2. Определение начальных параметров. Из условий опирания балки VA = VB = 0 или в развернутом виде
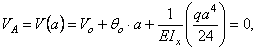
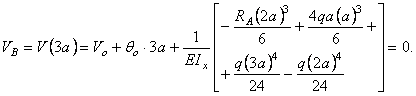
Таким образом, получаем систему
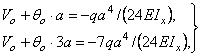
откуда ![]() ,
, ![]() .
.
3. Определение
искомых перемещений. Угол поворота на
опоре А
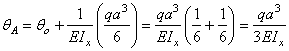 .
.
Угол поворота
на опоре В
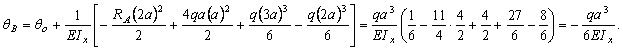
Прогиб посредине пролета (сеч. С)
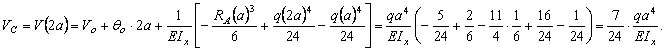
Примерный вид упругой линии
балки показан на рисунке пунктиром.
Пример 5.
Определить место и значение
наибольшего прогиба, а также углы поворота опорных сечений двухопорной балки
постоянной жесткости, нагруженной сосредоточенными моментами.

Решение.
1. Определение опорных реакций.
Имеем ![]() , RA
, RA![]() a = 3M,
RA = RB = M/a.
a = 3M,
RA = RB = M/a.
2. Определение
начальных параметров. Из условий опирания балки
VA
= VB
= 0. Согласно первому условию Vо = 0, а
из второго находим ![]() :
:
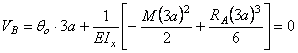 ,
,
откуда ![]() .
.
Следовательно, уравнения прогибов и углов поворота имеют вид
![]() ,
, ![]() .
.
Наибольший
прогиб возникает в том сечении, где dv/dz
= ![]() = 0, т.е. при z = 2a.
Подставив в уравнение прогибов z = 2a, вычислим наибольший прогиб
= 0, т.е. при z = 2a.
Подставив в уравнение прогибов z = 2a, вычислим наибольший прогиб
Vmax = -2Ma2/(3EIx).
Интересно отметить, что прогиб посредине пролета балки равен Vср = V(1,5a) = -9Ma2/(16EIx) и отличается от наибольшего на 15%.
Угол поворота сечения В
![]() =
= ![]() (3a)
= 3Ma/(2EIx).
(3a)
= 3Ma/(2EIx).
Пример 6.
Определить максимальный прогиб однопролетной балки, изображенной на рисунке. Жесткость балки на изгиб постоянна и равна EI.
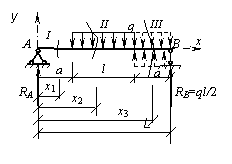
Решение.
Определяем опорные реакции RA, RB. С учетом симметрии находим RA = RB = ql/2.
Мысленно проводим сечения в каждом из трех участков рассматриваемой балки. Сечения имеют абсциссы х1, х2 и х3, так как начало координат помещено в точке А.
Запишем значения изгибающих моментов в каждом из проведенных сечений:
![]()
![]()
![]()
При определении МIII учитывалось, что распределенную нагрузку q необходимо продолжить вправо на всю длину балки, а на третьем участке необходимо ввести компенсирующую нагрузку, противоположную по направлению заданной и с той же интенсивностью q. Проведенная операция с распределенной нагрузкой q не влияет на напряженно-деформированное состояние балки, но дает преимущества при вычислении произвольных постоянных С и D.
Интегрируем
полученные выражения согласно формуле ![]() :
:
![]()
![]()
![]() (1)
(1)
Интегрируя еще раз полученные зависимости, получаем значения прогибов для каждого участка балки:
![]()
![]()
![]() (2)
(2)
Для определения постоянных интегрирования С и D необходимо поставить два граничных условия. Рассматривая балку на рисунке, замечаем, что прогибы на опорах А и В равны нулю, так как шарнирно подвижная В и шарнирно неподвижная А опоры препятствуют вертикальному перемещению концов балки. Следовательно, граничные условия можно записать как: при х1 = 0 имеем уI = 0 и при х3 = 2a + l имеем уIII = 0.
Применительно к формулам (2) получаем, что при x1 = 0 имеем yI = =D = 0, откуда D = 0, а при x3 = 2a + l имеем
![]()
откуда, принимая 2a + l = L, находим:
![]()
Подставляя полученное выражение для C и D = 0 в формулы (2), определяем
![]()
![]()
![]()
Подставляя выражение для определения С и равенство D = 0 в формулы (1), получим формулы для вычисления углов поворота поперечных сечений балки для каждого участка.
По условию задачи требуется определить максимальный прогиб балки. С учетом симметрии балки (см. рис.) делаем вывод, что уmax будет посередине второго участка или что то же самое в середине пролета балки. Для вычисления уmax используем формулу для прогибов второго участка при x2 = L/2 или x2 = a + l/2:
![]()
Полагая a = 0, l = L из полученной формулы можно получить максимальный прогиб в
середине пролета балки, полностью загруженной равномерно распределенной
нагрузкой q
![]()
Подставляя
значение x2 = L/2 или x2
= a + l/2,
находим угол поворота поперечного сечения в середине второго участка ![]() (x = L/2) = 0.
(x = L/2) = 0.
Пример 7.
Для балки, показанной на рис. а, требуется найти прогиб в сечении С, угол поворота в сечении В аналитическим способом и проверить условие жесткости, если допускаемый прогиб равен l/200. Балка выполнена из дерева и имеет поперечное сечение из трех бревен радиусом 12 см. (Подбор сечения этой балки см. выше)

Решение.
Для
определения перемещений балки аналитическим способом составим дифференциальное
уравнение изогнутой оси ![]() , используя правила Клебша записи выражения для
изгибающего момента. Начало координат в рассматриваемой задаче рациональнее
выбрать справа (в заделке). Распределенную нагрузку
, используя правила Клебша записи выражения для
изгибающего момента. Начало координат в рассматриваемой задаче рациональнее
выбрать справа (в заделке). Распределенную нагрузку ![]() , которая не доходит до левого конца балки, продлим до
сечения С
(рис. в). Выражение для изгибающего
момента будет иметь такой вид:
, которая не доходит до левого конца балки, продлим до
сечения С
(рис. в). Выражение для изгибающего
момента будет иметь такой вид:

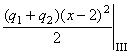 .
.
Подставим это
выражение в дифференциальное уравнение ![]() и проинтегрируем его
два раза:
и проинтегрируем его
два раза:
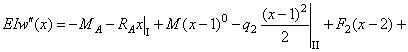
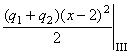 ;
;
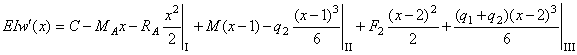 ;
;
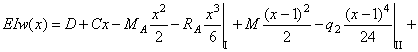
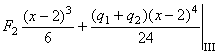 .
.
Для определения постоянных С и D запишем граничные условия: в заделке (в сечении А, где находится начало координат) угол поворота и прогиб балки равны нулю, то есть
![]() и
и ![]() .
.
Подставляя эти условия в выражения для угла поворота и прогиба на первом участке, найдем, что
![]() и
и ![]() .
.
Теперь можно
определить заданные перемещения. Для определения угла поворота в сечении В подставим в выражение для угла
поворота на первом участке (только до черты с номером I) значение ![]() :
:
![]() кНм2.
кНм2.
В соответствии с правилом знаков отрицательный знак угла поворота для выбранного начала координат х справа означает, что поворот сечения происходит по часовой стрелке.
В сечении С, где требуется найти прогиб,
координата х равна ![]() , и
это сечение находится на третьем участке балки, поэтому подставляем х = 4 м в выражение для прогибов,
используя слагаемые на всех трех участках:
, и
это сечение находится на третьем участке балки, поэтому подставляем х = 4 м в выражение для прогибов,
используя слагаемые на всех трех участках:
![]()
![]() кНм3.
кНм3.
Знак минус у найденного прогиба показывает, что сечение С перемещается вверх. Покажем найденные перемещения на изогнутой оси балки. Чтобы нарисовать ось балки после деформации, построим эпюру изгибающих моментов (рис. б). Положительный знак эпюры М на участке показывает, что балка на этом участке изгибается выпуклостью вниз, при отрицательном знаке М изогнутая ось имеет выпуклость вверх. Кроме того, деформированная ось балки должна удовлетворять условиям закрепления: в нашем случае на правом конце балка имеет жесткое защемление, и, как уже отмечалось при записи граничных условий, прогиб и угол поворота в защемлении должны равняться нулю. На рис. г изображена ось рассматриваемой балки после деформации, удовлетворяющая этим условиям. На изогнутой оси показаны найденные прогиб в сечении С и угол поворота сечения В с учетом их знаков.
В заключение сосчитаем прогиб балки в сантиметрах, угол поворота в радианах и проверим условие жесткости. Найдем жесткость ЕI рассматриваемой деревянной балки из трех бревен радиусом 12 см. Момент инерции поперечного сечения
![]() см4.
см4.
Модуль упругости дерева Е = 104 МПа = 103 кН/см2. Тогда
![]() кНсм2.
кНсм2.
Прогиб балки в сечении С
![]() см,
см,
а угол
поворота сечения В
![]() рад.
рад.
Очевидно (см.
рис. г), что найденный прогиб
балки в сечении С является максимальным,
поэтому для проверки условия жесткости сравним его с допускаемым прогибом. Для
балки длиной ![]() м
допускаемый прогиб согласно условию
м
допускаемый прогиб согласно условию ![]() см. Таким
образом, максимальный прогиб
см. Таким
образом, максимальный прогиб ![]() см меньше
допускаемого, и условие жесткости выполняется.
см меньше
допускаемого, и условие жесткости выполняется.
Пример 8.
В балке с двумя консолями, показанной на рис. а надо найти угол поворота сечения А и прогиб сечения D, используя аналитический способ. Сечение балки – двутавр № 24.

Решение.
Выберем начало отсчета координаты х на левом конце балки в точке А и запишем выражение для изгибающего момента на всех участках с учетом правил Клебша:
![]() .
.
Подставим это
выражение в дифференциальное уравнение изогнутой оси ![]() и проинтегрируем его
дважды:
и проинтегрируем его
дважды:
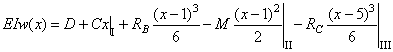 .
.
Найдем произвольные постоянные С и D из граничных условий. В точках В и С, где находятся опоры, прогибы не возможны. Поэтому
![]() ,
,
![]() .
.
Получили
систему из двух уравнений с двумя неизвестными С и D. Решая эту систему,
найдем С = 40 кНм2, D = – 40 кНм3. Проанализируем результат, используя
геометрический смысл произвольных постоянных С и D. На рис. в показана изогнутая ось балки, соответствующая
эпюре изгибающих моментов и условиям закрепления. Точка А, находящаяся в начале
координат, перемещается вверх, и поэтому следует ожидать, что ![]() будет иметь в
соответствии с правилом знаков отрицательный знак. Сечение в точке А поворачивается
по часовой стрелке, поэтому постоянная
будет иметь в
соответствии с правилом знаков отрицательный знак. Сечение в точке А поворачивается
по часовой стрелке, поэтому постоянная ![]() должна быть
положительна. Полученные знаки С и D не противоречат проведенному анализу.
должна быть
положительна. Полученные знаки С и D не противоречат проведенному анализу.
Теперь можно
найти искомые перемещения. Угол поворота сечения А определим, подставив в
выражение для ![]() на первом участке
значение х = 0, то есть
на первом участке
значение х = 0, то есть
![]() кНм2.
кНм2.
Чтобы найти
прогиб в точке D, в выражение для
прогибов ![]() подставляем
подставляем ![]() м,
используя все слагаемые этого выражения, так как точка находится на последнем
третьем участке:
м,
используя все слагаемые этого выражения, так как точка находится на последнем
третьем участке:
![]() кНм3.
кНм3.
Разделим полученные результаты на жесткость балки, чтобы сосчитать угол поворота в радианах, а прогиб в сантиметрах. Жесткость стальной двутавровой балки № 24:
![]() кНсм2.
кНсм2.
Угол поворота
сечения А
![]() рад.
рад.
Прогиб точки D
![]() см.
см.
Положительные знаки полученных перемещений свидетельствуют о том, что поворот сечения А происходит по часовой стрелке, а точка D перемещается вниз. Изогнутая ось балки с найденными перемещениями и точкой перегиба показана на рис. в.
Пример 9.
Для схем
стальных балок I и II, изображенных на рис. 1 и 2, определить методом
начальных параметров углы поворота сечения и прогиб в точке D. Модуль упругости Е = 2![]() кН/м2.
Поперечные сечения балок: схема I - круглое диаметром d = 0,24 м, схема
II - квадратное
со стороной a = 0,2 м.
кН/м2.
Поперечные сечения балок: схема I - круглое диаметром d = 0,24 м, схема
II - квадратное
со стороной a = 0,2 м.
Решение.
Схема
I.
1. Определение опорных реакций балки (рис. 1)
![]() ,
R0 + q×c - P = 0, R0 = -q×c + P = -10×1,4 + 12 = -2 кН;
,
R0 + q×c - P = 0, R0 = -q×c + P = -10×1,4 + 12 = -2 кН;
![]() ,
, ![]() ,
,
M0 = q c (b + 0,5 c) - M - P (b + c + e) = 10×1,4×(1,8 + 0,5×1,4) - 20 - 12×(1,8 + 1,4 + 1,2) = -37,8 кНм.
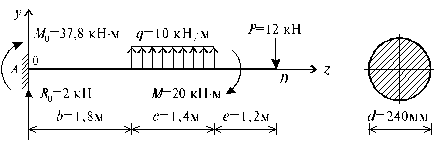
Рис. 1
Для проверки правильности определения опорных реакций составим уравнения равновесия:
![]() , M0 + R0×4,4 + q×c×(0,5×c + e) + M = -37,8 - 2×4,4 + 10×1,44×(0,5×1,4 + 1,2) + 20 = 46,6 - 46,6 = 0.
, M0 + R0×4,4 + q×c×(0,5×c + e) + M = -37,8 - 2×4,4 + 10×1,44×(0,5×1,4 + 1,2) + 20 = 46,6 - 46,6 = 0.
Реакции найдены верно.
2. Применение метода начальных параметров. Используя уравнение
![]()
для нашего случая запишем:
![]()
Здесь M0 и Q0 - момент и реакция в заделке (т.е. в начале координат).
Знак ![]() означает, что слагаемое, после которого он стоит, нужно
учитывать при z > b и не надо - при
означает, что слагаемое, после которого он стоит, нужно
учитывать при z > b и не надо - при ![]() . Начальные параметры имеют значения: y0 = 0;
. Начальные параметры имеют значения: y0 = 0; ![]() = 0; M0 = -37,8
кНм, R0 = -2 кН
(знак реакций определяется по знаку перемещения вызванного этими усилиями).
Тогда выражение для определения прогибов будет иметь вид:
= 0; M0 = -37,8
кНм, R0 = -2 кН
(знак реакций определяется по знаку перемещения вызванного этими усилиями).
Тогда выражение для определения прогибов будет иметь вид:
![]()
Соответственно выражение для определения углов поворота будет:
![]()
С помощью этих
выражений определяем ![]() и
и ![]() :
:
![]() кНм3.
кНм3.
![]() кНм2.
кНм2.
Жесткость
сечения при Е = 2![]() кН/м2
равна:
кН/м2
равна:
![]() кНм2.
кНм2.
Тогда, окончательно:
![]() м;
м;
![]() рад.
рад.
Прогиб точки D происходит вниз, а сечение поворачивается по часовой стрелке.
Схема
II.

Рис. 2
1. Определение опорных реакций балки (рис. 2).
![]() , RB ×(b + c + e) - q×(c + e)×[b + 0,5×(c + e)] + M + P×b = 0,
, RB ×(b + c + e) - q×(c + e)×[b + 0,5×(c + e)] + M + P×b = 0,
![]() кН;
кН;
![]() , R0×(b + c + e) - 0,5×q×(c + e)2 - M + P×(c + e) = 0,
, R0×(b + c + e) - 0,5×q×(c + e)2 - M + P×(c + e) = 0,
![]() кН.
кН.
Для проверки правильности определения опорных реакций составим уравнение равновесия сил по оси y:
![]() ; R0 + RB + P - q×(c + e) = 7,86 + 14,14 + 8 - 10×3 = 30 - 30 = 0.
; R0 + RB + P - q×(c + e) = 7,86 + 14,14 + 8 - 10×3 = 30 - 30 = 0.
Реакции найдены верно.
2. Применение метода начальных параметров. Используя метод начальных параметров, для рассматриваемой балки запишем:
![]()
Из условий
закрепления балки при z = 0
имеем: y0 = 0; М0=0.
Подставляя числовые значения, получим:
![]() .
.
В данном
выражении неизвестно ![]() . Из условия закрепления балки при z = b + c + e имеем, что y = 0.
Вычисляя прогиб на правом конце балки и приравнивая его к нулю, получим
уравнение для определения
. Из условия закрепления балки при z = b + c + e имеем, что y = 0.
Вычисляя прогиб на правом конце балки и приравнивая его к нулю, получим
уравнение для определения ![]() :
:
![]() .
.
Отсюда ![]() = -20,84 кНм2. Теперь выражение для определения прогибов
будет иметь вид:
= -20,84 кНм2. Теперь выражение для определения прогибов
будет иметь вид:
![]() .
.
Соответственно, выражение для определения углов поворота будет:
![]() .
.
С помощью этих
выражений определяем ![]() и
и ![]() :
:
![]() кHм3.
кHм3.
![]() кНм2.
кНм2.
Вычисляем
жесткость сечения (Е = 2![]() кН/м2):
кН/м2):
![]() кНм2.
кНм2.
Тогда, окончательно,
![]() м;
м; ![]() рад.
рад.
Перемещение точки D происходит вниз, а сечение поворачивается по часовой стрелке.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов


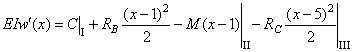 ;
;