Главная
Лекция 4. Геометрические характеристики плоских сечений
Содержание
Моменты инерции плоских сечений
простой формы
Моменты инерции простых сечений
Моменты инерции сечений сложной
формы
Изменение моментов инерции
сечения при повороте осей координат
Главные оси инерции и главные моменты
инерции
Понятие о радиусе и эллипсе инерции
сечения
Алгоритм расчета
геометрических характеристик плоских сечений
Сопротивление стержня различным видам деформирования часто зависит не
только от его материала и размеров, но и от характера осевой линии, формы
поперечных сечений и их ориентации.
Уже в древности строители знали, что доска или брус, поставленные на ребро, во много раз лучше противостоят изгибу, чем положенные плашмя. Речь идет как об их несущей способности, так и о деформативности. Для двутавровой стандартной балки, поставленной на две опоры, эти показатели примерно в 7 и 30 раз выше, чем у балки квадратного поперечного сечения такой же площади, cделанной из того же материала. Таким образом, рациональное расположение материала по сечению позволяет снизить его расход.
Как увидим дальше, этот вывод имеет обобщение на форму конструкции в
целом. Но в данный момент, отвлекаясь от физических свойств изучаемого объекта,
рассмотрим основные геометрические характеристики поперечных сечений стержня,
определяющие сопротивление различным видам его деформирования.
В расчетах конструкций на механическую надежность очень часто приходится оперировать такими характеристиками плоских фигур, как статический момент, осевой и полярный моменты инерции. Хотя вычисление вышеназванных геометрических характеристик относится к числу простейших задач интегрального исчисления, тем не менее, в силу их узкого прикладного значения они практически не рассматриваются во втузовском курсе высшей математики. По установившейся традиции геометрические характеристики плоских фигур изучаются в курсе сопротивления материалов.
Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).
Площадь плоских сечений
Площадь сечения является одной из геометрических характеристик, используемых, главным образом, в расчетах на растяжение и сжатие. При расчетах на кручение, изгиб, а также на устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции, моменты сопротивления и т.д.
Проектирование конструкций с оптимальными формами и размерами сечений является одним из путей снижения веса и стоимости машин и сооружений.
Площадь, ограниченная произвольной кривой, есть
Для вычисления геометрических характеристик сложных сечений, состоящих из простейших фигур, они разбиваются на конечное число n простейших частей. В этом случае
Площадь является простейшей геометрической характеристикой сечения, имеет размерность L2. Отметим два важных свойства: площадь всегда положительна и не зависит от выбора системы координат.
Для сечений, составленных из профилей стандартного проката, площадь каждого профиля и остальные необходимые для расчетов размеры принимаются по таблицам ГОСТов на прокатную сталь.
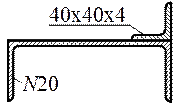
При расчетах на изгиб, кручение, сложное сопротивление и устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции сечений, которые зависят не только от формы и размеров сечений, но также от положения осей и точек (полюсов), относительно которых они вычисляются.
Статические моменты сечения
Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):
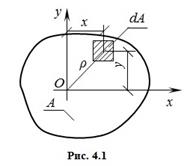
где yc – расстояние от центра тяжести всего плоского сечения до оси x; xc – расстояние от центра тяжести всего сечения до оси y.
Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:
В формулах (6) введены обозначения: А1, А2, …, Аn – площади простых элементов, составляющих плоское сложное сечение; x1, y1, x2, y2, x3, y3, … , xn, yn – координаты центров тяжести простых составляющих сложного плоского сечения относительно выбранных осей х и у.
Из выражений (4) можно определить координаты центра тяжести плоского сечения:
Для сложного поперечного сечения формулы (7) можно представить в следующем виде
Зависимости между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей х и х1, а также у и у1 имеют вид:
где параметры a, b показаны на рис. 4.2.
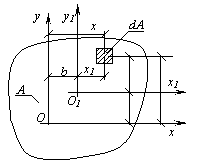
Рис.4.2
У к а з а н
и я.
1. Изменение положительного направления оси у вызывает изменение знака статического момента Sx. Аналогично, изменение положительного направления оси х вызывает изменение знака статического момента Sy.
2. Статический момент сечения равен нулю относительно любой оси, проходящей через центр тяжести этого сечения.
3. Если плоское сечение имеет ось симметрии, то эта ось всегда проходит через центр тяжести плоского сечения, а поэтому, согласно п.2, статический момент сечения относительно оси симметрии всегда равен нулю.
4. Если плоское сечение имеет две оси симметрии, то центр тяжести сечения лежит на пересечении этих осей симметрии.
Пример
1.
Определить статический момент полукруга радиусом R (рис. 4.3) относительно горизонтальной оси z, совпадающей с диаметром, и координату центра тяжести yc.
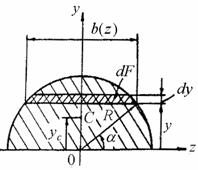
Рис.4.3
Решение.
По формуле (3)
имеем 
.
Выделим на рис. 4.3 на расстоянии y элементарную
площадку dF с помощью двух хорд, параллельных оси z, на
расстоянии dy друг от друга. Как следует из рис. 4.3
тогда
Подставляя найденные значения y и dF в выражение Sz, получим
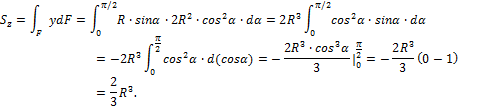
Координата центра тяжести сечения yc определяется по формуле (7):
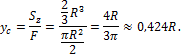
Пример
2.
Найти положения центра тяжести фигуры, имеющей форму тавра (рис.4.4).
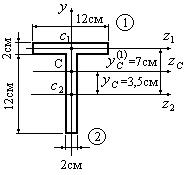
Рис.4.4
Решение.
1. Разбиваем изображенную на рис. 4.4 фигуру на простые и присваиваем им номера 1 и 2. Центры тяжести каждой из простых фигур обозначаем соответственно с1 и с2.
2. Проводим через центры тяжести каждой из фигур оси z1, z2 и ось y. Ось y является осью симметрии фигуры, проходит через центры тяжести обеих простых фигур и всей фигуры также и поэтому индексации не имеет.
3. Выбираем в качестве начала координат центр тяжести второй фигуры c2 и в качестве оси, относительно которой будем производить все вычисления, ось z2.
4. Вычислим статический момент площади фигуры относительно оси z2:
В формуле (а)
координата центра тяжести второй простой фигуры 
,
так как ось z2, относительно которой
определялся статический момент площади, проходит через центр тяжести второй
фигуры. В соответствии с основным своим свойством статический момент площади
относительно любой центральной оси равен нулю. В связи с этим для сокращения
арифметических вычислений при определении положения центра тяжести сложных
фигур рекомендуется выбирать в качестве начала координат центр тяжести одной из
простых фигур.
4. Находим координату центра тяжести всей фигуры, используя выражение (7):
Найденное значение координаты центра тяжести отложим вдоль оси y вверх от точки c2, так как это значение положительное. Полученную точку обозначим буквой C. Ось zC, проведенная через центр тяжести всей фигуры будет одной из центральных осей фигуры. Вторая центральная ось фигуры в данном примере не определяется, так как этой осью является ось симметрии y. Статические моменты Sy простых фигур и всей фигуры относительно этой оси равны нулю. В соответствии с выражением (7) координата центра тяжести всей фигуры zC =0.
Анализируя полученное решение, можно сделать вывод о том, что при определении центра тяжести для сложных фигур очень важно удачно выбрать начало координат и, соответственно, оси, относительно которых производятся все вычисления. Как уже отмечалось выше, начало координат следует помещать в центр тяжести одной из простых фигур.
Пример
3.
Определить
положение центра тяжести неравнобокого уголка 160
10010
(пренебрегая закруглениями его полок) относительно осей z и y, совпадающих с наружными
сторонами контура (рис. 4.5). Найденные значения координат сравнить с
табличными значениями по ГОСТ 8510-57.
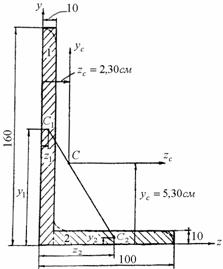
Рис.4.5
Решение.
Пренебрегая загружением полок уголка, разбиваем фигуру на два прямоугольника, как показано на рис. 4.5. Для первого (1) прямоугольника
Для второго (2) прямоугольника
Координаты центра тяжести сечения определяем по формулам (8):
По данным сортамента с учетом закруглений координаты центра тяжести равны zc=2,28см; yc=5,23см.
Для проверки правильности вычислений определим статические моменты относительно центральных осей, которые должны быть равны нулю:
Графическая проверка: точка С должна находиться на отрезке С1С2.
Моменты инерции плоских сечений простой формы
В дополнение к статическим моментам в системе координат x0y рассмотрим три интегральных выражения:
Первые два интегральных выражения называются осевыми моментами инерции относительно осей x и y, а третье - центробежным моментом инерции сечения относительно осей x, y.
Для сечений, состоящих из n-числа областей (рис. 4.6), формулы (10) будут иметь вид:
Рис. 4.6
Рассмотрим, как изменяются моменты инерции сечения при параллельном переносе координатных осей x и y (см. рис. 4.7). Преобразуя формулы (10), получим:
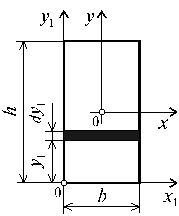
Рис. 4.7
Если
предположить, что оси x1 и
y1
(см. рис. 4.7) являются центральными, тогда 
и выражения (11) упрощаются и принимают вид:
Оси называются центральными, если они проходят через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю. Главными осями инерции фигуры называются оси относительно которых центробежный момент инерции равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
Определим осевые моменты инерции прямоугольника относительно осей x и y , проходящих через его центр тяжести (рис. 4.7). В качестве элементарной площадки dА возьмем полоску шириной b и высотой dy (рис. 4.7). Тогда будем иметь:
Аналогичным
образом можно установить, что 
Центробежный момент инерции сечения относительно осей, хотя бы одна из которых является осью симметрии, равен нулю.
Для систем, рассматриваемых в полярной системе координат (рис. 4.8, а), вводится также полярный момент инерции:
где 
- радиус-вектор
точки тела в заданной полярной системе координат.
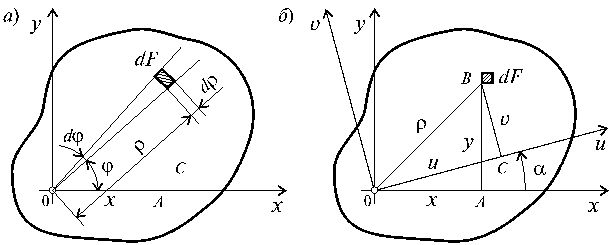
Рис. 4.8
Вычислим полярный момент инерции круга радиуса R. На рис. 4.8, a показана элементарная площадка, очерченная двумя радиусами и двумя концентрическими поверхностями, площадью
Интегрирование по площади заменим двойным интегрированием:
Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 4.8, б), что
следовательно,
Данное условие называется условием инвариантности. Формулируется условие инвариантности следующим образом: сумма осевых моментов инерции относительно двух любых взаимно перпендикулярных осей есть величина постоянная и равная полярному моменту инерции относительно точки пересечения этих осей.
Так как оси x и y
для круга равнозначны, то 
Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):
Размерность моментов инерции L4. Осевые и полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным, равным нулю.
Для фигур, имеющих более двух осей симметрии, осевые моменты инерции относительно всех центральных осей равны между собой. К таким фигурам относятся равносторонний треугольник, квадрат, круг и т.д.
Моменты инерции простых сечений
Вычислим моменты инерции простейших фигур.
Прямоугольник (рис. 4.9)
Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей (рис.4.9).
По определению
Рис. 4.9
Элемент площади равен dA=bdy,
следовательно 
По формуле 
,
откуда, учитывая что А = bh, yc = 0,5h, находим
Аналогично
получим 
и 
Треугольник
(рис. 4.10)
Момент инерции относительно оси х, cовпадающей с основанием,
Но
dA =
b(y)dy, b(y) = (b/h)(h-y).
Cледовательно,
Рис. 4.10
По формуле
параллельного переноса 
, откуда
Круг
(рис. 4.11)
Для любых
центральных осей 
, поэтому
Как известно,
полярный момент инерции круга равен 
Рис. 4.11
Следовательно,
Кольцо 
(рис.
4.12)
Момент инерции
относительно оси 
(рис.4.12) можно определить как разность
моментов инерции наружного и внутреннего круга:
Для тонкого
кольца существует приближенная формула 
,
где dср – средний диаметр, t - толщина
кольца.
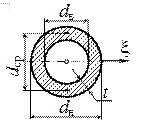
Рис. 4.12
Моменты инерции сечений сложной формы
Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:
что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.
Пример
4.
Определить осевые моменты инерции фигуры, приведенной
на рис. 4.13, относительно центральных осей zc и yc.
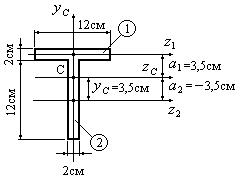
Рис.4.13
Решение:
В примере 2 для изображенной на рис.4.13 фигуры было определено положение центра тяжести С. Координата центра тяжести
откладывалась от оси z2 и
составила yc =3,5
см. Вычислим расстояния a1 и a2 между осями z1 и zc и осями z2 и zc. Эти расстояния составили соответственно a1 =3,5 см и a2 = -3,5
см. Так как исходные оси z1 и z2 являются центральными осями для простых фигур в виде
прямоугольников, для определения момента инерции фигуры относительно оси zc воспользуемся
формулой.
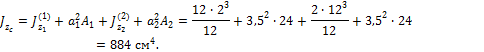
Момент инерции относительно оси yc получим
путем сложения моментов инерции простых фигур относительно этой же оси, так как
ось yc является общей центральной осью для простых
фигур и для всей фигуры.
Центробежный момент инерции относительно осей zc и yc равен нулю, так как ось инерции yc является
главной осью (осью симметрии фигуры).
Пример
5.
Определить
момент инерции сечения, показанного на рис. 4.14, относительно оси симметрии, a=10 см.
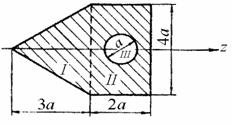
Рис.4.14
Решение.
Разбиваем заданное сечение на простейшие элементы: I - Равнобедренный треугольник, II - прямоугольник, III - круг.
Момент инерции сложной фигуры относительно оси z согласно формуле (13):
Определяем моменты инерции слагаемых простейших элементов:
Для равнобедренного треугольника:
для прямоугольника согласно формуле:
для круга согласно формуле:
Окончательно получим:
Iz= 4,0a4 + 10,67a4 - 0,0491a4 = 14,6a4 = 14,6×104 = 1,46×105 см4.
Пример
6.
Определить момент инерции симметричного сечения, показанного на рис. 4.15, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56).
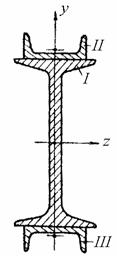
Рис.4.15
Решение.
Разбиваем исходное сечение на простейшие элементы, моменты инерций которых приводятся в справочниках: I - двутавр, II и III - швеллеры.
По сортаменту на стандартные прокатные профили имеем:
Для двутавра №10 (ГОСТ 8239-56): H=10 см, B=7 см, F=14,2 см2, Ix=244 см4, Iy=35,3 см4.
Для швеллера №5 (ГОСТ 8240-56): h=5 см, b=3,7 см, F=6,90 см2, Ix=26,1 см4, Iy=8,41 см4, x0=1,35 см.
Момент инерции сечения относительно оси y согласно (13)
т.к. оба швеллера расположены идентично относительно оси y.
Для двутавра 
Для швеллера 
Окончательно
имеем: 
Пример
7.
Чему равен размер b (в см) фигуры, изображенной на рис. 4.16, если момент инерции фигуры относительно оси z1 равен 1000 см4?
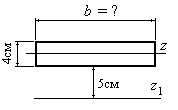
Рис.4.16
Решение.
Выразим момент инерции относительно оси z через неизвестный размер сечения b,
воспользовавшись формулами (12), учитывая, что расстояние между осями z и z1 равно 7 см:
Решая выражение (а) относительно размера сечения b, получим:
Пример
8.
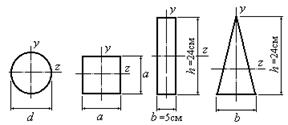
Какая из фигур, изображенных на рис.4.17, имеет больший момент инерции относительно оси z, если обе фигуры имеют одинаковую площадь A=400 см2?
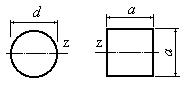
Рис.4.17
Решение.
1. Выразим площади фигур через их размеры и определим:
а) диаметр сечения для круглого сечения:
Откуда
б) размер стороны квадрата:
A = a2.
Откуда
2. Вычисляем момент инерции для круглого сечения:
3. Вычисляем момент инерции для сечения квадратной формы:
Сравнивая полученные результаты, приходим к выводу, что наибольшим
моментом инерции будет обладать сечение квадратной формы по сравнению с сечение
круглой формы при одинаковой у них площади.
Пример
9.
Определить полярный момент инерции (в см4) сечения прямоугольной формы относительно его
центра тяжести, если ширина сечения b=8 см, высота сечения h=24 см.
Решение.
1. Найдем моменты инерции сечения относительно
горизонтальной z и вертикальной y центральных осей инерции:
2. Определяем полярный момент инерции сечения как
сумму осевых моментов инерции:
Пример
10.
Определить момент инерции фигуры треугольной формы изображенной на рис.4.18, относительно центральной оси z, если момент инерции фигуры относительно оси z1 равен 2400 см4.
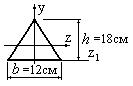
Рис.4.18
Решение.
Момент инерции сечения треугольной формы относительно главной оси
инерции z будет меньше по сравнению с моментом инерции
относительно оси z1 на величину a2A. Поэтому при a = h/3 = 6 см момент инерции сечения относительно оси z найдем
следующим образом:
Изменение моментов инерции сечения при повороте осей координат
Найдем
зависимость между моментами инерции относительно осей х, у и моментами инерции
относительно осей х1,
у1, повернутых на угол 
.
Пусть Jx >
Jy и положительный
угол отсчитывается от оси х против часовой стрелки. Пусть координаты точки М до поворота – x, y ,
после поворота – x1, y1
(рис. 4.19).
Рис.4.19
Из рисунка 4.19 следует:
Теперь определим моменты инерции относительно осей х1 и у1:
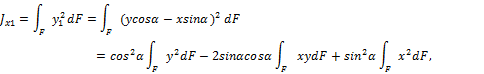
Аналогично:
Сложив почленно уравнения (14), (15), получим:
т.е. сумма моментов инерции относительно любых взаимно перпендикулярных осей остается постоянной и не изменяется при повороте системы координат (условие инвариантности).
Пример 11.
Найти моменты инерции
прямоугольника (рис.4.20) относительно осей 
и 
и центробежный момент его относительно тех же
осей.
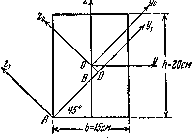
Рис.4.20
Решение.
Центральные оси у и z как оси симметрии будут главными осями; моменты инерции сечения относительно этих осей равны:
Центральные моменты относительно повернутых осей y0 и z0 равны:
Центробежный момент инерции относительно осей y0 и z0 равен:
Координаты центра тяжести прямоугольника относительно осей y1 и z1 равны:
Моменты инерции относительно осей y1 и z1 равны:
Центробежный момент инерции равен:
Пример 12.
Моменты инерции сечения прямоугольной формы
относительно главных осей равны соответственно Jz =400 см4, Jy =200
см4. При повороте на 450 моменты инерции относительно
новых осей оказались одинаковыми. Чему равна их величина?
Решение.
Для решения задачи воспользуемся выражением (14) с
учетом того, что центробежный момент инерции относительно главных осей равен
нулю:
Подставим в формулу (а) численные значения для
моментов инерции и угла поворота осей:
Главные оси инерции и главные моменты инерции
С изменением
угла поворота осей каждая из величин 
и 
меняется, а сумма их остается неизменной.
Следовательно, существует такое значение 
,
при котором моменты инерции достигают экстремальных значений, т.е. один из
моментов инерции достигает своего максимального значения, в то время другой
момент инерции принимает минимальное значение. Для нахождения значения 
возьмем первую производную от (или )
и приравняем ее нулю:
или
откуда
Покажем, что относительно полученных осей центробежный момент инерции равен нулю. Для этого приравняем правую часть уравнения (16) нулю:
откуда
т.е. получили
ту же формулу для .
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.
Обозначим
главные оси через 
и 
.
Тогда
Если сечение имеет ось симметрии, то эта ось всегда является одной из главных центральных осей инерции сечения.
В литературе главные оси иногда обозначаются через u и v.
Главные
моменты инерции 
и 
могут быть также определены по формулам:
При повороте осей координат удовлетворяется следующее равенство:
Моменты сопротивления относительно главных центральных осей u и v могут быть подсчитаны по формулам:
где 
- координаты точек сечения, наиболее удаленных
от главных центральных осей u и
v. Эти координаты можно вычислить, используя связь между
координатами в повернутых на угол осях по формулам:
Понятие о радиусе и эллипсе инерции сечения
Радиусом инерции плоской фигуры относительно какой-либо оси, называется длина перпендикуляра, отсчитываемая от этой оси и вычисляемая по формуле:
После
определения моментов инерции относительно главных осей можно построить эллипс
инерции – это эллипс, полуоси которого равны радиусам инерции
относительно главных осей. Радиус инерции 
откладывается вдоль главной оси Z, а 
– вдоль оси Y
(рис. 4.21). Построение эллипса инерции удобно использовать для анализа
правильности определения моментов инерции. Эллипс инерции должен быть вытянут в
том направлении, в котором вытянута фигура.
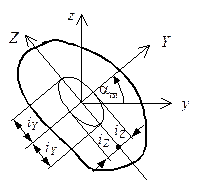
Рис.4.21
Пример
13.
Определить
радиусы инерции для сечения неравнобедренного уголка 16010010
(рис. 4.22). Построить эллипс инерции этого сечения.
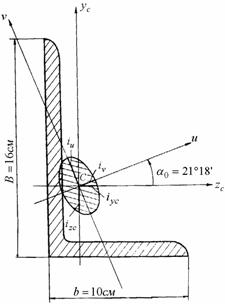
Рис.4.22
Решение.
Осевые радиусы инерций сечения определяются по формулам:
Aуголка №16/10 =25,3
см2
Построенный эллипс инерции показан на рис. 4.22.
Пример
14.
У которой из фигур (рис.4.23), имеющих одинаковую площадь, радиус инерции относительно оси z, будет наибольшим? Определить наибольший радиус инерции сечения относительно оси z.
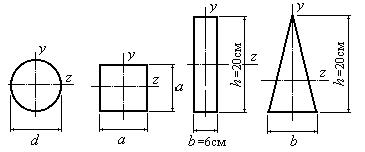
Рис.4.23
Решение.
1. Найдем площадь каждой из фигур и размеры сечений.
Площадь фигур одинакова. Площадь третьей фигуры A = A3 = b∙h = 6∙20 = 120
см2 = A1 = A2 = A4.
Диаметр первого сечения найдем из выражения:
Размер стороны квадрата:
Основание треугольника:
2. Находим моменты и радиусы инерции каждого из сечений относительно центральной
оси z.
Для сечения круглой формы:
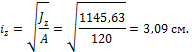
Для сечения квадратной формы:
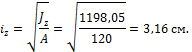
Для сечения прямоугольной формы:
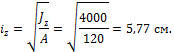
Для сечения треугольной формы:
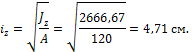
Наибольший радиус инерции оказался у сечения прямоугольной формы и
равен он iz = 5,77 см.
Пример
15.
Определить положение главных центральных осей и величину главных центральных моментов инерции для составного сечения (рис.4.24). Построить эллипс инерции.
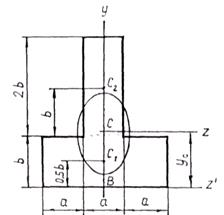
Рис.4.24
Решение.
Центр тяжести фигуры лежит на оси симметрии у, которая и является главной центральной осью.
Выбираем произвольную ось 
и
определяем ординату центра тяжести, предварительно разбив сечение на два
прямоугольника:
Через точку С перпендикулярно оси у проводим ось z, которая и будет другой главной центральной осью.
Для каждого из прямоугольников находим моменты инерции относительно их главных центральных осей:
а также расстояния их центров тяжести от оси z:
Используя зависимости между моментами инерции относительно параллельных
осей, находим величины главных центральных моментов инерции:
Определяем радиусы инерции:
и строим эллипс инерции (см. рис.4.24),
отложив величины iz и iy на
перпендикулярах к соответствующим осям.
Пример
17.
Определить положение главных центральных осей и вычислить величины главных центральных моментов инерции сечения, представленного на рис. 4.25, если b =0,1 м, h=0,2 м, d=0,05 м.
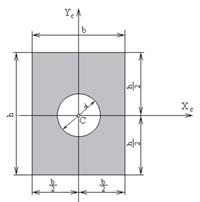
Рис.4.25
Решение.
Сечение, изображенное на рис.4.25, представляет собой прямоугольник с отверстием в виде круга с отрицательной площадью. Так как сечение имеет две оси симметрии, то центр тяжести сечения лежит в точке пересечения этих осей. Эти же оси в данном случае будут являться главными центральными осями.
Определяем главные моменты инерции сечения. Предварительно по формулам, приведенным в таблице, вычисляем моменты инерции элементарных фигур:
для прямоугольника
для круга
Момент инерции всего сечения относительно оси X равен
Пример
18.
Определить
положение главных центральных осей и вычислить главные центральные моменты
инерции сечения, представленного на рис. 4.26. Размеры на рисунке в
сантиметрах.
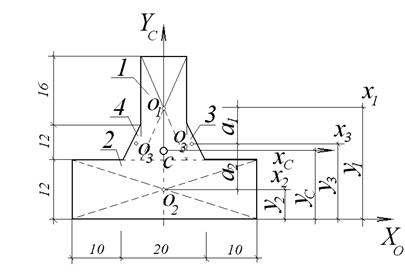
Рис.4.26
Решение.
Разбиваем сечение на простейшие фигуры: два прямоугольника – 1 и 2, два треугольника - 3 и 4. Положение центров тяжести простейших фигур известно из курса элементарной математики.
Выбираем положение вспомогательных осей, относительно которых будем отсчитывать координаты центра тяжести всего сечения. Так как сечение имеет одну ось симметрии (вертикальную), то эта ось является одной из главных осей. Остаётся определить положение центра тяжести на этой оси. Для этого проводим вспомогательную ось X0, от которой будем отсчитывать расстояния до центров тяжести элементарных фигур по вертикали: y1=26 см, y2=6 см, y3=16 см.
Площади этих простейших фигур равны:
A1 = 280 см2, A2= 480 см2, A3= 30 см2.
Вычисляем расстояние от оси X0 до центра тяжести всей фигуры по оси Y:
Отложив от оси X0 по оси Y отрезок равный 13,6 см, получим точку пересечения главных центральных осей Xc, Yc, т. е. положение центра тяжести всей фигуры с координатами xc, yc (рис.4.26).
Определяем главные центральные моменты инерции сечения.
Главный момент инерции сечения относительно оси Xc равен
Моменты инерции каждой составляющей фигуры всего сечения относительно оси Xc определяем по формуле перехода к параллельным осям:
где 
- моменты инерции простейших фигур
относительно собственных центральных осей X1, X2, X3; a1, a2, a3 - расстояния между указанными осями и главной
центральной осью Xc.
Согласно рис. 4.26, a1=12,4 см, a2 =7,6 см, a3=2,4 см.
Тогда моменты инерции (размерность - см4):
Главный момент инерции всего сечения относительно оси Xc равен
(В скобках приведено значение этой величины, выраженное в единицах размерности СИ),
Аналогично определяем величину главного момента инерции относительно оси Yc:
В данном примере ось Yc является главной как для всего сечения, так и для прямоугольников 1 и 2. Тогда моменты инерции каждой составляющей фигуры относительно оси Yc, (размерность - см4), равны:
Главный момент инерции всего сечения относительно оси Yc равен:
Пример
19.
Определить положение главных центральных осей и вычислить главные моменты инерции сечения, изображенного на рис. 4.27. Сечение состоит из прокатных профилей, все геометрические характеристики которых приведены в таблицах ГОСТа.
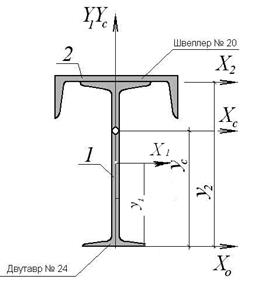
Рис.4.27
Решение.
Сечение состоит из двух прокатных профилей - двутавра № 24 и швеллера № 20. По табл. ГОСТ 8239-89 выписываем для двутавра № 24 необходимые геометрические характеристики: h = 24 см, площадь сечения А=34,8 см2, моменты инерции относительно собственных центральных осей Ix = 3460 cм4, Iy =198 см4. Аналогично выписываем из табл. ГОСТ 8240-89 геометрические характеристики для швеллера № 20: А =23,4 см2, Ix = 1520 cм4, Iy = 113 cм4, z0 = 2,07 см, d =0,52 см.
Определяем положение центра тяжести сечения. Выбираем вспомогательные оси Х0Y0. Так как сечение имеет одну ось симметрии, то совместим ось Y0 c этой осью, а ось X0 проведем через основание двутавра (рис.4.27). Тогда абсцисса центра тяжести xc равна нулю.
Определяем ординату центра тяжести yc по формуле:
где А1, А2
- площади сечений двутавра и швеллера; у1, у2 - ординаты
центров тяжести двутавра
и швеллера соответственно.
Используя найденные значения координат, проводим главные центральные оси Xc и Yc (главными они являются потому, что одна ось совпадает с осью симметрии). Точка пересечения осей (точка С) определяет центр тяжести.
Определяем главные моменты инерции сечения по формуле:
где:
В этих
выражениях 
-
момент инерции двутавра относительно собственной
центральной оси Х1
(в сортаменте Х); 
-
момент инерции швеллера относительно собственной центральной оси Х2 (в сортаменте Х); а1
-расстояние между осями Хс и Х1;
а2 - расстояние
между осями Хс
и Х2.
Тогда
Следовательно:
Вычисляем главный момент инерции составного сечения относительно оси Yc. Tак как ось Yc - ось симметрии и центры тяжести двутавра и швеллера лежат на этой оси, то b1=b2=0.
Тогда
Здесь 
=
Iy двутавра
по ГОСТ, 
= Iy швеллера по ГОСТ.
Тогда
Пример
20.
Найти расстояние с
между ветвями составного стержня, обеспечивающее
равенство главных моментов инерции сечения (рис.4.28).
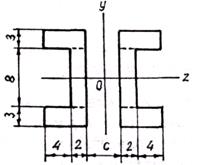
Рис.4.28
Решение.
Требуемое условие обеспечивается равенством моментов инерции
относительно осей симметрии z и у,
являющихся главными центральными осями сечения.
Разбиваем каждую часть сечения на три прямоугольника, как показано на
рис.4.19, и определяем моменты инерции:
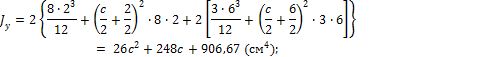
Приравнивая Jy и Jz, получаем уравнение
Или
откуда с = 4,19 см.
Здесь и отрицательный корень с
= –13,73 см имеет смысл. Читателю предлагается изобразить составное сечение для
этого случая.
Моменты сопротивления
Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
Полярный момент сопротивления
Осевой и полярный моменты инерции имеют размерность м3.
Стандартные прокатные профили
В балках из металла обычно применяются сложные поперечные
сечения, потому что в них материал может быть использован экономичнее, чем в
таких сечениях, как прямоугольник и круг.
Так, известно, что валы делают полыми, чтобы удалить ту
часть материала, которая слабо работает. Известно также, что при изгибе балок
материал около нейтральной оси принимает на себя малые нормальные напряжения и
также не может быть использован полностью. Поэтому целесообразнее переделать
прямоугольное сечение так, чтобы удалить материал у нейтральной оси и часть его
сэкономить, а часть перенести в верхнюю и нижнюю зоны балки, где он будет
работать более интенсивно. Так получается из прямоугольного сечения профиль двутавра,
обладающего той же прочностью и меньшим весом. Применение двутавра
целесообразно при материалах, одинаково сопротивляющихся растяжению и сжатию
(большинство металлов).
Сечения в виде тавра, применяются или в случаях,
вызываемых специальными конструктивными обстоятельствами, или для таких материалов,
как чугун, бетон, у которых сопротивления растяжению и сжатию резко разнятся
между собой; последнее обстоятельство требует, чтобы напряжения в крайних
волокнах были различными.
Как видно из изложенного, при решении вопроса о наиболее
экономичном проектировании сечения следует стремиться к тому, чтобы при одной и
той же площади F получить наибольший момент сопротивления и момент
инерции. Это ведет к размещению большей части материала подальше от нейтральной
оси.
Однако для некоторых сечений можно увеличить момент
сопротивления не добавлением, а, наоборот, путем срезки некоторой части
сечения, наиболее удаленной от нейтральной оси.
Так, например, для круглого сечения срезка заштрихованных
сегментов (рис.4.29) несколько увеличивает момент сопротивления, так как при
этом мы уменьшаем момент инерции сечения в меньшей степени, чем расстояние до
крайнего волокна 
.
Рис.4.29
Нашей промышленностью выпускаются стандартные прокатные профили (двутавр, швеллер, уголок равнобокий, уголок неравнобокий), которые могут быть использованы как готовые элементы конструкций (балки, стойки, элементы ферм и т.д.). Размеры прокатных профилей стандартизированы и сведены в таблицы сортаментов прокатной стали, которые приводятся в приложениях почти всех учебников и сборников задач по сопротивлению материалов. В этих таблицах приводятся все размеры сечений и основные геометрические характеристики прокатных профилей в соответствии с их номером.
Алгоритм расчета геометрических характеристик плоских сечений
При анализе геометрических характеристик плоских сечений любой сложности важнейшей задачей является определение положения главных центральных осей, величин главных центральных моментов инерции и моментов сопротивления сечений.
Можно рекомендовать следующий порядок определения положения главных центральных осей, величин главных центральных моментов инерции и моментов сопротивления сложного профиля, состоящего из простых частей, характеристики которых либо известны, либо легко определяются.
1. Заданное сечение вычерчивается в определенном масштабе и разбивается на элементы геометрические характеристики которых представлены в сортаменте, либо могут быть вычислены по элементарным формулам, элементы нумеруются, номера элементов указываются на чертеже.
2. Проводим прямоугольную систему осей z, y. Начальные оси могут задаваться произвольно. Однако, для упрощения вычислений удобно, если начальные оси проходят через центр тяжести одного или нескольких элементов сечения, на которые разбито заданное сечение. Все начальные размеры, необходимые для вычисления геометрических характеристик элементов и определения координат центров тяжестей элементов указываются на чертеже. Для прокатных профилей на чертеже сечения указываются необходимые для расчета размеры, взятые из таблиц проката.
3. Определяем координаты центров
тяжести элементов сечения относительно начальных осей zc, yc
и геометрические характеристики сечений относительно
собственных осей элементов Аi, 
Собственные оси элементов – оси, параллельные
начальным осям zc, yc. проходящие через центры тяжестей элементов
сечения.
Замечание. Необходимо проявлять внимательность при определении координат центров тяжестей элементов сечения и их геометрических характеристик, так как ошибки, допущенные на этом этапе не имеют алгоритма проверки и приводят к ошибочным результатам при дальнейших вычислениях.
4. Определяем координаты центра тяжести всего сечения по формулам:
Центральные оси х, у (оси проходящие через центр тяжести всего сечения), параллельные начальным осям показываются на чертеже.
Для самостоятельной
проверки правильности, определения координат центра тяжести сложного сечения
делается проверка, согласно которой вычисляются статические моменты всего
сечения относительно осей zc,
yc. Должны иметь
место равенства 
и 
в пределах точности производимых вычислений.
5. Проводим
систему центральных осей zc, yc, таким образом,
чтобы наиболее просто можно было вычислить моменты инерции частей фигуры
относительно этих осей. Для этого определяем моменты инерции частей фигуры
относительно собственных центральных осей, проведенных параллельно осям zc, yc, используя при этом формулы перехода к
параллельным осям (12). Суммируя, получаем значения 
6. Определяем координаты центров тяжести элементов сечения относительно центральных осей сечения:
Замечание. Геометрические характеристики сечений, координаты центров тяжести сечений относительно начальных и центральных осей целесообразно оформить в виде таблицы (см. пример расчета),
7. Проводим контроль правильности определения координат центров тяжести сечения и его элементов. Для этого вычисляется статический момент сечения относительно центральных осей, которые при правильном расчете должны равняться нулю:
Замечание.
Все расчеты проводятся с ограниченной точностью. Инженерные расчеты, обычно,
проводят с учетом 3 – 4 значащих цифр. Оставлять большее число значащих цифр
нецелесообразно, так как исходные данные (исходные размеры и значения
геометрических характеристик) не обеспечивают большую точность и поэтому
результаты с большим числом значащих цифр нельзя считать более достоверными.
Точность результата оценивают, обычно, относя невязку (разность между
приближенным и точным значением) к точному или приближенному значению. Однако,
если результатом вычислений должен быть ноль, такой подход невозможен. В этом
случае отдельно подсчитывают положительные 
и отрицательные 
слагаемые и абсолютное значение невязки и
относят невязку к сумме положительных (или отрицательных) слагаемых:
Погрешность инженерных расчетов обычно не должна превышать 3%.
8. Определяем геометрические характеристики сечения – осевые, полярный и центробежный моменты инерции сечения относительно центральных осей
Заметим, что площадь, осевые и полярный моменты инерции являются строго положительными характеристиками сечений. Однако, для сечений с отверстиями бывает удобным считать отверстия элементами сечений с отрицательными характеристиками.
9. Определяем
положение главных центральных осей. Положительный угол откладывается против хода часовой стрелки,
отрицательный - по ходу часовой стрелки.
10. Определяем
значения главных центральных моментов инерции 
и 
,
причем ось, относительно которой имеет место максимальный, главный центральный
момент инерции, обозначаем буквой u (Imax=Iu), а ей перпендикулярную ось,
относительно которой имеет место минимальный, главный центральный момент
инерции, обозначаем буквой v (Imin=Iv).
Для самостоятельного контроля правильности решения задачи на данном этапе делаются следующие проверки:
а)
Определяется центробежный момент инерции относительно главных центральных осей 
,
который согласно определению должен быть равен нулю, Iuv=0.
б) Также могут быть определены главные центральные моменты инерции сложного сечения Iu, Iv.
в) Должно удовлетворяться равенство:
11. Для определения моментов сопротивления сложного сечения необходимо определить точки, наиболее удаленные от главных центральных осей, координаты которых относительно главных центральных осей umax и vmax могут быть определены по формулам перехода к повернутым осям.
Для проверки, координаты точек, наиболее удаленных от главных центральных осей, могут быть определены и графически непосредственно с чертежа, выполненного в масштабе.
12. Для
определения радиусов инерции производятся вычисления по формулам (18). При
построении эллипса инерции от центра тяжести сечения по осям u и v откладываем
в масштабе чертежа величины iv и iu каждый соответственно перпендикулярно своей оси. На этих
отрезках, как на полуосях, строится эллипс инерции. Для проверки (или более
точного построения эллипса инерции) могут быть отложены величины 
и 
.
Вопросы для самопроверки
- Что называют поперечным сечением стержня?
- Для чего необходимы геометрические характеристики плоских сечений?
- Что такое статический момент плоской фигуры? Какова его размерность?
- Какими свойствами обладает статический момент?
- Относительно каких осей статический момент равен нулю?
- Какую размерность имеет статический момент сечения?
- Как определяется положение центра тяжести сечения?
- Каким соотношением связаны площадь, статические моменты и координаты центра тяжести фигуры?
- Вывести формулы для определения осевых моментов инерции простых фигур: прямоугольник, круг.
- Выведите зависимости между осевыми и центробежным моментами инерции сечения для параллельных осей.
- Как определяются координаты центра тяжести сложного сечения?
- Что понимается под осевым, полярным и центробежным моментами инерций? Какими свойствами они обладают? Их размерность?
- Что такое полярный момент инерции?
- Почему осевые и полярные моменты инерции не могут быть отрицательными?
- Относительно какой из параллельных осей осевой момент инерции наименьший?
- Когда используют полярный момент сопротивления?
- Размерность моментов инерции сечения?
- Для определения каких напряжений используют осевой момент сопротивления?
- Как записываются формулы перехода для моментов инерции при параллельном переносе осей?
- Какие свойства имеют главные центральные моменты инерции сечений?
- Как определяют главные моменты инерции сложных сечений, имеющих оси симметрии?
- У каких фигур положение главных центральных осей можно указать без вычислений?
- Какие оси являются главными центральными у симметричной фигуры?
- Какими экстремальными свойствами обладают главные оси?
- Как определяется угол поворота осей до положения главных?
- Чему равен осевой момент инерции относительно центральной оси?
- Чему равен осевой момент инерции для круга и кольца?
- Какие оси называются главными центральными осями инерции?
- Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?
- Какой зависимостью связаны осевые моменты инерции относительно центральной оси и параллельной ей нецентральной?
- Какой зависимостью связаны осевые моменты инерции прямоугольника относительно осей симметрии?
- Какой зависимостью связаны осевые моменты инерции треугольника относительно центральной оси, параллельной стороне?
- Какой зависимостью связаны осевые моменты инерции круга и кольца относительно центральной оси?
- Какая ось из множества параллельных осей сообщает осевому моменту инерции минимум?
- Как изменяется осевой момент инерции при повороте оси?
- Изменяется ли сумма осевых моментов инерции относительно взаимно перпендикулярных осей при повороте координатной системы?
- Какой из двух моментов инерции треугольника больше: относительно оси, проходящей через основание, или относительно оси, проходящей через вершины параллельно основанию?
- Какой из двух моментов инерции квадратного сечения больше: относительно центральной оси, проходящей параллельно сторонам, или относительно оси, проходящей через диагональ?
- От чего зависит знак центробежного момента инерции сечения?
- Какими выражениями определяются величины главных моментов инерции и положение главных осей? Получите эти выражения?
- Для каких сечений положение главных осей можно указать без вычислений?
- Получите соотношение между осевыми и полярными моментами инерции сечения?
- Получите выражения главных центральных моментов инерции для прямоугольного и кругового сечений?
- Что такое момент сопротивления сечения? Чему он равен для прямоугольного и круглого сечения?
- Что такое радиус инерции?
- Как строится эллипс инерции сечения? Для чего он строится?
- Что такое главные центральные оси инерции и почему необходимо вычислять значения главных моментов инерции относительно главных центральных осей?
- Как определяют главные моменты инерции и положение главных осей?
- Чему равен центробежный момент инерции относительно главных осей инерции?
- Как изменяется центробежный момент инерции при повороте осей?
- Какой зависимостью связаны центробежные моменты инерции относительно центральных осей и параллельных им нецентральных?
- Как без вычислений определить знак центробежного момента инерции равнобокого уголка относительно центральных осей, параллельных полкам?
- По каким формулам определяются полярные моменты инерции круга и кольца относительно их центров?
- Какие центральные оси являются главными у сечений, имеющих более двух осей симметрии?
- Почему производят разбивку сложного сечения на составляющие простые части при определении статических моментов и моментов инерции сечения?
- Какая геометрическая характеристика используется при определении прогиба?
- Какая геометрическая характеристика используется при определении угла закручивания?
- Какая геометрическая характеристика используется для определения максимальных касательных напряжений при кручении и максимальных нормальных напряжений при изгибе?
- Назовите основные геометрические характеристики поперечных сечений.
- Какие оси называются центральными осями ?
- Напишите зависимости между моментами инерции относительно параллельных осей.
- Как изменяются моменты инерции при повороте координатных осей?
- Какие оси и какие моменты инерции называются главными ?
- Напишите значения моментов инерции для простых сечений: прямоугольника, треугольника, круга, полукруга.
- В какой последовательности определяется положение главных центральных осей для составных сечений?
- Вычислите полярный момент инерции круга диаметром 80 мм?
- Вычислите полярный момент инерции поперечного сечения трубы? Наружный диаметр трубы dн=100 мм, внутренний dв=90 мм.
- Определите, на сколько процентов уменьшится полярный момент инерции кольца по сравнению с кругом, если наружный диаметр кольца dн равен диаметру круга d? Отношение внутреннего диаметра кольца к наружному
- Диаметр сплошного вала
увеличили в 2 раза. Во сколько раз увеличатся осевые моменты инерции? (
)
- Осевые моменты сечения равны соответственно Jx = 2,5 мм4 и Jy = 6,5 мм4. Определите полярный момент сечения?
- Осевой момент инерции кольца относительно оси Ох Jx=4 см4. Определите величину Jp?
- Вставьте (устно) пропущенное слово: Статическим моментом площади сложного сечения называется сумма произведений площадей на расстояние от … до их центров тяжести.
- Вставьте (устно) пропущенные слова: Координата центра тяжести сечения yc определяется как отношение суммы … к сумме …..
- Вставьте (устно) пропущенные слова: Осевым моментом инерции площади поперечного сечения называется взятый по всей площади сечения F интеграл от произведения элементарных площадок на … их расстояния от … до этих площадок.
- Зависит ли статический момент сечения от расстояния фигуры до оси, относительно которой он вычисляется?
- Во сколько раз изменится осевой момент инерции Izc сечения бруса, если он от круглого сечения был обработан до квадратного?
- Определите imin прямоугольного сечения со сторонами a и 4a.
- Определите ioc для круглого сечения диаметром d=16 см.
- Вычислить момент инерции сплошного круглого сечения диаметром d=4 см относительно центральной оси.
- Определить, на сколько (в %) уменьшится площадь и полярный момент инерции кольцевого сечения по сравнению со сплошным круглым, если наружный диаметр кольца Д равен диаметру круга Д. Отношение внутреннего диаметра кольца d к наружному Д равно 0,5.
- Для плоского сечения F оси x, y являются
1. центральными осями, если
2. главными осями, если
- Заполните таблицу для геометрических характеристик плоского сечения F, выбирая обозначения и расчётные формулы из следующих двух списков:
|
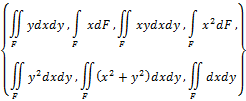
Геометрическая характеристика |
Обозначение |
Расчётная формула |
|
Статический момент относительно оси x |
|
|
|
Площадь сечения |
|
|
|
Центробежный момент инерции |
|
|
|
Полярный момент инерции |
|
|
|
Осевой момент инерции относительно оси x |
|
|
|
Статический момент относительно оси y |
|
|
- Для заданных
сечений определить: статические моменты площади относительно оси х0,
центробежный момент инерции 
,
осевые моменты инерции 
,
принять а=5 см, h =10 cм, b = 6 см , D = 8 см, 
а) б) в) г)
а)
1) 
2) 
3) 
б)
1) 
2) 
3) 
в)
1) 
2) 
3) 
г)
1) 
2) 
3) 
- На каком расстоянии от основания фигуры лежит центр тяжести фигуры, изображенной на рисунке?
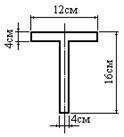
- Чему равен момент инерции фигуры, изображенной на рисунке, относительно оси z?
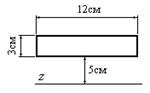
- Чему равен размер b (в см) фигуры, изображенной на рисунке, если момент инерции фигуры относительно оси z1 равен 882 см4?
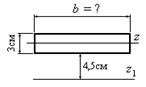
- Центр тяжести изображенной на рисунке фигуры лежит в точке С. Чему равен момент инерции фигуры (в см4) относительно оси z?
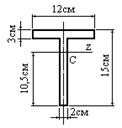
- Определить полярный момент инерции (в см4) сечения прямоугольной формы относительно его центра тяжести, если b=6 см, h=12 см.
- Определить момент инерции фигуры треугольной формы относительно центральной оси z, если момент инерции фигуры относительно оси z1 равен 1728 см4.
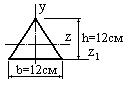
- Определить осевой момент инерции сечения квадратной формы, если полярный момент инерции сечения относительно центра тяжести Iρ=2440 см4.
- Моменты инерции сечения прямоугольной формы относительно главных осей равны соответственно Iz=200 см4, Iy=100 см4. При повороте на 450 моменты инерции относительно новых осей оказались одинаковыми. Чему равна их величина?
- Определить радиус инерции для плоской фигуры, имеющей форму круга диаметром d=12 см.
- У которой из фигур, имеющих одинаковую площадь, радиус инерции относительно оси z, будет наибольшим? Определить наибольший радиус инерции сечения относительно оси z. Результат округлить до целого значения.
Онлайн-калькулятор "Расчет геометрических характеристик круга"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
