Главная
Лекция 15 (продолжение). Примеры решения на динамические нагрузки
Расчеты при циклических нагрузках
Упругие
колебания систем с одной степенью свободы
Пример 1.
На конце стальной консоли длиной 1 м (см. рис.), выполненной из двутавра № 8, находится двигатель весом Р = 1230 Н.
Требуется определить частоты и периоды свободных колебаний системы – поперечных (изгибных) и продольных, пренебрегая собственным весом балки.
![]()
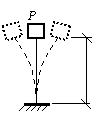
Решение.
Изгибные колебания. Воспользуемся
формулой ![]() Здесь xst – прогиб конца
консоли, нагруженной сосредоточенной силой Р.
Воспользуемся известной в сопротивлении материалов формулой для этого
прогиба
Здесь xst – прогиб конца
консоли, нагруженной сосредоточенной силой Р.
Воспользуемся известной в сопротивлении материалов формулой для этого
прогиба
![]()
В таком случае круговая частота изгибных колебаний
![]()
Период свободных изгибных колебаний равен
![]()
Продольные колебания. В этом случае xst – продольное перемещение свободного торца
консоли, нагруженной осевой сосредоточенной сжимающей силой Р = 1230 Н. Это перемещение равно продольной абсолютной деформации
стержня, которая рассчитывается по формуле: ![]()
В таком случае круговая частота продольных свободных колебаний балки равна
![]()
Рассчитываем период продольных свободных колебаний балки
![]()
Пример 2.
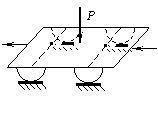
Определить круговую частоту вертикальных симметричных колебаний кузова тележки общим весом Р= 80 кН, укрепленного на двух осях с помощью четырех рессор, каждая из которых имеет жесткость с1 = 2·105 Н/м. Расчетная схема конструкции представлена на рисунке.
Решение.
Воспользуемся
формулой ![]() и учтем, что в нашем
случае параллельное соединение упругих связей, когда жесткости просто
складываются, т.е. с = 4с1; кроме того, Р = mg. Таким образом,
получаем следующее выражение для круговой частоты свободных колебаний системы:
и учтем, что в нашем
случае параллельное соединение упругих связей, когда жесткости просто
складываются, т.е. с = 4с1; кроме того, Р = mg. Таким образом,
получаем следующее выражение для круговой частоты свободных колебаний системы:
![]()
Пример 3.
Определить
круговую частоту и период свободных продольных колебаний стального стержня
квадратного поперечного сечения со стороной а
= 0,02 м и длиной 2 м, несущего на конце массу mг =
150 кг. Модуль продольной упругости стали Е
= 2·105 МПа, плотность ![]() = 7,75 г/см3 .
= 7,75 г/см3 .
Решение.
Как ранее отмечалось, в данном случае масса системы складывается из массы mг груза и приведенной к точке распределенной собственной массы стержня mo , т.е.
m = mг + αmо,
где ![]() , α = 0,33.
, α = 0,33.
Жесткость с найдем как силу, вызывающую единичную абсолютную деформацию стержня:
![]() , поэтому
, поэтому ![]()
Далее используем формулу для расчета круговой частоты свободных колебаний

Рассчитываем период свободных колебаний
![]()
Вынужденные
колебания систем с одной степенью свободы
Пример 4.
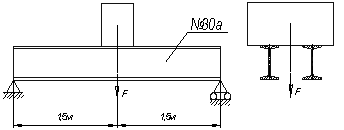
На двух двутавровых балках № 12 посередине установлен двигатель весом Q = 7 кН (см. рис.). Неуравновешенные массы двигателя условно заменены вращающимся со скоростью n = 550 об/мин грузом Q2 = 120 Н, радиус вращения которого R = 0,21 м.
Проверить прочность балок, приняв их длину l = 1,6 м, модуль упругости материала балок Е = 2·105 МПа, расчетное сопротивление стали изгибу, растяжению по пределу текучести Ry = 220 МПа.
Коэффициент
условий работы балок ![]() .
.

Решение.
1. Выписываем
из сортамента геометрические характеристики поперечного сечения двутавровой
балки и устанавливаем вес Q1
одной балки: ![]() момент инерции Iz
= 350 см4, момент сопротивления Wz = 58,4 см3, масса 1 м двутавра № 12 q = 11,5 кг/м. Масса одной балки m1 = ql =
11,5·1,6 = 18,4 кг; вес Q1 одной балки
момент инерции Iz
= 350 см4, момент сопротивления Wz = 58,4 см3, масса 1 м двутавра № 12 q = 11,5 кг/м. Масса одной балки m1 = ql =
11,5·1,6 = 18,4 кг; вес Q1 одной балки
![]() H.
H.
В дальнейшем расчет проводится
для одной балки (из двух).
2.
Рассчитаем собственную круговую частоту колебаний ![]() системы, для чего
воспользуемся формулой
системы, для чего
воспользуемся формулой
![]()
где yst – прогиб посередине балки, вызванный весом Q /2 и весом балки Q1.
Следует учесть, что при расчете собственной частоты балки, как системы с одной степенью свободы, в расчет вводится приведенная масса
![]() .
.
Для балки на
двух опорах коэффициент привидения ![]() .
.
При расчете yst можно использовать известную в теории изгиба балок формулу
![]() (1)
(1)
которая в данной задаче принимает вид
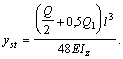
Таким образом, частота собственных колебаний системы равна
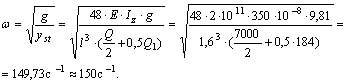
3. Рассчитаем
максимальное напряжение ![]() в среднем сечении
балки, нагруженной статически приложенными силами Q /2 и Q1 = qlg,
в среднем сечении
балки, нагруженной статически приложенными силами Q /2 и Q1 = qlg,

4. Рассчитаем
коэффициент нарастания колебаний ![]() по формуле
по формуле 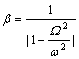 , установив предварительно величину частоты
, установив предварительно величину частоты ![]() возмущающей силы
возмущающей силы
![]()
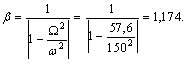
5. Рассчитаем
динамический коэффициент kd, используя формулу ![]()
Для этого по известным из теории изгиба балок формулам определим прогибы: yst(Q2) – прогиб посередине балки, от статической сосредоточенной силы Р0, равной силе инерции груза Q2 /2
![]() ,
,
т.е., применяя формулу (1), находим
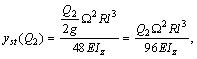
yst(Q,Q1)
= yst(Q) + yst(Q1) – прогиб посередине балки, нагруженной
статической сосредоточенной силой Q /2 и равномерно распределенной нагрузкой q = Q1 / l
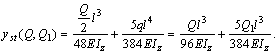
Определим отношение прогибов
![]()
Рассчитываем динамический коэффициент
![]()
6. Проверяем выполнение условия прочности
![]()
![]() МПа < 220 МПа.
МПа < 220 МПа.
Ответ: число оборотов двигателя n = 550 об/мин является безопасным для прочности балок.
Пример 5.
Используя условия предыдущего примера (кроме числа оборотов n), установить безопасный по прочности балок режим работы двигателя, т.е. определить допускаемое число оборотов.
Решение.
Используем из
решения предыдущей задачи отношение прогибов ![]() не подставляя в него
численного значения частоты
не подставляя в него
численного значения частоты ![]() возмущающей силы
возмущающей силы
![]()
Запишем
условие прочности ![]()
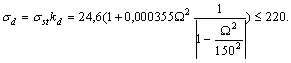
Далее решаем
неравенство![]()
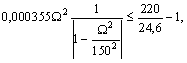 откуда
откуда ![]()
или ![]()
Возможны 2 случая:
1-й случай: ![]()
2-й случай: ![]()
Ответ:
допускаемое по прочности балок число оборотов двигателя ![]() об/мин.
об/мин.
Пример 6.
Двигатель
весом 12 кН укреплен посредине пролета ℓ =
Решение.
Частота собственных колебаний груза определяется по формуле
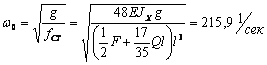
Частота изменения возмущающей силы равна
![]()
Коэффициент нарастания колебаний
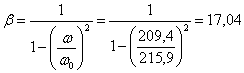
Динамический коэффициент
![]()
Наибольшее нормальное напряжение в балках равно
![]()
Пример 7.
На консоли из двух швеллеров № 27 (см. рис., а, б) установлен двигатель с массой т=2300 кг и частотой вращения п = 720 мин-1. Определить круговую частоту собственных колебаний и проверить систему на резонанс.
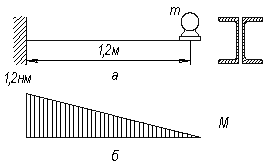
Решение.
Используем
выражение частоты ![]() где
где ![]() - перемещение от единичной силы, приложенной в месте
установки двигателя,
- перемещение от единичной силы, приложенной в месте
установки двигателя, ![]() здесь
здесь ![]() МНм2.
МНм2.
Перемещение от
единичной силы ![]() ;
;
Круговая
частота собственных колебаний ![]() .
.
Частота вынужденных
колебаний ![]() ;
;
Относительная
разница частот ![]()
![]() что более 30%, т.е.
опасности резонанса нет.
что более 30%, т.е.
опасности резонанса нет.
Пример 8.
Электродвигатель
массой т =![]() =
100 МПа, допускаемый прогиб
=
100 МПа, допускаемый прогиб ![]()
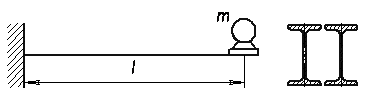
Решение.
Статический прогиб на конце балки
![]()
![]()
здесь ![]() вес двигателя.
вес двигателя.
Круговая частота собственных колебаний
![]()
Частота
возмущающей силы ![]() , поэтому
, поэтому ![]() , что более 30%, поэтому резонанс не опасен.
, что более 30%, поэтому резонанс не опасен.
Статическое
напряжение 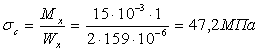 ,
,
Коэффициент
динамичности 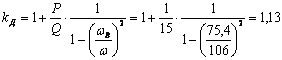 ,
,
Динамическое
напряжение ![]() , т.е. прочность обеспечена.
, т.е. прочность обеспечена.
Динамический прогиб ![]() ,
,
поэтому жесткость тоже обеспечена.
Пример 9.
На стальной
балке установлен электродвигатель весом G = 20 кН, совершающий n = 500 об/мин. Центробежная сила, возникающая вследствие
неуравновешенности частей двигателя составляет F =0,2G. Подобрать двутавровое поперечное сечение балки из условия
отстройки от резонанса ![]() , определить максимальный прогиб и максимальные напряжения.
Собственный вес балки не учитывается l =
, определить максимальный прогиб и максимальные напряжения.
Собственный вес балки не учитывается l =
Решение.
Находим частоту вынужденных колебаний.
![]() с-1
с-1
Определяем частоту свободных колебаний из условия отстройки от резонанса.
![]() с-1
с-1

Определяем прогиб от единичной силы по способу Верещагина
Эпюра момента от действия единичной силы показана на рисунке. Для нахождения прогиба перемножаем эту эпюру саму на себя.
![]()
Подбираем поперечное сечение
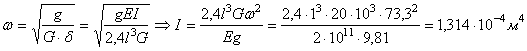
По ГОСТ 8239 – 89 подбираем двутавр № 36: IX = 13380 см4, WX = =743см3.
Определяем частоту свободных колебаний системы
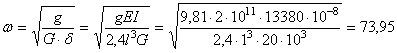 с-1
с-1
Определяем динамический коэффициент

Определяем наибольшие напряжения в балке
Определяем напряжения от веса двигателя
![]()
Определяем напряжения от статического действия центробежной силы
Так как ![]() , то статические напряжения от F найдем по
формуле:
, то статические напряжения от F найдем по
формуле:
![]()
Определяем динамические напряжения от центробежной силы
![]()
Определяем полные напряжения
![]()
Определяем наибольший прогиб балки
Определяем статический прогиб от действия центробежной силы
![]()
Определяем динамический прогиб от действия центробежной силы
![]() м
м
Определяем статический прогиб балки от веса двигателя
![]() м
м
Определяем полный прогиб
![]() м
м
Пример 10.
На двух
балках двутаврового сечения №16 (рис. 1) установлен двигатель весом Q =2,1 т, делающий n = 400 об/мин. Центробежная сила инерции, возникающая вследствие
неуравновешенности вращающихся частей двигателя, равна H = 1,1 т. Собственный вес
балок и силы сопротивления можно не учитывать. Требуется найти: 1) частоту
собственных колебаний ![]() ; 2) частоту изменения возмущающей силы
; 2) частоту изменения возмущающей силы ![]() ; 3) коэффициент нарастания колебаний
; 3) коэффициент нарастания колебаний ![]() (если коэффициент
(если коэффициент ![]() , определяемый по этой формуле, окажется отрицательным, то в
дальнейшем расчете следует учитывать его абсолютную величину); 4) динамический
коэффициент
, определяемый по этой формуле, окажется отрицательным, то в
дальнейшем расчете следует учитывать его абсолютную величину); 4) динамический
коэффициент ![]() ; 5) наибольшее нормальное
напряжение в балках
; 5) наибольшее нормальное
напряжение в балках ![]() .
.
1. Определим
частоту собственных колебаний ![]() . Для упругих систем с одной степенью свободы без учета
собственной массы
. Для упругих систем с одной степенью свободы без учета
собственной массы ![]() определяется по
формуле:
определяется по
формуле:
![]() ,
,
где уСТ – перемещение точки приложения веса двигателя
при статическом действии этого веса;
g – ускорение
силы тяжести, 981 см/с2.
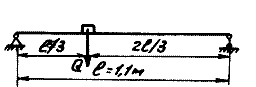
Рис.1
Определим уСТ,
воспользовавшись методом сил.
Строим эпюру ![]() (грузовую): Определим
реакции опор (рис. 2) от действия силы Q:
(грузовую): Определим
реакции опор (рис. 2) от действия силы Q:
![]() ;
;
![]() ,
, ![]() ,
,
![]() ;
; ![]() ,
,
![]() .
.
Применив метод
характерных сечений 1, 2, 3, 4, получим:
М1 =
0, ![]() , М4 = 0.
, М4 = 0.
Строим грузовую эпюру.
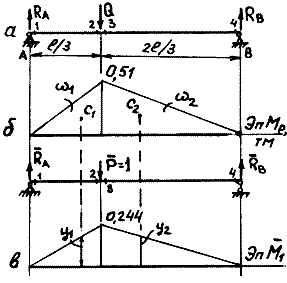
Рис.2
Определим
реакции опор от действия единичной силы ![]() = 1:
= 1:
![]() ;
; ![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Строим эпюру ![]() (единичную):
(единичную):
М1 =
0; ![]() ; М4 =
0, (рис. 2, в)
; М4 =
0, (рис. 2, в)
и вычислим статический прогиб, используя способ
Верещагина:
![]() ,
,
где ![]() – площади составляющих
грузовой эпюры;
– площади составляющих
грузовой эпюры;
уi – ординаты единичной эпюры под центрами
тяжести составляющих площадей грузовой эпюры;
Е = 2×106 кГс/см2 – модуль Юнга;
![]() – осевой момент
инерции сечения.
– осевой момент
инерции сечения.
Для двух
балок двутаврового сечения №16 ![]() см4.
см4.
![]()
![]()
тогда
![]()
2. Определим
частоту изменения возмущающей силы:
![]()
3. Определим
коэффициент нарастания колебаний:
![]()
Определим
динамический коэффициент
![]()
Определим наибольшее нормальное
динамическое напряжение в балке
![]() ,
,
где Mmax– максимальный изгибающий момент при действии силы Q статически, т.е. Mmax=MF,max= 0,51 Нм (рис. 2, б);
Wх –
момент сопротивления сечения. Для двух балок двутаврового сечения №16 ![]() см3.
Окончательно получим:
см3.
Окончательно получим:
![]()
Пример 10.
На двух
балках двутаврового сечения (рис. а) установлен двигатель весом Р, делавший n оборотов в минуту. Центробежная сила
инерции, возникающая вследствие неуравновешенности вращающихся частей двигателя,
равна Н.
Собственный вес балок и силы сопротивления можно не учитывать.
Требуется
найти: 1) частоту собственных колебаний ![]() ; 2) частоту изменения возмущающей силы
; 2) частоту изменения возмущающей силы ![]() ; 3) коэффициент нарастания колебаний
; 3) коэффициент нарастания колебаний ![]() ; 4) динамический коэффициент КД; 5) наибольшее нормальное
напряжение в балках, если дано: двутавр №20, l =
; 4) динамический коэффициент КД; 5) наибольшее нормальное
напряжение в балках, если дано: двутавр №20, l =
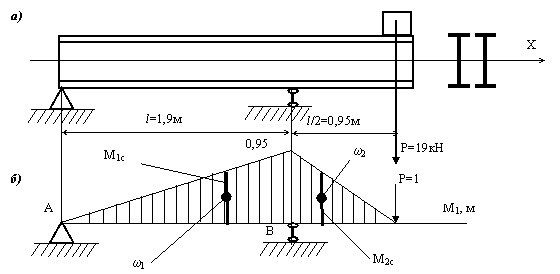
Решение.
1. По способу
Верещагина определяем прогиб сечения балки в месте расположения двигателя от
вертикальной силы, равной единице (рисунок 1, б):

если учесть,
что
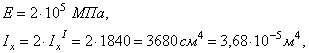
где IXI = 1840 см4 – по ГОСТ 8239-89 осевой момент инерции для двутавра №20.
Тогда
![]()
По формуле
находим частоту собственных колебаний
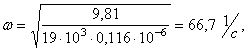
где g = 9,81 м/с2.
2.
Вертикальная составляющая центробежной силы Н представляет собой периодическую
силу,
вызывающую поперечные колебания в вертикальной плоскости.
![]()
Частота
изменения возмущающей силы Н(t) будет равна
![]()
где n – число оборотов вала двигателя в
минуту.
3.Определяем
коэффициент нарастания колебаний по формуле:
![]()
Так как
коэффициент ![]() оказался
отрицательным, то в дальнейшем расчёте учитываем абсолютную величину.
оказался
отрицательным, то в дальнейшем расчёте учитываем абсолютную величину.
4. Определяем
динамический коэффициент
![]()
5. Определяем
полное наибольшее нормальное напряжение в балке. Сечение В (рис. а):
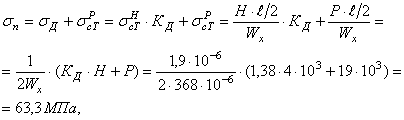
где WX = 2WXI =
2·184 = 368 см3 = 368·10-
Пример 12.
На балку с
сосредоточенной массой ![]() действует возмущающая нагрузка F(t) (рис. 1). Требуется построить эпюру изгибающих
моментов от динамического действия нагрузки. Примем следующие исходные данные:
действует возмущающая нагрузка F(t) (рис. 1). Требуется построить эпюру изгибающих
моментов от динамического действия нагрузки. Примем следующие исходные данные: ![]() кг, жесткость балки
кг, жесткость балки ![]() кНм2, ее длина
кНм2, ее длина ![]() м, отношение частоты вынужденных колебаний к частоте
собственных колебаний
м, отношение частоты вынужденных колебаний к частоте
собственных колебаний ![]() , амплитудное значение возмущающей нагрузки
, амплитудное значение возмущающей нагрузки ![]() кН.
кН.
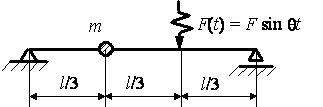
Рис.1
Теоретические
сведения.
Свободные (собственные) колебания – это колебания системы после сообщенного ей начального импульса. Их частота зависит от упругих свойств системы и при наличии сил сопротивления собственные колебания постепенно затухают. Вынужденные колебания происходят под действием возмущающих внешних сил. При изучении колебаний упругие системы различают по числу степеней свободы, то есть по числу независимых координат, определяющих положение системы. На рис. 2 изображена балка, с колеблющейся массой m. Если массой самой балки можно пренебречь по сравнению с колеблющейся массой, то эта система имеет одну степень свободы, так как положение массы полностью определяется ее вертикальной координатой.

Рис.2
Для систем с
одной степенью свободы круговая частота свободных
колебаний, то есть число колебаний за ![]() секунд определяется по
формуле:
секунд определяется по
формуле:
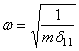 ,
(1)
,
(1)
где ![]() – перемещение сечения
с сосредоточенной массой
– перемещение сечения
с сосредоточенной массой ![]() по направлению ее
возможного движения, вызванное единичной силой, приложенной в том же сечении и
по тому же направлению. Для определения этого перемещения обычно используется
метод Максвелла – Мора.
по направлению ее
возможного движения, вызванное единичной силой, приложенной в том же сечении и
по тому же направлению. Для определения этого перемещения обычно используется
метод Максвелла – Мора.
Если на систему с одной степенью свободы действует возмущающая
сила, изменяющаяся по гармоническому закону ![]() и создающая
вынужденные колебания системы с частотой
и создающая
вынужденные колебания системы с частотой ![]() , то возникающая при движении
массы сила инерции тоже меняется по гармоническому закону
, то возникающая при движении
массы сила инерции тоже меняется по гармоническому закону ![]() . Если точка приложения возмущающей силы не совпадает с
сосредоточенной массой (рис. 1), то, пренебрегая силами сопротивления,
амплитудное значение силы инерции можно найти по формуле
. Если точка приложения возмущающей силы не совпадает с
сосредоточенной массой (рис. 1), то, пренебрегая силами сопротивления,
амплитудное значение силы инерции можно найти по формуле
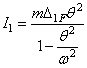 ,
(2)
,
(2)
где ![]() – статическое
перемещение сечения, в котором расположена сосредоточенная масса, по
направлению ее возможного движения, вызванное амплитудным значением заданной
нагрузки
– статическое
перемещение сечения, в котором расположена сосредоточенная масса, по
направлению ее возможного движения, вызванное амплитудным значением заданной
нагрузки ![]() . Это перемещение ищется, как правило, по методу Максвелла –
Мора. Из формулы (2) видно, что, когда частота собственных колебаний
. Это перемещение ищется, как правило, по методу Максвелла –
Мора. Из формулы (2) видно, что, когда частота собственных колебаний ![]() равна частоте
вынужденных колебаний
равна частоте
вынужденных колебаний ![]() , амплитуда силы инерции (а стало быть
и амплитуда перемещения массы) стремится к бесконечности. Это известное в
физике явление называется резонансом.
, амплитуда силы инерции (а стало быть
и амплитуда перемещения массы) стремится к бесконечности. Это известное в
физике явление называется резонансом.
Предполагаем, что частота вынужденных колебаний достаточно далека от частоты собственных колебаний и система работает упруго. В этом случае максимальное значение изгибающего момента (изгибающего момента от динамического действия нагрузки) можно найти, используя принцип независимости действия сил,
![]() . (3)
. (3)
Формула (3)
показывает, что изгибающий момент от динамического действия нагрузки ![]() равен сумме момента,
вызванного статическим действием амплитуды возмущающей нагрузки
равен сумме момента,
вызванного статическим действием амплитуды возмущающей нагрузки ![]() , и момента от амплитудного значения силы инерции
, и момента от амплитудного значения силы инерции ![]() . (
. (![]() – изгибающий момент от единичной силы, приложенной в
сечении, где расположена масса, и направленной по направлению ее возможного
движения). Напряжения в конструкции от динамического действия нагрузки меняются
пропорционально величине внутренних усилий.
– изгибающий момент от единичной силы, приложенной в
сечении, где расположена масса, и направленной по направлению ее возможного
движения). Напряжения в конструкции от динамического действия нагрузки меняются
пропорционально величине внутренних усилий.
Примечание. В частном, наиболее часто
встречающемся случае, когда точка расположения массы и точка приложения
динамической нагрузки совпадают, ![]() и
и ![]() . Тогда динамические усилия можно определить через
статические усилия и динамический коэффициент
. Тогда динамические усилия можно определить через
статические усилия и динамический коэффициент ![]() :
:
![]() , где
, где 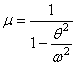 .
.
Решение.
Найдем частоту
свободных колебаний по формуле 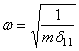 . Перемещение
. Перемещение ![]() ищем методом Максвелла
– Мора
ищем методом Максвелла
– Мора
![]() .
.
Для построения
эпюры изгибающих моментов ![]() приложим в точке, где
расположена сосредоточенная масса, единичную силу по направлению возможного
перемещения массы. В данном примере сосредоточенная масса может перемещаться
только по вертикали и эпюра моментов от единичной силы показана на
рис. 3, а. Интегрирование
формулы Максвелла – Мора по правилу Верещагина дает:
приложим в точке, где
расположена сосредоточенная масса, единичную силу по направлению возможного
перемещения массы. В данном примере сосредоточенная масса может перемещаться
только по вертикали и эпюра моментов от единичной силы показана на
рис. 3, а. Интегрирование
формулы Максвелла – Мора по правилу Верещагина дает:
![]()
![]() .
.

Рис.3
Обратите
внимание на единицы измерения величины ![]() . Подставим
. Подставим ![]() в формулу
в формулу 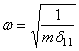 . Вспомним, что 1 кН = 103 Н = 103 кгм /сек2,
после подстановки массы
. Вспомним, что 1 кН = 103 Н = 103 кгм /сек2,
после подстановки массы ![]() в "кг" получим круговую частоту
свободных колебаний в "сек–1":
в "кг" получим круговую частоту
свободных колебаний в "сек–1":
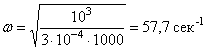 .
.
Теперь
определим амплитудное значение силы инерции, используя формулу 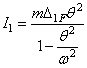 . Чтобы воспользоваться этой формулой
найдем величину
. Чтобы воспользоваться этой формулой
найдем величину ![]() – перемещения по
направлению движения массы от амплитудного значения силы
– перемещения по
направлению движения массы от амплитудного значения силы ![]() . В соответствии с методом Максвелла – Мора это перемещение
. В соответствии с методом Максвелла – Мора это перемещение
![]() .
.
Эпюра ![]() от действия
амплитудного значения
от действия
амплитудного значения ![]() показана на
рис. 3, б. Перемножая эпюры
показана на
рис. 3, б. Перемножая эпюры ![]() и
и ![]() по правилу Верещагина
найдем
по правилу Верещагина
найдем
![]()
![]() .
.
Частота вынужденных колебаний согласно условию
![]() .
.
Тогда
амплитудное значение силы инерции по формуле 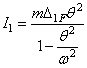
![]() .
.
Окончательная
эпюра изгибающих моментов от динамического действия нагрузки, построенная с
учетом формулы ![]() , показана на
рис. 4.
, показана на
рис. 4.

Рис.4
Пример 13.
Электромотор весом Q =
80 кН установлен на стальной балке (рис.12) из двух двутавров
№20 ГОСТ 8239-72 ![]() , один конец которой закреплен на шарнирно неподвижной опоре,
а другой на металлическом стержне длиной LS = 1,6 м
круглого поперечного сечения диаметром
, один конец которой закреплен на шарнирно неподвижной опоре,
а другой на металлическом стержне длиной LS = 1,6 м
круглого поперечного сечения диаметром ![]() м. Длина балки L =
2 м. Частота вращения ротора мотора n = 600 об/мин., вес неуравновешенных
частей Р
=1,6 кН, их эксцентриситет t = 0,02 м.
Модуль упругости стали
м. Длина балки L =
2 м. Частота вращения ротора мотора n = 600 об/мин., вес неуравновешенных
частей Р
=1,6 кН, их эксцентриситет t = 0,02 м.
Модуль упругости стали ![]() МПа.
МПа.
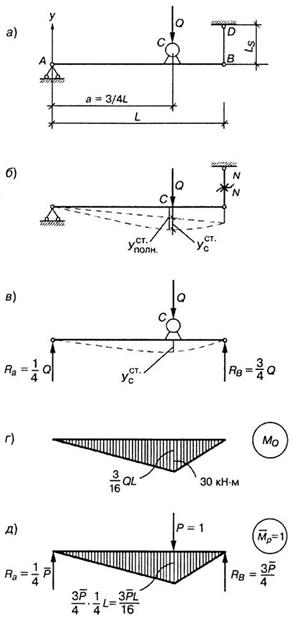
Рис. 1
Пренебрегая массой балки и внутренним трением, требуется определить:
1) Статическое удлинение опорного стержня.
2) Статическое перемещение и статическое напряжение в сечении балки, где находится электромотор.
3) Частоту собственных и вынужденных колебаний системы.
4) Коэффициент нарастания колебаний в случае жесткого опирания балки и упругого.
5) Наибольшие динамические прогибы и динамическое напряжение в опасном сечении.
6) Проверить
прочность сечения балки из 2-х двутавров (ГОСТ 8239-72) при допускаемом
напряжении ![]() .
.
Решение.
1) Определение статического удлинения опорного стержня, статического прогиба и статического напряжения в сечении «С» балки
Из уравнений
равновесия статики (рис.1,в) ![]() и
и ![]() найдем опорные реакции в балке АВ.
найдем опорные реакции в балке АВ.
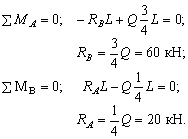
Найдем вертикальное перемещение опоры В за счет удлинения подвески при растяжении (рис.1, б). Конец балки В переместится на величину
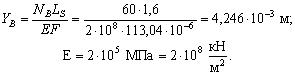
Площадь подвески
![]() .
.
Определим статический прогиб в точке «С» балки АВ при условии, что опора В является жесткой.
Используя
правило Верещагина (рис.1, г,д), найдем перемещение в сечении «С» ![]()
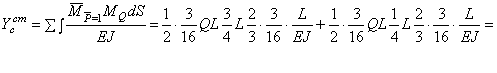
![]()
Статическое напряжение в сечении «С» балки
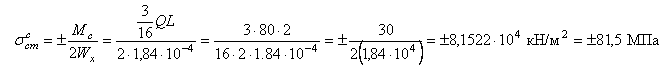
Вычислим величину полного перемещения «С» балки при учете удлинения правой подвески по формуле
![]()
2) Определение частоты собственных и вынужденных колебаний системы, коэффициента нарастания колебаний, наибольшего динамического прогиба и динамического напряжения в опасном сечении «С»
Находим частоту собственных колебаний:
- при жестком опирании
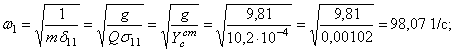
- при упругом опирании
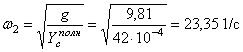 .
.
Вертикальная составляющая центробежной силы вызывает поперечные колебания балки в вертикальной плоскости с частотой возмущающей силы
![]()
Находим коэффициент нарастания колебаний
- при жестком опирании
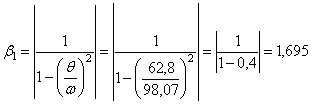 ;
;
- при упругом опирании
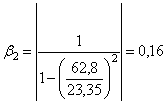 .
.
Амплитудное значение инерционной силы
![]() .
.
Коэффициент
динамичности:
- при жестком опирании
![]()
- при упругом опирании
![]()
3) Вычислим динамические напряжения при жестком и упругом опирании
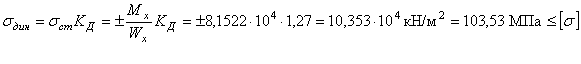
![]()
Максимальный
динамический прогиб:
при жестком опирании опоры В
![]()
при упругом опирании
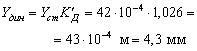
При упругом опирании динамические напряжения снижаются на
![]()
Следует учесть, что при разгоне ротора от нуля до расчетной частоты в системе с упругим опиранием будет пройден резонанс, а с жестким – система не дойдет до резонанса. Поэтому в нашем случае упругое опирание более опасно. Для того, чтобы избежать резонанса в случае упругого опирания частота вращения ротора электромотора должна быть уменьшена
![]() .
.
Напишем закон
изменения во времени прогиба балки в месте, где находится электромотор при
условии установившихся колебаний 
- при жестком опирании

- при упругом опирании

Период
вынужденных колебаний ![]() .
.
Вычисления проводим в табличной форме
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1,02 |
0 |
4,2 |
|
0,025 |
1 |
0,272 |
1,297 |
-0,0258 |
4,091 |
|
0,05 |
0 |
0 |
1,02 |
0 |
4,2 |
|
0,075 |
-1 |
-0,272 |
0,742 |
0,0258 |
4,308 |
|
0,1 |
0 |
0 |
1,02 |
0 |
4,2 |
Графики
функций ![]() и
и ![]() показаны на рис.2.
показаны на рис.2.
Напишем закон изменения во времени максимального напряжения при изгибе балки в сечении С формула
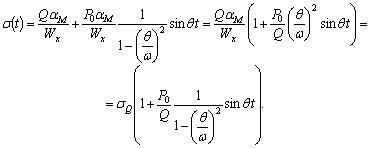
- при жестком опирании
![]()
- при упругом опирании
![]()
Вычисления проводим в табличной форме
|
|
|
|
|
|
|
|
0 |
0 |
0 |
81,5 |
0 |
81,5 |
|
0,025 |
1 |
0,272 |
103,6 |
-0,0258 |
79,4 |
|
0,05 |
0 |
0 |
81,5 |
0 |
81,5 |
|
0,075 |
-1 |
-0,272 |
59,3 |
0,0258 |
83,6 |
|
0,1 |
0 |
0 |
81,5 |
0 |
81,5 |
Графики
функций ![]() и
и ![]() показаны на рис.3.
показаны на рис.3.
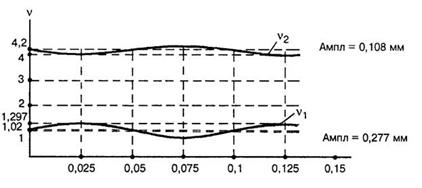
Рис. 2
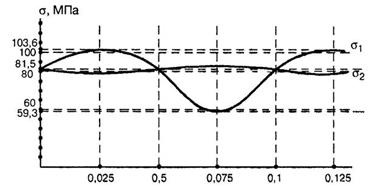
Рис. 3
Пример 14.
1. Определить собственные частоты и формы колебаний упругой балки с двумя сосредоточенными массами (рис.1).
2. Определить
амплитуды вынужденных колебаний под действием
силы ![]() , приложенной в точке А.
, приложенной в точке А.
3. Построить
эпюры динамических изгибающих моментов при ![]()

Рис.1
Решение.
В случае
плоских колебаний рассматриваемая упругая система имеет две степени свободы.
Единичные перемещения![]() определяется по правилу Верещагина, перемножая
соответствующие эпюры единичных изгибающих моментов (рис.2, б)
определяется по правилу Верещагина, перемножая
соответствующие эпюры единичных изгибающих моментов (рис.2, б)
![]()
![]()
Используя
формулу ![]() , находим собственные частоты
, находим собственные частоты
![]()
Определяем
далее собственные формы колебаний, подставляя ![]() и
и ![]() в выражение
в выражение
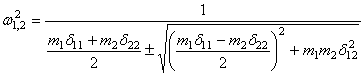 .
.
В результате для собственной формы
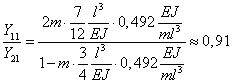
или ![]() а для второй
а для второй ![]() .
.
Используя ![]() , убедимся, что полученные собственные формы обладают свойством ортогональности:
, убедимся, что полученные собственные формы обладают свойством ортогональности:
![]()
Для определения амплитуд колебаний воспользуемся решением системы
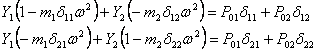 (1)
(1)
при ![]()
Тогда
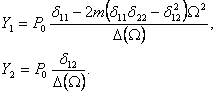 ( 2)
( 2)
Здесь ![]() - определитель
системы (1), описываемый выражением
- определитель
системы (1), описываемый выражением
![]() , если в
последнем принять
, если в
последнем принять ![]() . Нетрудно
видеть, что при
. Нетрудно
видеть, что при
![]() (3)
(3)
числитель в
выражении для ![]() обращается в нуль. На
этом основан принцип динамического
гасителя колебаний. При заданной частоте
обращается в нуль. На
этом основан принцип динамического
гасителя колебаний. При заданной частоте ![]() амплитуды
перемещений и сил ,
действующих на массы определяются
следующими выражениями :
амплитуды
перемещений и сил ,
действующих на массы определяются
следующими выражениями :
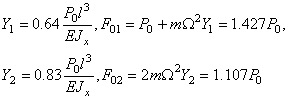
Эпюра динамических моментов представлена на рис.2.

Рис.2
Пример 15.
Определить
частоту ![]() собственных
колебаний массы m рамы
(рис. 1).
собственных
колебаний массы m рамы
(рис. 1).
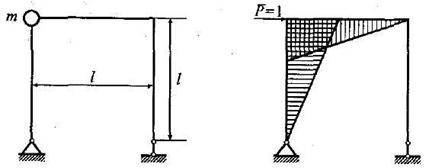
а)
б)
Рис. 1
Решение.
Система обладает одной степенью свободы, так как масса имеет возможность перемещаться только в горизонтальном направлении. Частоту собственных колебаний определяем по формуле
![]() (1)
(1)
Для
определения ![]() строим эпюру моментов
от единичной силы
строим эпюру моментов
от единичной силы ![]() приложенной к массе в
горизонтальном направлении и вычисляем
приложенной к массе в
горизонтальном направлении и вычисляем ![]() графоаналитическим способом по формуле Мора:
графоаналитическим способом по формуле Мора:
![]() (2)
(2)
Подставляя (2) в (1), найдем:
![]() (3)
(3)
Пример 16.
Определить
частоту собственных крутильных колебаний вала длиной ![]() с диском массы m на конце (рис. 1, а).
с диском массы m на конце (рис. 1, а).
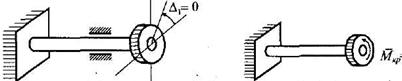
а)
б)
Рис. 1
Решение.
Положение
системы можно определить одним числом, углом поворота диска ![]() Следовательно,
система обладает одной степенью свободы.
Следовательно,
система обладает одной степенью свободы.
Согласно 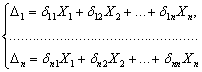 имеем:
имеем:
![]() (1)
(1)
Сила ![]() в данном случае есть
момент инерции системы:
в данном случае есть
момент инерции системы:
![]() (2)
(2)
где
![]() момент инерции диска массой m и радиуса R.
момент инерции диска массой m и радиуса R.
На основании (2) уравнение (1) принимает вид:
![]()
где
![]()
Согласно рисунку (1,б) имеем:
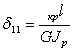
Поэтому
![]() .
.
Пример 17.
Определить частоты собственных колебаний балки с двумя сосредоточенными массами (рис. 1).

а)
б)
Рис. 1
Решение.
Для определения частот собственных колебаний имеем уравнение
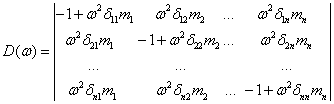 , которое
для n = 2 принимает вид:
, которое
для n = 2 принимает вид:
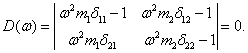 (1)
(1)
Раскрывая определитель (1), получим:
![]() (2)
(2)
На рис. 2 построены эпюры моментов от единичных сил:
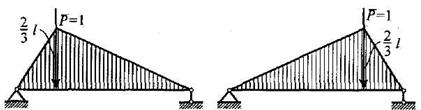
а)
б)
Рис. 2
Согласно
формуле Мора 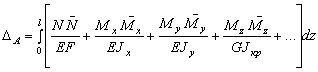 имеем:
имеем:
![]()
Если принять ![]() , то из (2) получим:
, то из (2) получим:
![]()
причем ![]() Таким образом, система имеет две собственные частоты
колебаний,
Таким образом, система имеет две собственные частоты
колебаний,
Полагая в 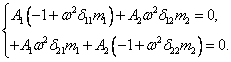
![]() , получим
, получим ![]() . Полагая
. Полагая ![]() найдем
найдем ![]() . В первом случае массы колеблются в одной фазе (рис. 1,а),
во втором случае - в противо-фазе (рис.1,б).
. В первом случае массы колеблются в одной фазе (рис. 1,а),
во втором случае - в противо-фазе (рис.1,б).
В общем случае
колебания с частотами ![]() и
и ![]() происходят одновременно. Закон движения в этом случае (каждой
массы) будет:
происходят одновременно. Закон движения в этом случае (каждой
массы) будет:
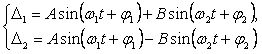 (3)
(3)
где А, В, ![]() постоянные,
определяемые из начальных условий.
постоянные,
определяемые из начальных условий.
Пример 18.
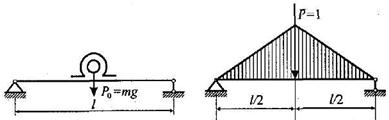
Определить
критическое число n оборотов мотора, вес которого ![]() (рис. 1, а).
(рис. 1, а).
Решение.
При критическом числе оборотов мотора имеет место резонанс, условием которого будет:
![]()
где
![]()
а) б)
Рис. 1
На основании формулы Мора и рис. 1, б, находим:
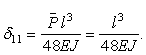
Следовательно,
![]()
Пример 19.
Определить
низшую частоту собственных колебаний балки методом Релея, если вес единицы ее
длины равен ![]() (рис. 1).
(рис. 1).
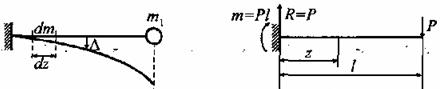
а)
б)
Рис. 1
Решение.
Найдем сначала приближенное выражение изогнутой оси балки. Для этого к концу балки приложим поперечную силу Р. Согласно методу начальных параметров, прогиб произвольной точки с координатой z будет:
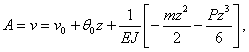
или, так как ![]() то
то
![]() (1)
(1)
Вычислим
потенциальную энергию согласно 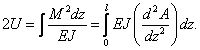 :
:
![]() (2)
(2)
Знаменатель в
формуле Релея ![]() с учётом (1) будет
равен:
с учётом (1) будет
равен:
![]() (3)
(3)
поэтому, согласно (2), (3) и формулы Релея имеем:
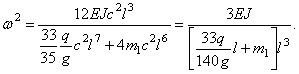
Точное решение этой же задачи есть:
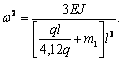
При ![]() легко подсчитать
ошибку приближённого решения. Она составляет всего 1,5%.
легко подсчитать
ошибку приближённого решения. Она составляет всего 1,5%.
Пример 20.
Определить
методом Релея низшую частоту собственных колебаний системы, состоящей из
стержня и присоединенной к ней массы m. Масса стержня равна M (рис. 1).
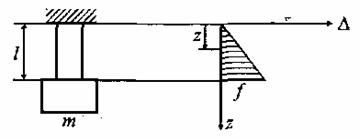
Рис. 1
Решение.
Примем для перемещения поперечного сечения стержня выражение:
![]() (1)
(1)
Согласно 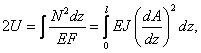 с учётом (1), получим:
с учётом (1), получим:
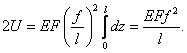 (2)
(2)
Знаменатель в
формуле Релея ![]() :
:
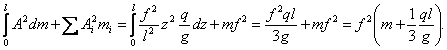 (3)
(3)
Подставляя (2) и (3) в формулу Релея, найдём:
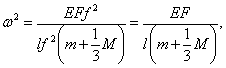
где ![]() - масса стержня.
Величина
- масса стержня.
Величина ![]() носит название
приведенной массы. Коэффициент
носит название
приведенной массы. Коэффициент ![]() - коэффициент
приведения массы. Он показывает, какую часть массы стержня нужно присоединить к
сосредоточенной массе m чтобы свести упругую систему к системе с одной степенью
свободы. Если масса стержня
- коэффициент
приведения массы. Он показывает, какую часть массы стержня нужно присоединить к
сосредоточенной массе m чтобы свести упругую систему к системе с одной степенью
свободы. Если масса стержня ![]() то
то
![]()
Пример 21.
Определить приведенную массу и частоту собственных колебаний тяжелой балки (рис. 1).

Рис. 1
Решение.
Примем для амплитуды выражение
![]()
Тогда, с
учётом ![]() имеем:
имеем:
![]()
Перемещение ![]()
Поэтому
![]()
Пример 22.
Определить
динамический прогиб и напряжения в опасных сечениях балок КD и АВ, возникающих под
действием работающего электромотора весом G = 10 кН
(рис. 1, а). Вес
неуравновешенных частей ротора Р = 1 кН.
Эксцентриситет вращающихся масс е = 0,02 м.
Число оборотов ротора n = 600 об/мин.
Массой балок в расчетах пренебречь. Поперечное сечение балок КD и АВ
состоит из двух двутавров №20 (![]() м4;
м4; ![]() м3). Модуль
упругости стали
м3). Модуль
упругости стали ![]() кН/м2.
кН/м2.
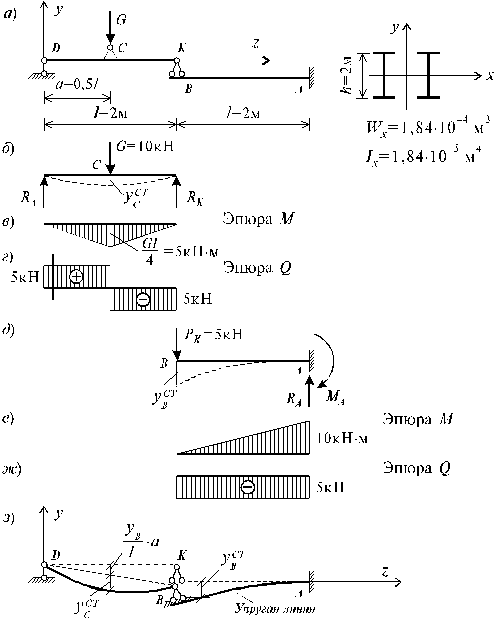
Рис. 1
Решение.
1. Определение
статического прогиба в сечении С балки КD и
статического напряжения в сечении у заделки А. Из уравнений
равновесия статики ![]() и
и ![]() найдем опорные реакции
в балке КD (рис. 8.4, б):
найдем опорные реакции
в балке КD (рис. 8.4, б):
![]() кН.
кН.
На
балку АВ в точке В (К) опоры на консоль передается нагрузка Р = 5 кН, равная по величине опорной реакции RK , но обратная по
направлению. Из уравнений ![]() и
и ![]() определяем реактивные
усилия в заделке А
балки АВ: МA = 10 кНм; RА = 5 кН. Определив
опорные реакции в балках, строим эпюры поперечных сил Q и изгибающих моментов М
для балок КD и АВ (рис. 1, в, г, е, ж). Зная величины
изгибающих моментов, возникающих в опасных сечениях балок, определяем
статические напряжения в сечениях С
и А:
определяем реактивные
усилия в заделке А
балки АВ: МA = 10 кНм; RА = 5 кН. Определив
опорные реакции в балках, строим эпюры поперечных сил Q и изгибающих моментов М
для балок КD и АВ (рис. 1, в, г, е, ж). Зная величины
изгибающих моментов, возникающих в опасных сечениях балок, определяем
статические напряжения в сечениях С
и А:
![]() кН/м2;
кН/м2;
![]() кН/м2.
кН/м2.
Для определения статического прогиба в точке С балки КD вначале предполагаем, что эта балка опирается на абсолютно жесткое основание. Используя метод начальных параметров, составляем уравнение прогибов, приняв начало координат в сечении D.
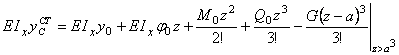 ,
,
где y0 = 0, М0
= 0, ![]() ,
, ![]() .
.
Для
нахождения ![]() составим уравнение
прогиба для сечения К
в котором прогиб равен нулю из условий закрепления:
составим уравнение
прогиба для сечения К
в котором прогиб равен нулю из условий закрепления:
![]()
Так как ![]() , то, решая это уравнение, получим:
, то, решая это уравнение, получим:
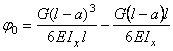 .
.
Подставив
найденное значение ![]() в уравнение прогиба
для сечения С,
получим формулу для определения
в уравнение прогиба
для сечения С,
получим формулу для определения ![]() :
:
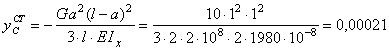 м.
м.
Для вычисления
полного перемещения сечения С с
учетом характера опирания балки КD
на консольную балку необходимо найти
прогиб консольной балки АВ от действия на нее силы РK = -RK = 5 кН.
Для этого, приняв начало координат в сечении В балки АВ, составим
уравнение метода начальных параметров для определения прогиба на конце консоли.
При начале координат в точке В консоли известными параметрами будут: М0 = МB = 0; Q0 = QB = -РK = -5 кН,
а неизвестными ![]() ;
; ![]() .
Неизвестные начальные параметры y0
и
.
Неизвестные начальные параметры y0
и ![]() определим из уравнений прогиба и угла поворота
для сечения А. Из условия
закрепления балки АВ имеем при z = l = 2 м:
определим из уравнений прогиба и угла поворота
для сечения А. Из условия
закрепления балки АВ имеем при z = l = 2 м: ![]() .
.
Составим уравнения метода начальных параметров:
![]() (1)
(1)
![]() . (2)
. (2)
Приравняв к
нулю уравнение (1) при z = l м, определяем ![]() :
:
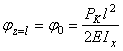 .
.
Подставив
найденное значение ![]() в уравнение (2) и
принимая y = 0 при z = l , получим выражение второго неизвестного начального
параметра y0 ,
определяющего прогиб сечения В консольной балки АВ:
в уравнение (2) и
принимая y = 0 при z = l , получим выражение второго неизвестного начального
параметра y0 ,
определяющего прогиб сечения В консольной балки АВ:
![]() ;
;
![]() ;
;
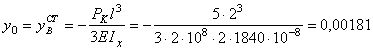 м.
м.
Знак “минус” говорит о том, что конец консольной балки переместится вниз.
Определив
прогиб ![]() и изобразив эпюру
перемещений системы (рис. 1, з),
вычислим величину полного перемещения сечения С по формуле:
и изобразив эпюру
перемещений системы (рис. 1, з),
вычислим величину полного перемещения сечения С по формуле:
![]() м.
м.
2. Определение
динамического коэффициента и коэффициента эквивалентности. Максимальное
значение системы внешних сил принимает значение ![]() . Далее определяем коэффициент эквивалентности:
. Далее определяем коэффициент эквивалентности:
![]() ,
,
где ![]() - амплитудное значение инерционной силы;
- амплитудное значение инерционной силы; ![]() - коэффициент динамичности. Здесь
- коэффициент динамичности. Здесь 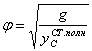 -частота
собственных колебаний;
-частота
собственных колебаний; ![]() - частота возмущающей силы.
- частота возмущающей силы.
В рассматриваемом примере:
![]()
![]() ;
; ![]()
![]() ;
;
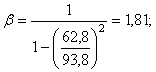
![]() кН;
кН;
![]() .
.
3. Определение прогиба и напряжений. Максимальное значение напряжения и прогиб, возникающие от совместного действия статических и динамических нагрузок, определяем по формулам:
![]() кН/м2,
кН/м2,
![]() м.
м.
При коэффициенте КД = 1,145 найдем также напряжение в сечении А балки АВ:
![]() кН/м2.
кН/м2.
Следовательно,
полученное значение напряжения больше, чем напряжение в сечении С, где установлен электромотор. Итак,
сечение в заделке в данном примере является наиболее опасным ![]() , и, следовательно, это обстоятельство необходимо учитывать
при проверке прочности составных конструкций.
, и, следовательно, это обстоятельство необходимо учитывать
при проверке прочности составных конструкций.
С увеличением
числа оборотов двигателя возрастают динамические напряжения и прогибы балок.
Поэтому при проектировании конструкций не следует допускать наступления
резонанса (![]() ), при котором может наступить разрушение конструкции.
), при котором может наступить разрушение конструкции.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов